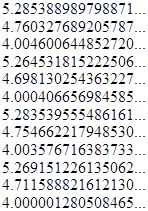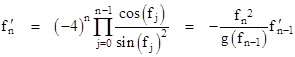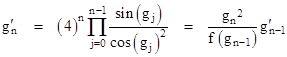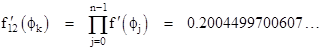The Twelve-Step Cycle of 4/sin(x)

Beginning with any real number x, the sequence of values produced by iterating the function x → -4/sin(x) invariably converges on the twelve-step cycle

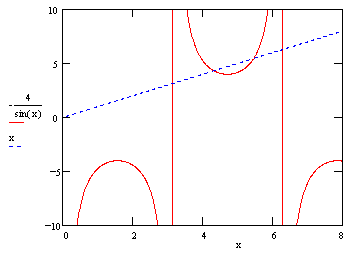
or else the cycle consisting of the negatives of these values. A plot of the basic function -4/sin(x) is shown in the figure below.

The twelve values in the cycle cluster into three sets, near the values 4.0, 4.74, and 5.28, and the general pattern of the iteration is depicted in the figure below.

Of course, the function 4/sin(x) has infinitely many fixed points and cycles, but only the above 12-step sequence is stable, so essentially any initial value converges rapidly on this cycle (or the negative of this cycle). Incidentally, the same cycle is produced by iterations of the function y → 1/[sin(y)cos(y)] by the simple change of variable x = 2y.

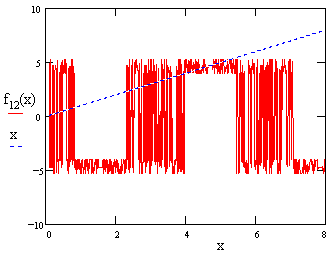
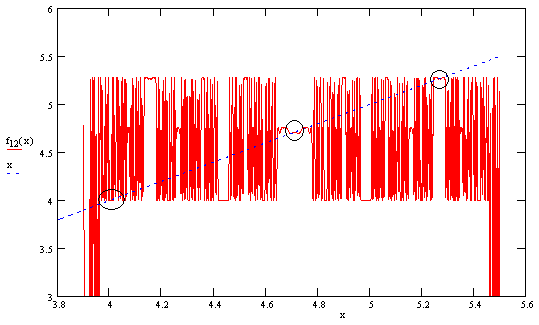
We define the function f(x) = 4/sin(x), and then let f_n(x) denote the nth iterate of f(x). (The absence of the minus sign in f(x) simply results in the convergent sequence of values having alternating signs.) It follows that the values of the asymptotic sequences (twelve of each sign) are fixed points of the function f₁₂(x), which is to say, f₁₂(x) = x for each of those 24 values of x. The figure below shows a plot of the function f₁₂(x) for positive x.

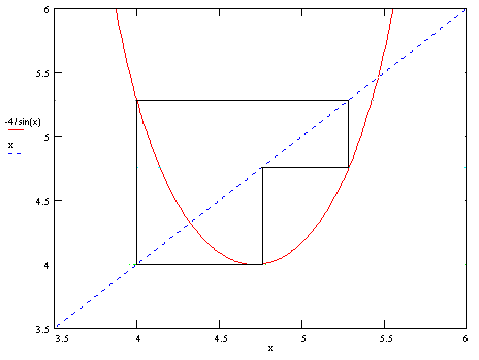
Interestingly, the three clusters of four fixed points (near 4.0, 4.74, and 5.28) occur at three similar pairs surrounding inflection points.  The figure below zooms in on the region where the stable fixed points occur.

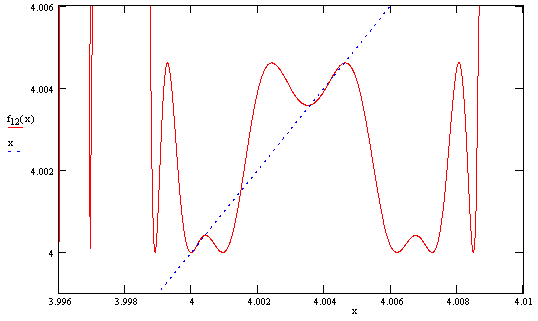
An even more magnified view of the set of four stable points near 4.0 is shown below.

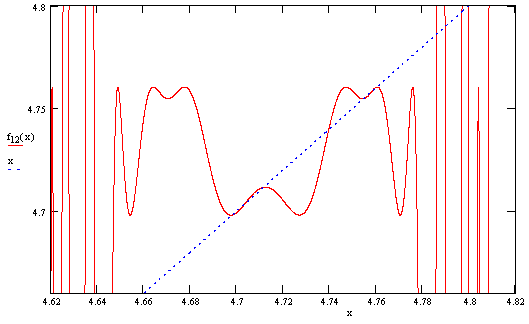
Similarly, the four stable fixed point of f(x) near 4.74 are shown below.

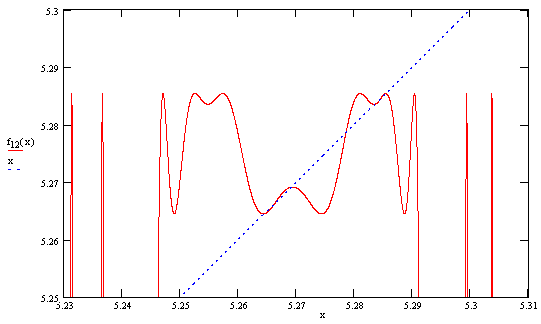
Finally, the four stable fixed points near 5.28 are shown in below,

It's interesting that such a simple function as -4/sin(x) possesses a non-trivial but unique stable limit cycle (up to sign), and that the 12-fold composition of that simple function possesses just 12 stable fixed points. (Could there be any manifestations of this cycle in nature?) The fixed points occur near local maxima or minima of f₁₂, but they actually occur at points where the slope of f₁₂ is not precisely zero. The derivative of f₁₂ has exactly the same (non-zero) value at each of the fixed points. In general the derivative of f_n can be expressed in the form of a product as follows

where we have defined g(x) = 4/cos(x). Obviously the derivatives of the iterates of g are given by the similar formula

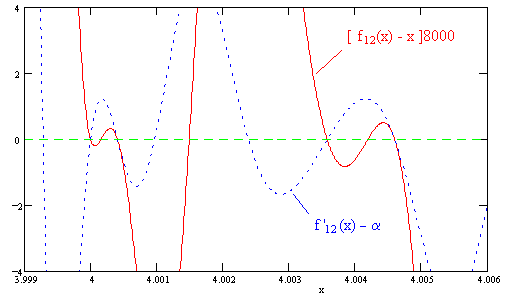
The derivative of f₁₂(x) at each of the 24 stable fixed-point values of x is exactly α = 0.20044997006… A plot showing f₁₂(x) – x superimposed on f ’₁₂(x) – α for the region near 4.0 is shown below.

The four fixed point values are where both of these curves cross zero at the same point. In between each pair of stable fixed points is another fixed point (unstable) coinciding with a maximum of the derivative function. The reason the derivative of f₁₂ has exactly the same value at all twelve fixed points (which is 24 points including signs) is obvious when we consider that the overall derivative of f₁₂(x) at any given value of x is the product of the derivatives of f(x) at the x values of x, f₁(x), f₂(x),…, f₁₁(x). Thus letting ϕ_j denote the jth value of the twelve-step cycle, we have

for every index k, because each one is given by the product of the same twelve factors, taken in a different order around the cycle.

Return to MathPages Main Menu