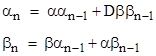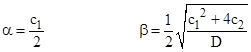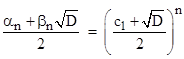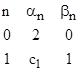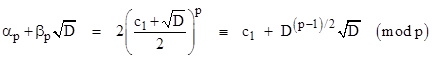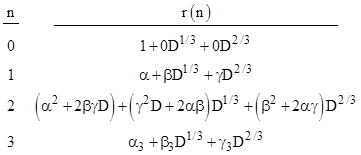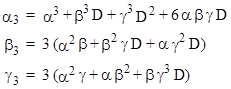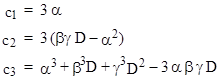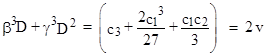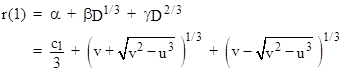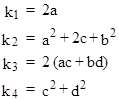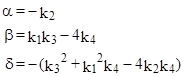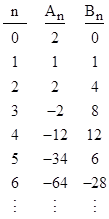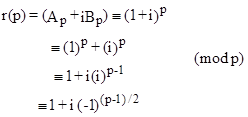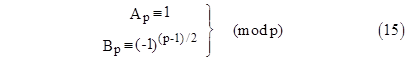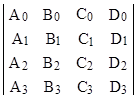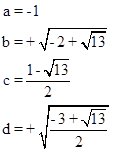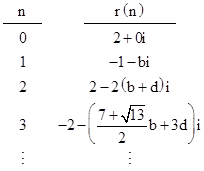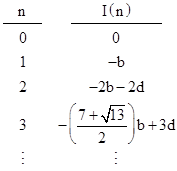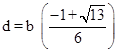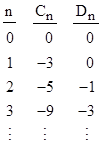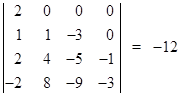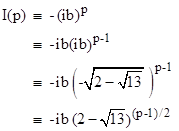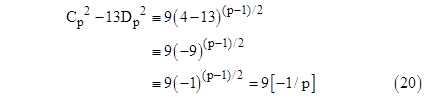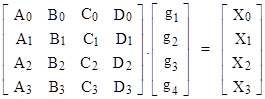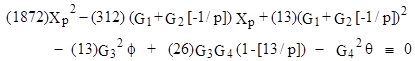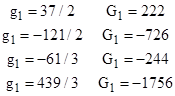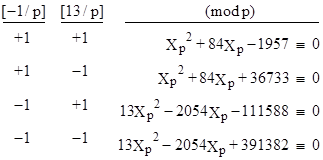3  Congruence Conditions On The Terms Of Linear Recurring Sequences

3.1  Second Order Recurrences

To determine congruence conditions on the terms of a linear recurring sequence, we must first determine a closed-form expression for the nth term using only rational functions and root extractions. Consider the second order recurrence

This recurrence corresponds to a first order recurrence of the form

where α, β, and D are constants. Let r_n denote the sum of the roots of the characteristic polynomial of (2). The initial value is r₀ = 1, and all subsequent values can be generated recursively using (2). Now we define α_n and β_n by the formal relation

from which we get

The sequences α_n and β_n each individually satisfy the second order recurrence (1), provided we take the coefficients

Setting D equal to the determinant, this implies α = c₁/2 and β = 1/2, so we have

By construction the α_n and β_n sequences are integers (assuming c₁ and c₂ are integers) with the initial values

For any prime p we have

Therefore

modulo p, where [D/p] denotes the Legendre symbol. Since the sequences A_n and B_n are linearly independent, we can now express congruence conditions on the pth element of any integer sequence that satisfies the general homogeneous recurrence relation (1). For example, the basis sequence elements satisfy the congruences

We can also determine quadratic congruence conditions on the elements b₀(m) and b₁(m) where m = (p–1)/2.

3.2  Third Order Recurrences

In the quadratic case we found that the roots of the general quadratic polynomial were given by the closed form of the linear recurrence term. In this section we show that the solution of the general cubic is given by the closed form of the third order linear recurrence.

A set of three linearly independent solutions of the recurrence

can be found by considering a first order recurrence of the form

where α,β,γ,D are real (but D^1/3 and D^2/3 are complex). Letting r(n) denote the nth power of the characteristic root of (4), we have the following initial values

where

Since the three components of each value are incomensurate, these components are each solutions of the same recurrence as the characteristic recurrence of r(n). Identifying this with the general third order recurrence (3), we have three equations in the three unknown coefficients c₁,c₂,c₃. Solving these equations gives

Therefore, we immediately have

Substituting this into the equations for β and γ leads us to define quantities u and v as follows

and

Eliminating either β or γ from these equations leads to a quadratic equation with the roots

Therefore, we have

By its construction, this is the general form of the roots of the characteristic polynomial of (1), i.e., the general cubic

3.3  Fourth Order Recurrences

Given any integer k and a sequence of integers s₀, s₁, s₂,... that satisfies a fourth order linear homogeneous recurrence relation for which the resolvant cubic of the characteristic quartic has a rational root, this section describes a method for determining the primes p such that s_p = k (mod p).

Consider the general homogeneous fourth order recurrence

To analyze this recurrence we first consider the following second order recurrence with complex coefficients

where a, b, c, and d are real. Let r(n) denote the sum of the nth powers of the roots of the characteristic polynomial of (6). The initial values are

and all subsequent r(n) can be generated using (6). If we let A_n and B_n denote, respectively, the real and imaginary coefficients of r(n), then we have

Seperating the real and imaginary components, we find that the sequences A_n and B_n each individually satisfy the fourth order recurrence (5) with the coefficients

These equations imply that a = k₁/2 and c = y/2 where y is a root of the cubic

with

Equation (7) is called the resolvant cubic of the quartic polynomial corresponding to (5). If x₁, x₂, x₃, x₄ are the roots of the characteristic equation of (5), and y₁, y₂, y₃ are the roots of (7) then

Given the value of c based on any root y of (7), the corresponding values of b and d are

with the stipulation tha..

t

This last condition relates the signs of b and d, and is a useful identity for ring multiplication to be discussed later.

Example:

To illustrate, consider the fourth order recurrence

whose characteristic polynomial

is irreducible (according to Eisenstein's criterion). For this case we have

which gives  a = –1  and

Taking the root c = –1, we can use (8) and (9) to compute b = ±1 and d = ±1. Now, since (10) gives bd = 1, it follows that b and d have the same sign. Choosing b = d = –1, equation (6) gives the second order complex-valued recurrence

with the characteristic equation

If we let r(n) = A_n + iB_n denote the sum of the nth powers of the complex roots of h(z), then we have the initial values

By their construction, both of these sequences individually satisfy the original fourth order real-valued recurrence (11) for n > 4. If s(n) denotes the sum of the nth powers of the roots of (12), then  s(n) = 2A_n.

Now, if p is an odd prime, we have  the following congruences

from which it follows that

To complete the analysis of the general fourth order recurrence we need two more solutions C_n and D_n which, together with A_n and B_n, will form a basis for all possible solutions. That is, any solution X_n of (11) will be expressible as

where the g_m are constants determined by the initial values of X_n. Any four solution sequences constitute a basis provided that they are linearly independent, for which a necessary and sufficient condition is that the determinant

is non-zero. However, our purpose is to define primality criteria for every possible X_p, which requires that we be able to define congruence conditions on C_n and D_n when n is a prime, similar to the conditions on A_n and B_n given by equations (15). Our approach will be to derive another second order complex-valued recurring sequence, different from (14), but with real and imaginary parts that also satisfy the basic fourth-order recurrence (11).

One possibility would be to use a = c = –1 as before, but choose the signs b = d = +1. However, this does not lead to independent sequences. Instead, we keep a = –1 and return to the cubic (13) for a different value of c. Factoring out the root c = –1 leaves

which has the roots (1±√13)/2. To make b and d real valued we choose the root c = (1–√13)/2, which results in the following set of coefficients

It is useful to observe that, in view of (10), we have

..

Inserting these values of a, b, c, and d into equation (6) gives a second order complex-valued recurrence with the characteristic polynomial

Again letting r(n) denote the sum of the nth powers of the roots of h(z), we have the initial values

By their construction, the real and the imaginary parts of r(n), taken seperately, both satisfy the basic fourth order recurrence (11). Clearly the real part of this r(n) is identical to the A_n sequence already discussed. Our objective is to derive two new and independent integer sequences from the imaginary part of this r(n). Letting I(n) denote the coefficient of the imaginary part of r(n), we have the initial values

As a consequence of equation (10), the irrational quantities b and d are related by

so every element of the I(n) sequence can be expressed in the form

where α_n and β_n are rational coefficients. The values of I(0) and I(1) are already of this form. The remaining initial values are

In order to deal only with integer sequences, we will work with 3I(n) instead of I(n), and we will define the two new basis sequences C_n and D_n as follows

The initial values of these sequences are

The four sequences A_n, B_n, C_n, and D_n are linearly independent, as shown by the non-zero determinant

It remains to establish congruence requirements on C_p and D_p for primes p. We know that

For the remainder of this section, all congruences are understood to be modulo p. Concerning ourselves only with the imaginary part, we have

Therefore, by equation (17) we have

and also

from which it follows that

where [–1/p] is the Legendre symbol. Furthermore, squaring congruences (18) and (19), and multiplying by (2–√13), we have

Expanding the right side using the binomial theorem, we have

and

Dividing (21) by 2, and (22) by –1, and noting that 2^p–1  = 1  and  13^(p–1)/2  = [13/p]  (Euler's criterion), we have

and

Subtracting (23) from (24) and dividing by 9 gives

Substituting this into (23) give..s

recalling equation (20)

we can solve (25) and (20) simultaneously for C_p² and 13D_p², which gives

Letting Φ and θ denote, respectively, the right sides of equations (26) and (27), we have the following complete set of basis element congruences for any prime p:

along with the condition

In view of equation (16), the residue class of X_p for any sequence of integers X that satisfies the basic recurrence (11) is given by

where the g_i may be expressed in terms of the initial values of the X sequence by solving the simultaneous equations

Since the determinant of the basis matrix is –12, and we want to deal only with integers, we multiply (29) by 12 to clear any fractional values of the g_i, and then define G_i = 12g_i . Also, to clear the radicals from (29) we can bring the first two terms on the right over to the left, and then square both sides (bearing in mind that the cross-product of radicals is an integer by equation (28)) to give a quadratic congruence condition on X_p. Since the square of the term √(θ/13) has a 13 in the denominator, we will multiply through by 13 to give the general form

Notice that if the prime p is not equal to 13, we can divide this congruence by 13 whenever θ (mod p) is divisible by 13, which it is when  [–1\p] = +1. Also, if p is not equal to 2 or 3, we may be able to divide by these factors.

To illustrate, consider the particular solution sequence X of recurrence (11) with the initial values  X₀ = 37, X₁ = 19, X₂ = 43, and X₃ = 101. The values of g_i and G_i for this sequence are

Therefore, for any prime p other than 2, 3, or 13, we have the following quadratic congruences on X_p:

..

These congruences enable us to easily determine the primes p such that X_p = y (mod p) for any integer y. For example, the only primes p that divide X_p are 109, 547, and 195691. Also, the only primes p such that X_p = 5000 (mod p) are 3 and 157560691.

Return to Table of Contents