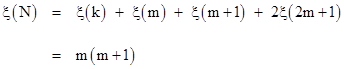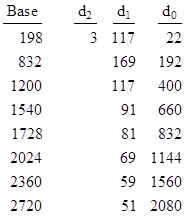|
Infinitely Many Rhondas |
|
|
|
Albert Wilansky once noted that the phone number (4937775) of his brother-in-law, Harold Smith, had the property that the sum of its decimal digits (42) is also the sum of the digits of its prime divisors (3, 5, 5, 65837). Why Wilansky was factoring his brother-in-lawís phone number in the first place is not known, but numbers with the stated property are now called Smith numbers, and have become the objects of considerable study. Of course, a prime is automatically a Smith number, but many composites are also Smith numbers. The first several are 4, 22, 27, 58, 85, 94, 121, 166, 202, 265, and so on. Clearly Smith numbers arenít particularly rare. In fact, among the positive integers less than 104 there are 1605 Smith numbers, of which 376 are composite. Since they are so plentiful, it isnít surprising that sequences of consecutive Smith numbers can be found. For example, there are eight pairs of consecutive composite Smith numbers less than 104, the smallest being 728 and 729. The smallest set of three consecutive composite Smith numbers (in the base 10) begins with 73615. (In binary, the first sequence of eight consecutive composite Smith numbers begins with 1544053.) The number 729 = 36 is also notable for being one of just ten square Smith numbers less than 105. These include some squared primes, such as 51529 = 2272. |
|
|
|
Assuming Smithís phone number was selected more or less randomly, this raises the question of how unusual it is for an arbitrarily selected integer to have some peculiar or note-worthy property. Is it possible to find an interesting property for any number? (Of course, thereís a famous paradox based on the fact that being the smallest positive integer possessing no interesting property is an interesting property.) In this regard, Iím reminded of the Rhonda Numbers. The street address of a former acquaintance of mine was 25662 W. Something, and one notices immediately that the prime factors of 25662 are 2, 3, 7, 13, and 47, the sum of which is 72, whereas the product of the decimal digits is 720, which is B times 72. Thus, we may define a Rhonda Number in the base B as an integer such that the product of the digits in base B equals B times the sum of the prime factors. The smallest example of a Rhonda number is 560 for the base 12. Thus the Rhonda numbers are quite a bit more rare than the Smith numbers. Clearly B must be composite for there to be any Rhonda Numbers to the base B, because if B is a prime, the least significant digit of the number in the base B must be zero, making the product of the digits zero. Nevertheless, despite their rarity, we can prove the following. |
|
|
|
Proposition:† There are infinitely many Rhonda Numbers. |
|
|
|
Proof:† Let ξ(n) denote the sum of the prime factors of n (including duplicate factors). Then for any integer m>5 the number N = km(m+1)(2m+1)2 is a Rhonda Number to the base B = 2km(m+1), where k is any integer such that |
|
|
|
|
|
|
|
We are assured the existence of at least one k satisfying this equation, because ξ(n) ≤ n, which implies the negative terms on the right side combined can be no larger than 6m+3, which is smaller than m(m+1) for m > 5. Therefore, the above expression for ξ(k) is a positive integer u. If u is even then u = 2s and k = 2s satisfies the equation. If u is odd, then u = 2s+3 and k = 3(2s) satisfies the equation. |
|
|
|
The digits of N in the base B are d0 = km(m+1) and d1 = 2m(m+1), so the product of these digits is 2k(m2)(m+1)2. Also, since the ξ function is additive, we have |
|
|
|
|
|
|
|
Therefore B times ξ(N) equals 2k(m2)(m+1)2, which equals the product of the base-B digits as required, completing the proof. |
|
|
|
In general, for each value of m there correspond several distinct Rhonda Numbers, one for each prime partition of ξ(k). The smallest example of a Rhonda Number given by this construction is 28392 relative to the base 336 (corresponding to m = 6 and k = 4). |
|
|
|
In this context the number 140800 has an interesting property. The digits of this number in each of several bases are shown below: |
|
|
|
|
|
|
|
In each case the product of the digits divided by the base equals 39, which also happens to be the sum of the prime factors of 140800 = (29)(52)(11). Therefore, this is a Rhonda number relative to eight distinct bases. Do there exist numbers that are Rhonda numbers to arbitrarily many bases? |
|
|