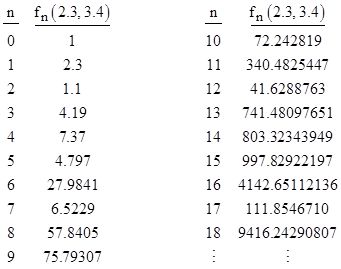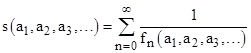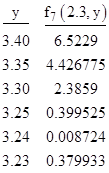|
Sequence Partitionable Into Powers of 2 or 3 |
|
|
|
Consider the minimal sequence of integers that can be "parenthesized" in two different ways, one giving the powers of 2, and the other giving the powers of 3. It's easy to see that the sequence is |
|
|
|
|
|
|
|
To give the powers of 2, we parenthesize this sequence as |
|
|
|
|
|
|
|
and to give the powers of 3 we parenthesize the sequence as |
|
|
|
|
|
|
|
Numerically the sum of the inverses of this sequence of numbers appears to converge very rapidly on the value |
|
|
|
|
|
|
|
However, itís difficult to place an upper bound on this sum, because it's possible that a sum of powers of 2 happens to be very close to a sum of powers of 3. For example, the billionth term of the sequence could be 1, which would increase the sum of inverses by 1. It even seems difficult to prove that the sum converges. |
|
|
|
In general, given two real numbers x and y, let fn(x,y) denote the nth term of the minimal sequence that can be parenthesized both as powers of x and as powers of y. For example |
|
|
|
|
|
|
|
The definition could also be expanded to include series that can be partitioned in 3 or more ways.† In other words, we can define the infinite series fn(a1,a2,a3,...) as the minimal series that can be partitioned as powers of a1, powers of a2, and powers of a3, and so on. Then we can consider the sum of the inverses of the values of such a sequence, i.e., the sum |
|
|
|
|
|
|
|
It seems difficult to evaluate this sum, or even to be sure it converges. For example, notice that† f7(2.3, 3.4) equals 6.5229, but relatively small changes in the second argument can force this term to zero, as shown by the values tabulated below |
|
|
|
|
|
|
|
Thus, although it appears that s(2.3, 3.4) converges, it is very close to a sum, s(2.3, 3.24...), whose 7th term "blows up" to infinity. Moreover, the 12th term blows up even closer, near s(2.3, 3.35...). The local sensitivity of some of the fn(x,y) to changes in x and y is exponentially dependent on n. This raises several interesting questions, such as:† What is the density of convergent (and non-convergent) points (x,y)? How far from any given (x,y) is the nearest divergent point? Does s(x,y) posses derivatives? |
|
|
|
Another interesting question is: How should we treat cases when x and/or y are less than 1? In such cases the infinite sequence eventually becomes devoted entirely to powers of the lesser of x and y, until all infinitely many of those have been "exhausted", at which time the powers of the other argument (presumably) appear. Thus, as n goes to infinity the sum approaches a certain value, but for all the terms it approaches another value, because there are two "concurrent" infinite sequences in the total sequence. It's also interesting to consider s(e,π), which appears to converge on the value 4.42122300... |
|
|