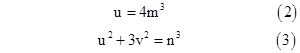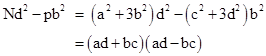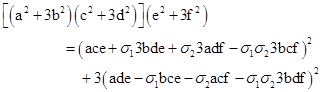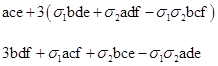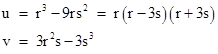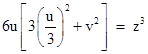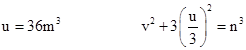Fermat's Last Theorem for Cubes

Before considering the integer equation x³ + y³ = z³, it's worthwhile to briefly review the simple Pythagorean equation x² + y² = z². For primitive solutions we can assume x,y,z are pairwise co-prime, x is odd and y is even. The usual approach is to re-write the equation as

Then, since the two integer factors on the right are co-prime (and since we have unique factorization for integers), they must each individually be squares, so we have z+x = 2u² and z-x = 2v² for co-prime integers u,v, (one odd and one even) from which it follows that z = u² + v², x = u² - v², and y = 2uv.

However, there is another approach to solving the Pythagorean equation that makes use of some deeper properties of integers known to Fermat, and that can be generalized to the case of cubes. This alternative approach relies on the fact that numbers of the form X² + Y² with gcd(X,Y)=1 can be "factored" uniquely into a product of primes of the same form, and that the representations of composites of this form are generated by applying the identity

It's been speculated that Diophantus knew this identity, although he didn't give it explicitly in any of the (surviving) books of "Arithmetica". The first known explicit description was by Abu Jafar al-Khazin (circa 950 AD), and it also appears in Fibonacci's "Liber Quadratorum" (1225 AD). One could argue that this was really the first discovery of complex numbers, in the abstract sense of Hamilton's ordered pairs, because in C the product of (a,b) and (c,d) is (ac-bd,ad+bc). In any case, Fermat knew that only primes of the form 4k+1 are expressible as a sum of two co-prime squares, and those are expressible in only one way. This, combined with the fact that representations of composites are given by the above formula applied to the representations of their factors, enables us to say that if x² + y² is a square then the components x,y are given by squaring a number of the form (u² + v²) using the above identity. As a result we have

which of course agrees with our previous solution. Thus, given the theorems about sums of two squares and their unique factorizations that were known to Fermat, this is (arguably) an even more direct solution than the original one, which is perhaps not surprising, since it is essentially employing the field of Gaussian integers, in disguised form.

Now let's consider the analogous equation for cubes, i.e., we seek all non-trivial integer solutions of x³ + y³ = z³. Again we consider only primitive solutions, so without loss of generality we can assume x,y,z are co-prime, one even and two odd. Changing signs if necessary we can make x and y odd and z even. Now we define x=u+v and y=u-v where (u,v)=1, and u,v have opposite parity. Substituting into x³ + y³ = z³ gives

Since z is even, u must be even and v must be odd. Now we'll consider two cases. First, assume z is not divisible by 3. In this case 2u is co-prime to u² + 3v², so both of those factors must be cubes. Thus we have integers co-prime m,n such that

In the case of the Pythagorean equation we had a sum of two squares equal to a square, whereas in this case we have a slightly different quadratic form, X² + 3Y², equal to a cube. Notice that we can't simply subtract u² from both sides of (3) and then factor the right hand side, because it is inhomogeneous, i.e., we would have a cube minus a square, which doesn't factor algebraically over the integers. We can, however, proceed to use the second approach, based on factoring the left hand side of (3) into divisors of the same form, provided we know enough about numbers of the form X² + 3Y².

Happily, it turns out that we have a direct analog for the "Fibonacci identity". In fact, for any integer N we have

so we can always multiply together two numbers of the quadratic form X² + NY² to give another number of the same form. With k=3 this identity is

With this identity in mind, we state and prove several facts about numbers of the quadratic form X² + 3Y² which are useful for continuing our search for solutions of x³ + y³ = z³.

LEMMA 1: Every prime p of the form 3k+1 divides some integer of the form a² + 3b² with (a,b)=1.

PROOF: Since u² + uv + v² is an equivalent form under the substitution u=b+a and v=b-a, we need only prove that p divides such an integer, with (u,v)=1. Consider

where 3k = p-1. Setting v=1 ensures (u,v)=1 and enables us to write

The left hand side is divisible by p according to Fermat's Little Theorem for any integer u co-prime to p. Therefore, the right side is also divisible by p for every such u. In order for p to NOT divide any of the number u^2k + u^k + 1, it must divide each of the numbers u^k - 1 for u = 1,2,3,..,p-1. However, the congruence u^(p-1)/3 = 1 (mod p) can have no more than (p-1)/3 distinct roots, so it is not satisfied for 2/3 of the residues modulo p. Therefore, each of those non-roots is a value of u for which p must divide u^2k + u^k + 1. Also, since more than half of those residues qualify, we can choose an odd u, and then a = (u-1)/2 and b = (u+1)/2. With these values, p divides a² + 3b², which completes the proof of Lemma 1.

LEMMA 2: If N is an integer of the form a² + 3b², and if the prime p = c² + 3d² divides N, then there exist integers u,v such that N/p = u² + 3v² and the representation of N is given by evaluating the product (p)(N/p) = (u² + 3v²)(c² + 3d²) using Fibonacci's formula.

PROOF: Since p divides N, it must divide Nd² - pb². Also, we have

which shows that the prime p must divide either ad+bc or ad-bc. Now, we can also write

Depending on whether p divides ad+bc or ad-bc, we can choose the sign in the above expression so that p divides the right-most term. Then, since it also divides Np, it must divide the first term on the right. Therefore, dividing the above expression for Np by p², we have N/p = u² + 3v² where u,v are the integers given by

again with the choice of sign such that p divides ad-+bc. Solving these two equations for a and b gives

This shows that the representation of N is given by applying Fibonacci's formula to multiply (p)(N/p), which completes the proof of Lemma 2.

LEMMA 3: If we let [n\p] equal +1 or -1 accordingly as n is or is not a square (mod p), and if m,n are residues co-prime to p, then [mn\p] = [m\p][n\p].

PROOF: If m,n are both squares (mod p), then obviously mn is also a square. Also, if one of m,n is a square and the other is not, then it follows that their product mn is not, because if m=x² and mn=y² we would have n = (y/x)², contrary to assumption that n is not square. The leaves only the case when neither m nor n is a square. To resolve this case, note that the non-zero multiplication table (modulo p) has unique inverse, so each non-zero residue appears in row and column precisely once. Also, since x²=y² (mod p) implies (x-y)(x+y) mod p, it's clear that the squares of the residues 1 through (p-1)/2 are all distinct, and respectively equal to the squares of the residues (p+1)/2 to p-1. Therefore, the squares and non-squares each make up exactly half the non-zero residues. Also, each residue appears p-1 times in the table, so if fill in all the products of two squares, and all the products of a square and a non-square, we are left only with squares, which must be placed in the remaining openings, the products of two non-squares. Therefore [mn\p] = [m\p][n\p], completing the proof of Lemma 3.

LEMMA 4: If the integer N is representable in the form a² + 3b² with (a,3b)=1, then the only odd prime factors of N are of the form p = 3k+1.

PROOF: If N was divisible by a prime p, then we have a² = -3b² (mod p), which implies that (-3) is a square modulo p. It's easy to show that [-1\p] = (-1)^(p-1)/2, and by quadratic reciprocity we also have [3\p] = [p\3](-1)^(p-1)/2. From Lemma 3 and quadratic reciprocity it follows that [-3\p] = [-1\p][3\p] = [p\3]. Thus any number of the form a² + 3b² with (a,3b)=1 is divisible by only primes of the form 3k+1, which completes the proof of Lemma 4.

Notes:

1. It's possible to avoid the use of full quadratic reciprocity here, but I wonder if Fermat might have just assumed it?

2. If a² + 3b² with (a,b)=1 is even, then a,b are odd, in which case either a+b or a-b must be divisible by 4. With that choice of sign we can set B=a±b and A=∓3b and then we have A² + 3B² = [a²+3b²]/4. Repeating if necessary, we can factor out all powers of 2, leaving an odd proper representation.

LEMMA 5: Every prime p of the form 3k+1 is expressible in the form u² + 3v² with (a,b)=1 in precisely one way.

PROOF: By Lemma 1 we know that p divides some integer of the form a² + 3b². Also, by replacing a and b with their least magnitude residues modulo p, the result is still divisible by p, but now we are assured that a and b are each less than or equal to (p-1)/2, from which it follows that a² + 3b² is strictly less than p². Therefore, all the prime divisors of a² + 3b² other than p are strictly smaller than p, and according to Lemma 4 all of those prime divisors are of the form 3k+1, and according to Lemma 3 they are all of the form u² + 3v². Therefore, we can apply Lemma 2 to each of these smaller prime divisors in turn, yielding a unique quotient of the form a² + 3b², until arriving at p. This completes the proof of Lemma 5.

LEMMA 6: The general primitive solution in integers of the equation x² + 3y² = N³ for odd N is given by x = u(u² - 9v²) and y = 3v(u² - v²) where u,v are co-prime integers.

PROOF: By Lemma 4 we know that N³ is a product of primes of the form 3k+1, each of which by Lemma 5 has a unique proper representation of the form a² + 3b². Hence by Lemma 2 we can factor x² + 3y² uniquely into a product of primes of this form, and the representation of N³ is given by applying the Fibonacci product formula. Also, it's easy to verify that Fibonacci multiplication is commutative, in the sense that the two representations given by AB are the same as the two given by BA. Also, we can verify that Fibonacci multiplication is associative, i.e., (AB)C = A(BC), by noting the results

where σ₁ and σ₂ are signed units (+1 or -1) according to our choices of signs in the two applications of the Fibonacci identity. Since both components are squared, we need consider only the magnitudes of the components, so we can multiply each term of the second component by σ₁σ₂ and write the two components as shown below

Notice that the rows transpose (a,b), (c,d), and (e,f), so they have the same symmetry, and if we define σ₃ = -σ₁σ₂ we have the three-way symmetry

Consequently, the set of proper representations given by the Fibonacci product of three proper representations is the same, regardless of the order in which the product is evaluated.

Furthermore, the number of distinct proper representations of a number equals 2^k-1 where k is the number of distinct prime divisors, because we have two proper choices of sign when multiplying two distinct factors (whereas we have no proper choices when multiplying powers of a single prime). Since the number of distinct prime divisors of N is the same as the number of distinct prime divisors of N³, we can produce all 2^k representations of N³ as the cubes of the 2^k representations of N. Thus, for some co-prime integers u,v we have not only

but also expanding the left side by the Fibonacci formula (which gives a unique proper result when cubing a single representation) we have

completing the proof of Lemma 6.

Now (finally!) we can return to our original problem. Recall that on the assumption of the existence of integers x,y,z such that x³ + y³ = z³, and assuming first that z is not divisible by 3, we had shown (see equations 2 and 3) the existence of integers m,n and co-prime integers u,v such that

where n is odd. It follows from Lemma 6 that u and v can be expressed in terms of integers r,s as follows

Also, since v is odd and u is even, we must have r even and s odd. Further, since u = 4m³, it's clear that r is 4 times a cube, and both r-3s and r+3s are cubes. Thus we have

and therefore from 2r = (r-3s) + (r+3s) we have

which is a solution of the original equation in strictly smaller integers. However, by applying the same argument to this new solution we can construct a strictly smaller solution, and so on, ad infinitum. This is clearly impossible, since there must be some absolutely smallest integer solution. Consequently, by Fermat's principle of infinite descent, we see that solutions with z not divisible by 3 are impossible.

For the second case, suppose z is a multiple of 3. It follows that u is a multiple of 3, and v is not. In this case we cannot say that 2u is co-prime to u² + 3v², because both are divisible by 3, but if we factor a 3 out of the quantity in parentheses in (1) we have

so now 6u is co-prime to the quantity in brackets, and so both factors are cubes, which implies

From Lemma 6 we have co-prime integers r,s with s even, such that

which implies

so we have

and therefore

Since 2s + (r-s) = (r+s) we have

so again we have a solution in smaller integers, and by the principle of infinite descent, this is impossible. Consequently, we have proven the result

THEOREM: The equation x³ + y³ = z³ has no solution in non-zero integers.

Return to MathPages Main Menu