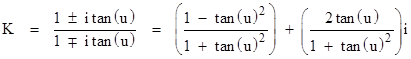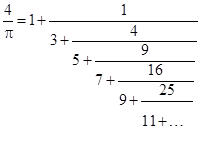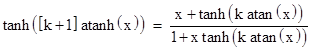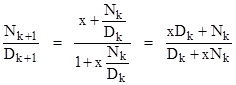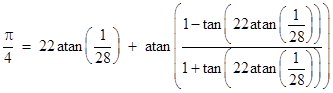Tangents, Exponentials, and π

Given the value of tan(u) for any real number u, we can compute tan(Nu) recursively using the addition rule for tangents

Thus tan(Nu) is the Nth composition of the linear fractional transformation f(z) = (az+b)/(cz+d) with the initial value z₀ = 0 and the coefficients a = 1, b = tan(u), c = −tan(u), and d = 1. Using the formulas presented in the section Linear Fractional Transformations, we have the parameters

and

This shows that |K| = 1, and it makes an angle ϕ relative to the positive real axis in the complex plane, where

Setting ϕ = 2u, we can write K in exponential form as K = e^2ui. Therefore, using the closed-form expression for the Nth composition of f(z) as explained in the section on Linear Fractional Transformations, we can write

Setting Nu = x and solving for e^2xi gives identity

so we have

In particular, since tan(π/4) = 1, we can set x = π/4 in this equation to give

Noting the identity (i-1)/(i+1) = i, this implies π = −2i ln(i), which shows iπ = 2ln(i) = ln(i²), and therefore we have Euler's celebrated identity

In addition, using the continued fraction for the natural log, we arrive at an interesting expression

Another approach to tangent additions can be most easily introduced in terms of the hyperbolic tangent, tanh(x), which has the addition rule

where we can put A = atanh(x) and B = atanh(y). Thus we have

This gives the sequence

and so on. It's easy to see that the numerator and denominator of the kth expression consist of the odd and even terms (respectively) of the expansion of (1+x)^k. To prove this, note that we begin with numerator N₁ and denominator D₁ such that (N₁ + D₁) = (1+x)¹, and also note that N₁ contains the odd powers of x and D₁ contains the even powers of x. Then notice that N_k+1/D_k+1 equals

Therefore, setting

we see that

Also, we see that N_k+1 contains all and only the odd terms of (1+x)^(k+1), and D_k+1 contains all and only the terms of the binomial expansion with even exponents, so the result is proven. (We might also mention that in the ring of polynomials with integer coefficients, since the sum of numerator and denominator is a power of (1+x), it's clear that if they had a common factor it would have to divide their sum, so it would have to be some power of (1+x), which obviously couldn’t give pure odd or pure even powers of x. Thus the numerator and denominator are coprime over the polynomials.)

The same proof can be carried through for the tangent function by using N_k(ix) − iD_k(ix) = (1+x)^k. This gives the same terms for the numerator and denominator, but with alternating signs. For example, with k = 4 we have

With this we can describe a simple approach to developing Machin-like formulas for computing π. Beginning with the tangent addition rule

set u = π/4, and take the inverse tangent of both sides to give the identity

which is valid for any v. For the most rapid convergence of the arc tangent series we want to make the quantity in parentheses very small, which we can do by setting v close to π/4. For example, based on the continued fraction convergent 22/7, we might set v = 22atan(1/28), which gives

The leading term on the right side is (3.141521..)/4, so even if we neglect the second term entirely, and evaluate the arctangent of 1/28 using the series expansion, we can arrive at a significantly better approximation than the original convergent 22/7 = 3.1428... However, in order to get more than five significant digits we need to evaluate the second term. The argument of the arctan is so small that we can very closely approximate the arctan by the argument itself, so essentially we just need to evaluate tan(22 atan(1/28)), for which we can use the "binomial formula" described above. We have

From this we get the Machin-like formula

The argument of the right hand term is just 0.000017684452323... whereas the arctangent of this is 0.000017684452321..., which differs only in the 15th digit past the decimal point. Thus by simply using the argument we can compute π to 15 places just by evaluating atan(1/28) to that many places. By comparison, Machin's original formula requires us to evaluate atan(1/5). For more on this type of formula, see Machin's Merit.

Return to MathPages Main Menu