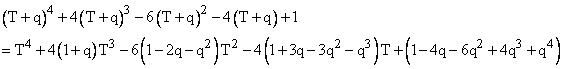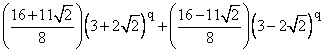Miscellaneous Diophantine Equations

x² + y² = z⁴,   x + y = w²

In a letter to St. Martin and Frenicle on May 31, 1643, Fermat asked for a rational right triangle whose hypotenuse and the sum of whose legs are squares. In other words, he suggested the problem of finding a Pythagorean triple x,y,z with x² + y² = z² such that x+y and z were both squares. He then gave the solution

and stated that it was the smallest possible.  Dickson describes several solution methods, including the one used by Fermat, and another method by Euler. We seek two integers x,y such that  x + y is a square and x² + y² is a fourth power.  Euler noted that if we set x = p² - q² and y = 2pq then x² + y² is equal to the square (p² + q²)², and we can make p² + q²  a square by setting p = r² - s² and q = 2rs, which gives x² + y² = (r² + s²)⁴.  This also gives

Dividing through the right hand polynomial by s⁴ and setting t = r/s, we seek a rational number t such that

is a rational square. (This is an elliptic curve.) Since the leading and trailing coefficients are squares, it’s easy to see that this polynomial differs from (t² – 2t + 1)²  by  4t²(2t - 3), so we have the rational solution t = 3/2. However, we want the edge lengths x and y of our triangle to be positive, which requires p greater than q, which implies t must be greater than 2.414 or less than 0.414. The value t = 3/2 gives a negative value of x, so even though it is a solution, it doesn’t satisfy the implicit positivity requirement of Fermat’s original question. We therefore seek other solutions, to see if we can find one that gives positive values of x and y. To do this, suppose we set t = T + q in the above polynomial, where q is an arbitrary rational number. This gives

As before, it would be simple to find a rational value of T that makes this expression a square, provided the leading and trailing coefficients are squares. Notice that the trailing coefficient has the same form as the original polynomial in t, which we already know how to make into a square, by setting q = 3/2, which was our previous solution. When we make this substitution, the polynomial becomes

This differs from the square of (T² - 37T - 1/4)²  by  T²(84T - 1343), and hence a solution is T = 1343/84. Therefore, we have t = T + q = 1469/84, so we can take r = 1469 and s = 84, and compute x = 4565486027761 and y = 1061652293520. This the solution Fermat sent to Frenicle, and we can confirm that

We could continue to generate larger solutions by iterating the steps that took us from the original solution 3/2 to the next solution 1469/84. Presumably Fermat’s assertion that this is the smallest solution was based on his understanding that all the solutions can be generated in a similar way. This is equivalent to the “tangent and chord” method in the theory of elliptic curves.

a⁴ + b³ = c²

There are infinitely many primitive solutions to the Diophantine equation

To prove this, factor the equation  b³ = c² - a⁴  as

If a and c have opposite parity the two factors on the right are co-prime, so we have integers m,n such that

It follows that we have a solution if we can find integers a,c of the form

These values of a² and c are clearly integers (since m and n are both odd), so the only constraint on m,n is that they make "a" an integer.  There are several ways of constructing an infinite family with this  property.  For example, if we restrict ourselves to "twin" values of m and n, meaning that m = k+1 and n = k-1, the above equation for a² becomes

which is a Pell equation.  By the usual methods we have the solutions given by k = 0, 1, 4, 15, 56, 209, 780, ... and in general by the recurrence

Obviously these values of k alternate between odd and even.  The odd values give even values of m and n, so those correspond to non-primitive solutions, such as 26⁴ + 224³ = 3420², whereas the even values of k give odd values of m and n, and the corresponding solutions of the original equation are primitive.  For example, with k = 4 we have m = 5, n = 3, which gives the solution a = 7, b = 15, c = 76.  The next primitive solution in this family is based on the Pell solution k = 56, which gives m = 57, n = 55 and so a = 97, b = 3135, c = 175784.  The next such solution would be based on the even Pell solution k = 780, and so on.  We can create other infinite families in a similar way by defining a linear relation between m and n.

Someone asked how to find the integer solutions of

This can be viewed as a Pell equation with an extra condition on the solution.  Squaring both sides twice gives

which implies that n(kn+1) is a square.  Since n and kn+1 have no common factor they must each be squares, so we know there exist integers x,y such that

Eliminating n from the first two equations gives the Pell equation

For any given k we're looking for solutions x,y such that x+y is a square.  Of course, for any positive integer k there are infinitely many solutions to the Pell equation, but solutions with x + y = square are rare.  For example, with k=8 the values of x+y such that x,y satisfy the Pell equation are

This gives the sequence 4, 23, 134, 781, 4552..., which satisfies the second order recurrence s[j] = 6s[j-1] - s[j-2].  The initial value 4 in this sequence corresponds to the solution n=1,k=8,m=2 of the original equation.  The question is whether this sequence contains any squares after the initial value 4. 

So the problem reduces to finding the square terms of a general second-order recurring sequence, like the Fibonacci sequence.  It is known (but not entirely trivial to prove) that the only square Fibonacci numbers are 0, 1, and 144.  Thus to fully characterize all the solutions of the original equation we would need to prove the analogous result for each of the general second-order recurrence sequences arising as solutions of the Pell equation with all values of k.

n! + 1 = x²

There are only three known solutions (in positive integers) of the equation n! + 1 = m², namely

Are there any others?  The latest result I've seen is a paper by Berend and Osgood in J Num Thry (1992, vol 42), which gives a proof that for any polynomial P of degree > 1 the set of positive integers n for which P(x) = n! has an integer solution x is of zero density.  However, the paper states that it is not known if the particular equation x² - 1 = n! has only finitely many solutions.  Does anyone know of any further results?

Return to MathPages Main Menu