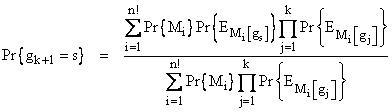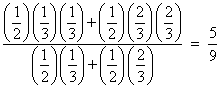Probabilities With Renaming

Suppose the outcome of each of a series of trials can be one of the events E_i (i=1 to n) with the respective probabilities Pr{E_i}. Prior to the first trial the events are renamed by applying the inverse of a particular permutation "M" to the indices. Thus, if event E_i is renamed E_j, then M[j] = i. Since there are n indices there are n! possible permutations, which we can denote by M_i (i = 1 to n!). Each of these has a known probability, denoted by Pr{M_i}.

Now suppose the first k trials yield the events with the permuted indices g₁, g₂,..., g_k. For example, if the outcome of the third trial is E₇ then g₃ = 7. (Here the “7” is the renamed index, so this is not necessarily the original E₇ whose probability is given.) Given the values of all Pr{E_i} for i = 1 to n (representing the unpermuted indices), and the probabilities Pr{M_i}, i = 1 to n!  of the possible permutations, and given the results g_i (i=1 to k) of the first k trials, what are the probabilities that g_k+1 = s for any given index s?

If we knew the indices were not permuted at all, we would immediately know the probabilities for each of the events, but since the indices are permuted, we must infer something about the probabilities of the permuted events from the k outcomes already observed.

The answer is the ratio of {the sum of the probabilities of all the possible sequences of events (including choice of permutation) with the given values of g_i, i = 1 to k+1} divided by {the sum of the probabilities of all possible sequences with the given values of g_i, i = 1 to k}. Symbolically this can be written in the form

For example, consider the case of n = 2 with Pr{E₁} = 1/3 and Pr{E₂} = 2/3. Let M₁ denote the identity permutation and M₂ the reversal, and suppose we are given that Pr{M₁} = Pr{M₂} = 1/2. Also we have k = 1 with g₁ = 1. The probability that g₂ equals 1 is

Now suppose Pr{A} = 1/3, Pr{B} = 2/3, and we are told that the events are being renamed, with a 50% chance that they will be kept that same, i.e., that p(A') = 1/3 and p(B') = 2/3, and a 50% chance that they will be switched, resulting in p(A') = 2/3 and p(B') = 1/3. After the die is rolled we are told that event A' occurred. What is the probability that on the next roll, A' occurs again? More generally, what if Pr{A} = p, Pr{B} = q = 1-p, Pr{A'=A} = r, and Pr{A'=B} = s = 1-r ?  The answer is that A' occurs again with probability

Thus if we have p = 1/3, q = 2/3, r = s = 1/2, the result is 5/9.

Return to MathPages Main Menu