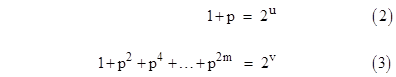|
Sum of Divisors Equals a Power of 2 |
|
|
|
In 1959 the Polish mathematician Waclaw Sierpinski noted that the sum of the divisors of an integer N>1 is a power of 2 if and only if N is a product of distinct Mersenne primes. (See "Sur les nombres dont la somme de diviseurs est une puissance du nombre 2" Calcutta Math. Soc. Golden Jubilee Commemoration 1958/59, Part I. Calcutta: Calcutta Math. Soc., pp. 7-9, 1963.) The Problems section of a 1990 issue of Mathematics Magazine challenged itís readers to prove this assertion. |
|
|
|
Let N > 1 be an integer with the prime factorization |
|
|
|
|
|
|
|
where the pj are distinct primes. Since the sum of divisors of N, denoted by σ(N), is multiplicative, we have |
|
|
|
|
|
|
|
from which it follows that σ(N) is a power of 2 if and only if each of σ(pjaj) is a power of 2. Now, for any prime power pa we have |
|
|
|
|
|
|
|
For this sum to be even, both p and a must be odd. Thus there is a non-negative integer m such that a = 2m + 1, so we can factor (1+p) out of equation (1) to give |
|
|
|
|
|
|
|
Clearly σ(pa) is a power of 2 if and only if all of its factors are powers of 2, so we have |
|
|
|
|
|
|
|
for integers u > 1 and v ≥ 0. Equation (2) proves that p must be a Mersenne prime, because it has the form p = 2u − 1, where u is obviously a prime because 2ab − 1 has the non-unit factor 2a − 1 for any integers a,b > 1. Thus a necessary condition for σ(N) to be a power of 2 is that N be the product of Mersenne primes. |
|
|
|
To prove that N is necessarily the product of distinct Mersenne primes, suppose that equation (3) were satisfied for some positive integer m (corresponding to an exponent aj > 1 in the prime factorization of N). Then v > 0, and m must be odd, so we have m = 2r+1 for some non-negative integer r. We could then factor (1 + p2) from the left side of (3) to give |
|
|
|
|
|
|
|
which implies that (1 + p2) is a power of 2. However, from equation (2) we also have |
|
|
|
|
|
|
|
proving that 1 + p2 has an odd factor greater than 1, contradicting the previous equation. It follows that the only solution of equation (3) (if p is a Mersenne prime) is the trivial solution with m = v = 0. Therefore, each non-zero exponent in the prime factorization of N must equal 1, so N must be a product of distinct Mersenne primes. |
|
|
|
Finally, we observe that the stated condition is also sufficient, since σ(p) = 1 + p is (by definition) a power of 2 if p is a Mersenne prime. |
|
|