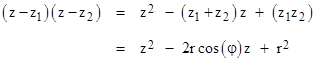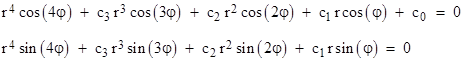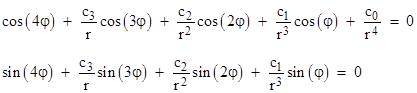The Fundamental Theorem of Algebra

There is a Russian emissary here whose two young and intellectually gifted daughters I was supposed to instruct in mathematics and astronomy. I was, however, too late, and a French émigré obtained the position.                 C. F. Gauss, 1798

Gauss’s doctoral dissertation, published in 1799, provided the first genuine proof of the fact that every polynomial (in one variable) with real coefficients can be factored into linear and/or quadratic factors. Imaginary and complex numbers were not widely accepted at that time, but today this proposition – traditionally called the fundamental theorem of algebra - is usually expressed by saying that every polynomial of degree n possesses n complex roots, counting multiplicities. Although Gauss’s 1799 proof focused on polynomials with real coefficients, it isn’t difficult to extend the result to polynomials with complex coefficients as well. By modern standards, Gauss’s proof was not rigorously complete, since he relied on the continuity of certain curves, but it was a major improvement over all previous attempts at a proof.

Only about a third of Gauss’s dissertation was actually taken up by the proof. The rest consisted of a rather frank assessment of the previously claimed proofs of this proposition by D’Alembert, Euler, Legendre, Lagrange, and others. Gauss explained that all their attempts were fallacious, and indeed that they didn’t even address the real problem. They all implicitly assumed the existence of the roots, and just sought to determine the form of those roots. Gauss pointed out that the real task was to prove the existence of the roots in the first place, and only then to establish their form. (He complained in a letter to his friend Bolyai about “the shallowness of contemporary mathematics”.) It’s clear that Gauss attached great importance to this theorem, since he returned to it repeatedly, publishing four proofs of it during his lifetime. The fourth of these was in the last paper he ever wrote, which appeared in 1849, exactly 50 years after his dissertation on the same subject.

The phrase “fundamental theorem of algebra” may be considered somewhat inaccurate, because the proposition is actually part of complex analysis. (It might even be regarded as an example of Gödel’s incompleteness theorem, i.e., a meaningful and true proposition that cannot be proven within the context in which it is formulated.) A huge number of proofs have been devised, making use of a wide range of mathematical concepts. In general a polynomial of degree n is defined as a function of the form

where z is a complex variable and c₀, c₁, …, c_n–1 are complex constants.  Of course, it suffices to prove that every polynomial has at least one complex root, because by ordinary algebraic division we can divide by the corresponding linear factor to give another polynomial whose degree is reduced by 1. Repeating this process, we get all n of the roots.

For the case of real-valued coefficients and odd degree n, it’s easy to see that a real root exists, because in that case the value of f(z) is positive for sufficiently large positive values of z, and negative for sufficiently large negative values of z, and since the function is continuous, it must pass through zero at some point in between. (We accept the intuitive aspects of continuous curves without rigorous proof.) If the degree n is even, the function may still cross zero, and each such crossing corresponds to a real root. Hence the only non-trivial task is to prove that a real polynomial of even degree, and that does not cross zero (for real arguments), is divisible by a quadratic factor, i.e., a polynomial of the form z² + a₁z + a₀ for some real values of a₀ and a₁. Hence the first case in doubt is the quartic, i.e., a polynomial of degree n = 4, which can be written as

We will focus on just the case n = 4, but the arguments are completely general, and apply to any higher degree. Assume this function does not equal zero for real values of z (because if it does, we can divide by the corresponding linear factors to arrive at a polynomial of lower degree). As mentioned above, Gauss’s 1799 proof dealt only with polynomials with real coefficients, and avoided any explicit use of complex numbers, but his proof is clearly based on the behavior of complex numbers. Instead of claiming that this polynomial is divisible by each of the linear factors (z–z₁) and (z–z₂) where z₁ and z₂ are complex conjugate roots

he simply asserts that f(z) is divisible by the product of these two factors, i.e., by the quadratic with real coefficients

To prove this, he essentially inserts one of the individual roots into f(z) = 0, and then splits the result into two equations, one consisting of just the real terms and the other consisting of the imaginary terms. Of course, he doesn’t proceed explicitly in this way, but clearly substitution of the exponential form of either z₁ or z₂ into f(z) = 0 leads to the two equations

Gauss stated that these equations are “usually given with the aid of imaginaries (cf. Euler), but I found it worthwhile to show that it can be demonstrated in the same easy way without their aid”. Each of these equations described a locus of points on the (r,φ) plane. The necessary and sufficient condition for f(z) to be divisible by the specified quadratic factor is that there be some point of intersection between these two loci.

To prove the existence of such an intersection, Gauss first observes that we can regard the left hand sides of those equations (with arbitrary r and φ) as altitudes above the (r,φ) plane, so they each define a continuous surface. For sufficiently large r (which he takes to always be positive, since negative values of z are given by a suitable angle φ), the leading terms are larger than the sum of all the other terms, and so the surface clearly lies above the plane in some locations and below the plane in others. Since it is a continuous surface, it must pass through the plane, and the intersection of the surface with the plane gives the two loci represented by the two equations above. He then divides through the equations by r⁴ and writes them in the form

Hence (he says), at an infinite distance from the origin (i.e., as r increases to infinity), these curves coincide with (or rather, are asymptotic to) the loci represented by

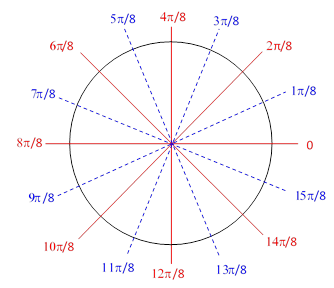
where n = 4 for our example. The solutions of these equations are φ = (π/2n)(2k+1) and φ = (π/2n)(2k) respectively. These solutions are independent of r, so they represent radial lines on the (r,φ) plane. Therefore, the original two loci are asymptotic to the radial lines shown below.

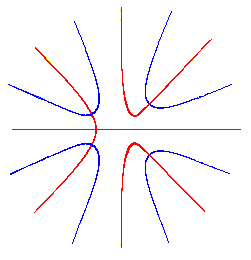
As a concession to “readers less familiar with general and abstract investigations”, Gauss included a plot of the curves for a specific example, namely the quartic polynomial

These curves are shown in the figure below.

The four complex roots corresponds to the four points of intersection between the red and blue curves. (The roots come in conjugate pairs, as can be seen from the symmetry about the horizontal axis.) Gauss then explains why, in general, we are guaranteed an intersection. He argues that each branch must be continuous, and therefore the curve on each branch must pass from one asymptote to another. Furthermore, the asymptotes occur alternately, so no matter how they are paired, they must cross at some point. He showed this by pointing out that, if we are to avoid any crossings, then any two connected red asymptotes must completely enclose an even number of blue asymptotes (so they can be connected in pairs without crossing the red connection), and likewise any two connected blue asymptotes must enclose an even number of red asymptotes, and so on. But eventually we must arrive at a single enclosed asymptote, so it must intersect the enclosing curve. This completes the proof.

For a streamlined version of Gauss’s proof, making free use of complex numbers (but taking the properties of continuity for granted), consider again the general polynomial of degree n with complex coefficients

and again put z = re^iφ, so we have

For sufficiently large r the first terms is larger than all the others combined, so if we move the point z around a circle of radius r (on the complex plane) centered on the origin, the corresponding points f(z) trace out a closed curve that loops around the origin n times. A rough illustration of this is shown in the left-hand figure below.

Now, as r goes zero, the value of f(z) goes to c₀, and when r is exactly zero, the locus of z values is just a single point at the origin, and the corresponding locus of f(z) values is the single point at c₀.  Assuming c₀ is not equal to zero, these are two different points. It follows that as r is varied continuously from large values (as in the left-hand figure) to small values (as in the right-hand figure), the blue locus of f(z) values must be dragged across the origin. In fact, all n of the loops must cross the origin, and the z values for which this occurs are the n complex roots of the polynomial. This completes the proof.

Another well-known proof is based on the properties of analytic function. Recall that a function F(z) is analytic in some region if it can be expressed as a convergent power series

in that region. As an example, the function F(z) = 1/(1–z) is analytic because it is equal to the convergent series

However, this series is convergent only for |z| less than 1, which is the root of the denominator. For z = 1 the denominator goes to zero, and the function goes to infinity. In general, the series expansion of a polynomial about some point converges only within the largest circle centered on that point that does not enclose any “poles”. In other words, the disk of convergence for the power series of a rational function extends only to the nearest pole. Now, suppose we have a (non-constant) polynomial f(z) that has no complex root. It follows that the function F(z) = 1/f(z) has no poles, so it is analytic everywhere, and hence the power series for F(z) converges for all z. But this is impossible, because the magnitude of f(z) becomes arbitrarily large as z increases to infinity, and hence the magnitude of F(z) = 1/f(z) becomes arbitrarily small, and yet the magnitude of the power series for F(z) becomes arbitrarily large. The only exception would be if all the coefficients a_j of the power series were zero except for a₀, but in that case F(z) is a constant, whereas we stipulated that f(z) and therefore 1/f(z) is not constant. (The fact that a bounded function which is regular at every point must be a constant is called Liouville’s theorem.)

Return to MathPages Main Menu