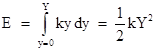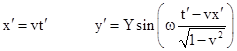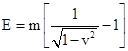A Mass and Spring System in Motion

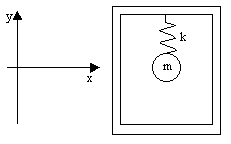
Suppose a mass m is attached to a spring, which in turn is attached to a very massive framework floating far out in space (no gravitational field), as shown below.

The mass is allowed to oscillate freely in the y direction. The force of the spring is zero when the mass is at y=0, and at other positions the force is given by F = −ky, where k is the spring constant. The spring is perfectly conservative, so the change in energy stored in the spring is dE = Fdy = −ky dy. Hence the absolute value of the energy stored in the spring at the point y = ±Y of maximum deflection is

The equation of motion for this simple system is

and the general solution is a harmonic oscillation

Now consider another inertial coordinate system x′,y′,t′ whose spatial origin is moving in the x direction with speed v relative to the x,y,t system, so we have

In terms of the primed coordinates the motion of the mass is

Substituting for x′ into the expression for y′ gives

As expected, this implies that the mass and spring oscillations occur more slowly with respect to the relatively-moving primed coordinates. On the other hand, the equation of motion (in the y′ direction) with respect to these coordinates has the same form as it does with respect to the original coordinates, i.e., we have

for constants m′ and k′. Consequently we must have

It follows that

To verify this, we first note that the familiar relation between rest mass m and relativistic mass m′ gives

To determine the value of the ratio k′/k, note that the speed of the mass in the y′ direction is

The maximum speed occurs at the null point of the spring, where the cosine factor is unity, so the kinetic energy of the mass in the y′ direction is

up to the second order in v. At the conditions of maximum deflection (i.e., when y = ±Y), this energy must be contained entirely in the form of potential energy of the spring, which as we saw previously is given by

Since the amplitude Y of the oscillation is unchanged (because y = y′), the ratio of the potential energies at the conditions of maximum deflection must equal the ratio of spring constants. With respect to the original system, the total energy was (1/2)mYω², so the ratio of the spring constants is

Combining this with the ratio m/m′, we see that indeed the natural frequency of oscillation for the mass and spring system moving transversely at the speed v is consistent with the relativistic mass m' and the relativistic spring constant k' of the moving system.

It's interesting that, with respect to the relatively moving coordinates, the mass of the oscillating object is increased, but the system energy, which oscillates between kinetic and potential, is decreased. This is because, even though the oscillating mass is greater, it's speed is lower, and speed occurs as a squared term in the expression for kinetic energy, whereas mass occurs only to the first power.

Incidentally, in the above derivation we expressed the kinetic energy only up to the second order in v. To be exact, we should have used the expression

However, the final result would be the same, provided we use the full relativistic expressions consistently for all variables.

Return to MathPages Main Menu