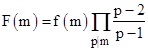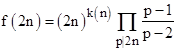|
Evidence for Goldbach |
|
|
|
Goldbach's famous conjecture is that every natural number can be expressed as a sum of three primes, which, as Euler pointed out, is equivalent to the statement that every even number can be expressed as a sum of two odd primes. There has been a great deal of work on this question, and many strong results have been proven, but we still don't have a complete proof of the conjecture. |
|
|
|
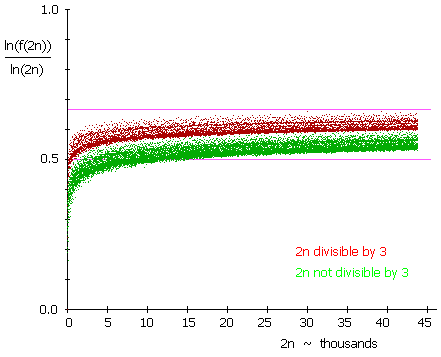
Of course, even though we are unable to prove that every even number is expressible in at least one way as a sum of two odd primes, the empirical evidence is that most even numbers are expressible in many ways as a sum of two odd primes. In fact, if we let f(n) denote the number of distinct ways in which n can be expressed as a sum of primes, then empirically it appears that f(2n) is greater than the square root of 2n for all 2n greater than 15788. Also, an upper bound on f(2n) seems to be given by (2n)2/3, although perhaps the exponent should be a bit greater. |
|
|
|
Assuming a relation of the form f(2n) = (2n)k, the value of the exponent k is given by k = ln(f(2n))/ln(2n), so we can plot this ratio to see how it behaves. A plot of these exponents for 2n up to 45000 is shown below. |
|
|
|
|
|
|
|
This shows that there are two distinct populations, depending on whether or not n is a multiple of 3. The reason for this is simply that if 2n = 0 (mod 3) then two primes p,q (greater than 3) such that p + q = 2n can be either p=1,q=2 or p=2,q=1 (mod 3), whereas if 2n = 1 (mod 3) we must have p = q = 2 (mod 3), and if 2n = 2 (mod 3) we must have p = q = 1 (mod 3). Hence there are twice as many "chances" for finding suitable pairs of primes when 2n is a multiple of 3 than when it isn't. If we divide each f(2n) by 2 whenever 2n is a multiple of 3, the upper band in the above figure drops down to coincide with the lower band, cutting the width of the combined band in half. (Notice that cutting f(2n) in half before computing log(f(2n))/log(n) is equivalent to subtracting log(2)/log(n) from the ratio.) |
|
|
|
Similarly if 2n = 0 (mod 5) we have four possibilities |
|
|
|
|
|
|
|
whereas if 2n = 1 (mod 5) we have only three possibilities |
|
|
|
|
|
|
|
The other residue classes also give three possibilities each, so we find that there are 4/3 as many chances for finding suitable pairs of primes when 2n is a multiple of 5 than when it isn't. So, to place them all on a common footing, we can multiply each f(2n) by 3/4 if 2n is a multiple of 5. |
|
|
|
Likewise for every odd prime p we can apply a factor of (p−2)/(p−1) to the function f(2n) if 2n is divisible by p. This effectively normalizes the function, and we arrive at the function |
|
|
|
|
|
|
|
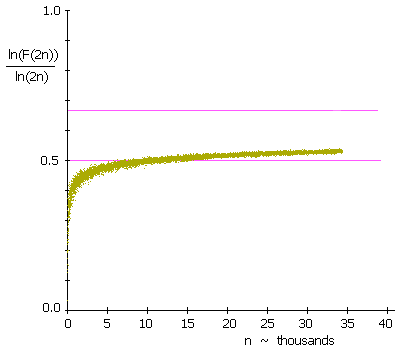
In other words, F(m) is defined as f(m) multiplied by a factor of (p−2)/(p−1) for each prime p that divides m. If we plot the log of this function divided by the log of n we find that the scatter is reduced almost entirely to a single line as shown below: |
|
|
|
|
|
|
|
Thus, although we lack a rigorous proof, this numerical evidence lets us feel confident not only that f(2n) is never equal to 0 (which would correspond to a point at negative infinity on the above plot), but that we can closely estimate of the value of f(2n) by |
|
|
|
|
|
|
|
where k(n) is the value from the plot above. As mentioned above, we clearly have k(n) > 1/2 for all n greater than 15788. We could further refine this approach, by accounting for higher-order divisibilities, and collapse the curve even more, until it approaches a single-valued curve. |
|
|