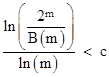Differences Between Powers

Now my charms are all o’erthrown

And what strength I have’s mine own,

Which is most faint.

Catalan conjectured that the equation

has no integer solutions with m,n > 1 other than 3² – 2³ = 1.  In 1976 Tijdeman proved that this conjecture is true except for possibly a finite number of exceptions. The proof is not simple, and the finite number of possible exceptions is huge – beyond any practical ability to actually evaluate. Nevertheless, despite the difficulty of proving Catalan’s conjecture completely, many special cases of the conjecture can be proven by very simple arguments.

For example, it's easy to show that there do not exist powers 2^m and 3ⁿ that differ by 1 other than the four cases (2,1), (2,3), (4,3), and (8,9). Consider the case 3ⁿ – 1 = 2^m.  If n is composite of the form n = ab, then (3^a – 1) and (3^b – 1) must both be powers of 2. It follows that for each prime p that divides n we must have (3^p – 1) = 2^u for some integer u. However, no odd prime power of 3 is congruent to 1 (mod 8), so we can rule out any odd prime divisors of n (for u > 2). This leaves only the case

for which the only two solutions are {k = 0, m = 1} and {k = 1, m = 3}. There can be no solution for k>1 because in that case the expression on the left hand side is divisible by  (3² + 1) = 2(5), and thus is not a pure power of 2.

Likewise we can show that there are no positive integral solutions to  2^m – 3ⁿ = 1  other than  m = 2, n = 1. Written in the form  2^m – 1 = 3ⁿ  it's obvious that if m is composite of the form ab then (2^a – 1) and (2^b – 1) must both be powers of 3. It follows that for each prime p that divides m we must have 2^p – 1 = 3^u for some integer u.  However, no odd power of 2 is congruent to 1 (mod 3), so we can rule out any odd prime divisor of m. This leaves only the case

for which the only two solutions are {k = 0, n = 0} and {k = 1, n = 1}. There can be no solution for k>1 because in that case the left hand side is divisible by 2⁴ – 1 = (3)(5), and thus is not a pure power of 3.

Returning to the general equation, it’s obvious that any solution of (1) must have (a,b) = 1, which is to say that “a” and “b” must be co-prime, because any common factor must also divide 1. Also, one of “a” and “b” must be odd and the other must be even. Now, we can re-write (1) in the form

and observe that, for any prime p dividing m, the quantity a^p – 1 must be a pure power of b. This leads us to examine the values of p such that a^p is congruent to 1 modulo b, or modulo higher powers of b. We always have a⁰ = 1 (mod b), and the values of a^k (mod b) are periodic with a period τ dividing ϕ(b) where ϕ is the totient function. Therefore, every prime divisor of m must equal τ, which requires that τ itself must be a prime. Thus the order of “a” modulo b^k must have the same value for k = 1, 2, .., n, and this value must be prime. This is sufficient to immediately rule out cases such as a = 2, b = 5, with n > 0, because the order of 2 modulo 5 is 4, which is not a prime.

On the other hand, if the order of “a” satisfies the stated condition, then m is a pure power of τ, and hence any solution of (2) must be of the form

As an example, the order of 2 modulo 7 equals the prime 3 (because the powers of 2 modulo 7 are 1, 2, 4, 1, 2, 4, …), whereas the order of 2 modulo 7² equals the composite 21. Therefore the only possible solutions of (2) with a = 2 and b = 7 must have n = 1, and must be of the form

This does indeed have the solution k = 1, but for any greater value of k the left hand side is divisible by 2⁹ – 1 = (7)(73), and hence does not equal 7.

For another example, consider the case a = 19, b = 42. In this case the order of “a” is 6 modulo b, b², and b³, as shown by the factorization

However, since this quantity is also divisible by 5 and 127, it follows that 19^m – 42ⁿ cannot equal 1 for any natural numbers m and n. In this way it’s typically trivial to prove that equation (1) has no solutions for given values of “a” and “b”, simply by examining the factorization of a^τ – 1 where τ is the order of a modulo b and b². The difficulty of Catalan’s general conjecture is in proving that, for all values of “a” and “b”, the quantity a^τ – 1 must always be divisible by some prime not contained in b.

As an aside, we will mention a slight variation on the above arguments. Observe that (for example) if 3^s = (2^r + 1) then clearly 3^s is less than 2^(r+1), so we have s < (r+1) ln(2)/ln(3). Also, by simple congruence arguments, if 3^s – 1 is divisible by 2^r, then s is divisible by 2^(r–2). (This just extends the fact used above that if 3^s – 1 is divisible by 8, then s must be even.) Therefore we have 2^(r–2)  ≤  s  <  (0.6309)(r+1). For r = 3 this requires 2 ≤ s < 2.52, so s = 2 is a possibility (fortunately), but for any r > 3 the value of 2(r–2) exceeds 0.6309(r+1), so no other solutions are possible.

It’s also interesting to consider whether the difference between two powers can equal some other small integers. In other words, we seek solutions of

for a given integer value of c. This is called Pillai’s equation. For example, having proven that 2^m – 3ⁿ can never equal 1, except in the trivial cases (m=1,n=0) and (m=2,n=1), we can ask whether that difference can equal other small values. By simple divisibility we can rule out 2, 3, 4, 6, etc., but we can’t rule out 5, 7, 11, etc.  To examine the minimum values taken on by 2^m – 3ⁿ for integer arguments m and n, we first note that this function equals zero precisely when

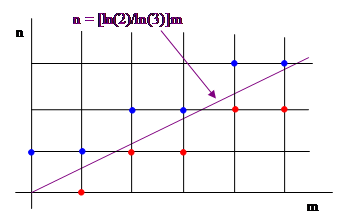
The ratio ln(2)/ln(3) is irrational, so this equality is never satisfied for integers m,n, but we can consider the pairs of integers that come closest to satisfying this equality, as depicted in the figure below.

For each integer m let A(m) and B(m) denote the nearest lattice points above and below the line respectively. Using the ceiling and floor symbols, these functions can be expressed as

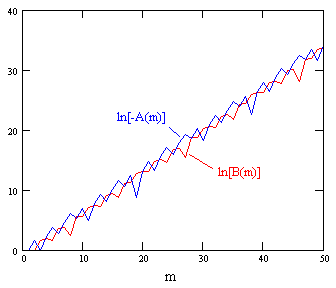
Clearly A(m) will be negative and B(m) will be positive. A plot of the logarithms of (the magnitudes of) these functions is shown below.

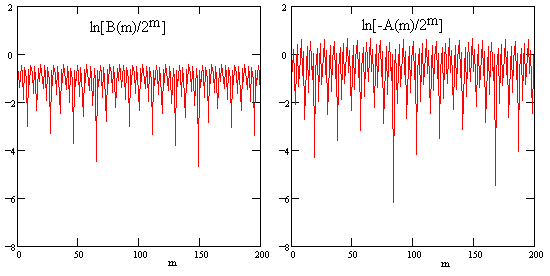
Plotting the logarithms of –A(m)/2^m and B(m)/2^m for m up to 200, we get the results shown below.

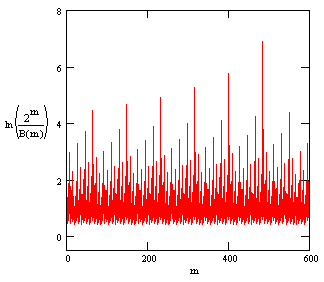
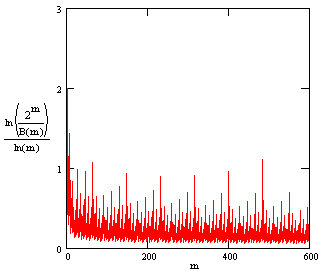
Each downward spike is at a value of m for which a locally minimal value of B(m) of A(m) occurs. To assess whether the spikes tend to become more severe, we can plot the logarithm of 2^m/B(m) for values of m up to 600, as shown below.

There does appear to be a long-term tendency for the sequence of spikes to increase. (In the hierarchy of sub-sequences, each sequence of spikes appears to increase.) This gives a very slow secular increase. We might speculate that if we divide this function by ln(m), the resulting function would be bounded by some fixed upper value. Thus function is shown in the figure below.

It is at least plausible that this function never exceeds some constant c, which implies the inequality

which can also be written in the form

A similar argument leads to a conjecture of the same form for the magnitude of the function A(m). Indeed, Tijdeman proved that there exists a number c ≥ 1 such that

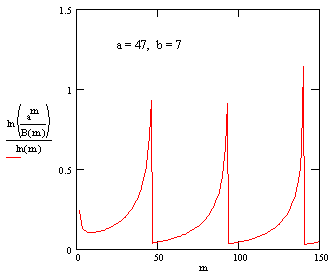
The same behavior is apparent for arbitrary values of “a” and “b”, which is to say, the minimum different between powers of two co-prime numbers seems to increase almost exponentially. In cases where the ratio ln(a)/ln(b) is close to a small rational number, the minimum difference function takes on the appearance of a piecewise continuous function. For example, with a = 47 and b = 7 the normalized minimum difference function is as shown below.

The period of this pseudo-function is 47, related to the fact that

and also to the fact that 2(47) = 93+1.

Return to MathPages Main Menu