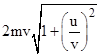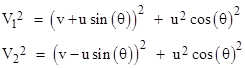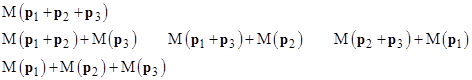The Quantity of Motion

During the late 17th and early 18th centuries, as the science of dynamics was being established, there were competing ideas as to the best (or “correct”) way of quantifying motion. In ancient times – and even in some contexts today – the word “motion” was taken to signify a purely kinematic attribute of a physical entity, quantified by the parameter v, representing the distance traveled per unit time. Of course, the concepts distance and time are non-trivial in themselves, leading to conundrums such as those discussed by Zeno, but nevertheless the kinematic concept of motion seemed satisfactory and unproblematic to most people in ancient times. However, the modern science of dynamics was based on a profoundly different idea as to how to quantify “motion”. At the beginning of the Principia, after defining “quantity of matter” as the product of density and volume, Newton proposed the following definition:

The quantity of motion is the measure of the same, arise from the velocity and quantity of matter conjointly.

In other words, rather than defining the quantity of motion of a given object as simply the kinematic velocity v of the object, he defined it as the product mv, where m is the mass of the object. This is an immensely significant change in the concept of motion, shifting it from a kinematical to a dynamical basis. It implies that “motion” without mass (or, as we would now say, mass-energy) is impossible, i.e., that the purely kinematic concept of motion is meaningless, and that mass represents a scale factor on the spatio-temporal parameter v.

Since the quantity (singular) of motion is a scalar, Newton’s definition implicitly treated the parameter v as what we would call the scalar speed, rather than the vector velocity. Hence the quantity of motion is not precisely identical to the modern concept of momentum, which is a vector. Based on the scalar quantification of “motion”, Newton had to acknowledge that, contrary to the teachings of Descartes, the “quantity of motion” is not conserved. In Question 31 at the conclusion of The Opticks he wrote

From the various composition of two motions, ‘tis very certain that there is not always the same quantity of motion in the world. For if two globes joined by a slender rod revolve about their common center of gravity with a uniform motion, while that center moves on in a right line drawn in the plane of their circular motion, the sum of the motion of the two globes, as often as the globes are in the right line described by their common center of gravity, will be bigger than the sum of their motions when they are in a line perpendicular to that right line. By this instance it appears that motion may be got or lost.

This is an interesting illustration, showing that Newton really did (in this context) conceive of the “quantity of motion” as a scalar rather than a vector. The two conditions he considered are shown in the figure below.

In the left hand configuration the quantities of motion of the two individual globes are m(v+u) and m(v-u), giving a total quantity of 2mv, whereas in the right hand configuration each globe has a squared speed of v² + u², so the total quantity of motion is

Newton doesn’t comment on the fact that the total quantity of motion in any particular direction is constant, nor does he mention that the sum of the expressions mv² for the two globes is constant. This latter invariance applies not only to the two configurations, parallel and perpendicular to the overall direction of motion, but to all configurations, as shown by the fact that the squared speeds of the globes when the connecting rod makes an angle θ with the direction of motion of the center of gravity are

Hence the sum is always 2(v² + u²). It’s tempting to imagine that this is how Leibniz arrived at the idea of vis viva, rather than momentum, as the fundamental conserved quantity. However, his actual reasoning was evidently based on consideration of free-fall. In 1686 he wrote

I suppose the same force is requisite to raise a body A of one pound weight, to the height of four yards ; which will raise the body B, of four pounds weight, to the height of one yard. This is granted both by the Cartesians, and other philosophers and mathematicians of our times. And from hence it follows, that the body A, by falling from the height of four yards, acquires exactly the same force, as the body B by falling from the height of one yard.

Of course, Leibniz was not using the word “force” here in the way that Newton was to define the word in Principia, published a year later. Leibniz used the word “force” to signify what we would call “work”, as the thing acquired by a body when in motion, a thing to which he granted ontological status (unlike space and time). There is a certain plausibility to his argument, because the effort required to raise an object by one yard (near the Earth’s surface) is sensibly independent of the height, so raising one object by four yards or four identical objects by one yard ought to require the same effort. Naturally we can simply define this to be the meaning of the words (effort, work, or force), but Leibniz’s point was that this “effort” is the most ontologically significant quantity associated with motion. The followers of Descartes, and later the followers of Newton, also quantified motion in terms of free-fall, but instead of regarding as fundamental the weight of an object multiplied by the spatial extent of the fall (from rest), they focused on the weight multiplied by the temporal duration of the fall. Galileo had shown that if an object, initially at rest, falls for a time Dt, it will fall a distance of Δs = g(Δt)²/2. It follows that the speed v of the object at the end of the fall can be inferred from either the distance fallen or the duration of the fall by the relations

Multiplying through each of these expressions by the mass m of the object, and noting that the downward Newtonian force (i.e., the weight) on the object is F = mg, we have

Thus the argument about whether momentum or kinetic energy (half of Leibniz’s vis viva) is more fundamental amounted to an argument about whether the temporal or the spatial interval is more fundamental. We now recognize that the three components of the momentum vector and the single scalar value of energy jointly comprise the energy-momentum 4-vector, whose absolute magnitude is the rest mass, in accord with the fundamental relativistic relation

where we have chosen units of space and time so that c = 1. This relation follows directly by multiplying through the Minkowski metric

by (m/dt)², and identifying the components

In view of this, the debate over vis viva and vis mortua (living force and dead force) does not seem to have been a pointless quibble over semantics and fuzzy definitions (as some have characterized it), but rather an examination of the components of the mass-energy vector and their relations to each other.

The collision of inelastic bodies was often used as a counter-example to Leibniz’s claim that vis viva is always conserved. Two identical lumps of clay, thrown together with equal and opposite speeds, will come to a halt, and seemingly their kinetic energy has vanished. However, Leibniz argued that the original kinetic energy remains, but has merely been re-distributed to imperceptibly small chaotic motions of the constituent parts of the bodies – a kind of motion that we call heat. This is indeed the case, and Leibniz ought to be credited for anticipating this important aspect of the conservation of energy (i.e., the convertibility between mechanical energy and heat), as well as an understanding of the mechanical basis of heat in terms of molecular motion. (Interestingly, during the spirited 19th century debate between the supporters of Joule and the supporters of Mayer as the “true” first discoverer of the convertibility between mechanical energy and heat, it appears that none of the participants thought of Leibniz.)

Returning to Newton’s discussion in The Opticks about how “motion may be got or lost”, it’s interesting that his example of the revolving globes fails to account for the vector nature of momentum. This is strange, because Newton obviously recognized the vectorial nature of momentum. Indeed, it could be said that his greatest achievement was the explanation of circular orbits in terms of a continuously-changing momentum (due to the change in direction) even while the “quantity of motion” remains constant. Hence, we would expect Newton to realize that, for the two revolving globes, the magnitude of the combined momentum is not equal to the sum of the magnitudes of the momenta of the individual globes, because momentum is a directed quantity. Likewise, if two identical bodies of mass m approach each other from opposite directions, each moving with speed v relative to their center of gravity, the sum of the magnitudes of their individual momenta is 2mv, whereas the momentum of the two bodies together is zero. (After the bodies collide, their combined momentum remains zero, but the momenta of the two individual bodies after collision depends on the elasticities of the bodies.)

It goes without saying the Newton was well-aware of all this, so we can only conclude that he carried along two related concepts of momentum, one a vector and the other a scalar, defined as the absolute value (magnitude) of the vector. Letting M(x) denote the magnitude of the vector x, we know that M(x + y) is not generally equal to M(x) + M(y). We may say that, in effect, there is constructive and destructive interference between the individual components. For a system consisting of three elementary particles with momenta p₁, p₂, p₃ we can define three distinct momentum scalars, one for each possible partition of the particles

The first of these represents the net quantity of motion of the aggregate, whereas the last represents the total quantity of motion, essentially summing the magnitudes of the momenta of the individual elementary constituents. In the limit of a continuous medium, the total quantity of motion would be the integral of the density times the speed, i.e.,

In the kinetic theory of gases, the mean value of the kinetic energy of the molecules corresponds to the heat content, and for monatomic gases this is proportional to the temperature. For a continuous medium the kinetic energy would correspond to

In addition to the kinetic energy, a continuous medium may also possess other energy modes, such as the potential energy of compression or tension, and the potential energy stored in “fields”. In a sense, the conservation of energy serves as an organizing principle, and in every situation we identify modes of energy so as to ensure that the total energy is conserved. It’s interesting to consider why the total quantity of motion does not afford an equally useful basis for organizing our knowledge. In Newton’s example of the revolving globes, the invariance of the sum of the squared speeds, even when the entire revolving configuration is set in uniform motion, is closely related to the relativity of motion in three-dimensional Euclidean space. Viewing the configuration in terms of a uniformly moving system of coordinates must not result in cyclic variations of the energy. The sum of squared speeds satisfies this requirement, but the sum of absolute speeds does not.

On the other hand, in the case of a harmonic oscillator, consisting of two masses connected by a spring, the total kinetic energy does vary cyclically, and yet we maintain conservation of energy by including the potential energy contained in the spring. Would it be possible to define such a thing as “potential momentum”, analogous to potential energy, for the case of the revolving globes? The rod holding the globes together is in tension, resisting the inertial tendency of the globes to fly apart, but this tension is constant, so it seems we cannot attribute any varying “potential momentum” to the rod. However, the tension in the rod is alternately parallel and perpendicular to the aggregate direction of motion, so if we were determined to conserve absolute momentum, we might define the potential momentum of tension as a function of the orientation of that tension relative to the direction of motion. We could assert that the potential momentum of a given amount of stress in motion is greater when the stress is perpendicular to the direction of motion than when it is parallel to the direction of motion. The spatial extent of the rod behaves in just this way when special relativity is taken into account, so at least some of the variation in “potential momentum” could be associated with the variation in length. But this doesn’t seem to lead to any natural concept of potential momentum that would keep the total absolute momentum constant.

In the context of special relativity, Newton’s example of revolving globes superimposed with translational motion has interesting implications. With respect to the rest frame of the center gravity, every orientation of the rod and globes is symmetrical, and the globes have constant speed, and the tension in the rod is constant. However, with respect to a relatively moving system of inertial coordinates, the speeds and kinetic energies of the individual globes are constantly changing, as are their resistances to acceleration. The total energy is constant, but some portion of that energy shifts back and forth between the two globes. At each instant, exactly equal amounts of energy are deducted from one globe and added to the other, and yet we know that energy cannot be conveyed instantaneously from place to place. The rod connecting the globes must be the means by which the energy is transferred, but is cannot be regarded as perfectly rigid. It’s spatial extend is varying in terms of the translating coordinates (so the globes describe elliptical rather than circular paths), and the phase relations between all the variations are such that the energy seems to be conveyed from one globe to the other instantaneously. It’s interesting that the rod is not conveying any net energy with respect to one frame of reference, but it is conveying net energy with respect to another.

It’s interesting that Newton seemed to consistently neglected interference phenomena, not only with regard to light, but also in the area of dynamics. As noted above, when dealing with an observable quantity M associated with a system variable x, we may find that M(x+y) does not equal M(x) + M(y). Two ways in which this inequality can occur are (1) non-linearity, and (2) interference. Leibniz’s vis viva, mv², is an example of non-linearity, since m(v₁+v₂)² does not equal mv₁² + mv₂². On the other hand, the Cartesian and Newtonian vis mortua, m|v|, is an example of interference, since m|v₁ + v₂| does not equal m|v₁| + m|v₂|.

Around 1800 Thomas Young went beyond Newton’s corpuscular concept of light, devising the “two slit” experiment to illustrate the wave-like interference characteristics of light. In terms of modern quantum electrodynamics, the probability amplitude for exchange of a photon along a given path is a complex number, having a phase as well as a magnitude (just as momentum is a vector, having a direction as well as a magnitude). As a result, even though the intensity at a certain location on the screen is positive when either one of the slits is open, the intensity at that location may be zero when both slits are open, because the contributions from the two slits may be out of phase. This is analogous to the fact that two bodies may each have a positive “quantity of motion”, but their combined “quantity of motion” may be zero.

Return to MathPages Main Menu