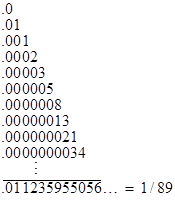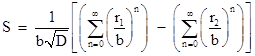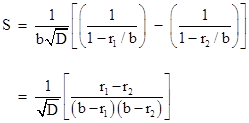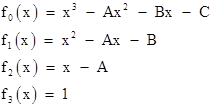Fibonacci, 1/89, And All That

One of the most frequently re-discovered facts about the Fibonacci numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... is that if we tabulate these numbers in a column, shifting the decimal point one place to the right for each successive number, the sum equals 1/89, as indicated below:

This is fairly trivial to prove, but it's an instance of an interesting general pattern involving geometrically weighted sums of the terms of arbitrary linear recurring sequences. In the simple case of Fibonacci numbers, or, a bit more generally, any monic second-order recurrence relation

the characteristic polynomial is

with the two (assumed distinct) roots

It follows that, for the initial values s₀ = 0, s₁ = 1, the nth term of the recurring sequence is

where D is the discriminant A² – 4B. The tabular summation described above, generalized to the base b, then consists of the terms

Substituting the previous expression for s_n and collecting terms, we have

If the geometric sums converge, (meaning that the roots with the largest magnitude is smaller than the base B), then we can write the sums in closed form

Since r₁ – r₂ equals √D, and noting that the denominator in the parentheses is f(b), because it is the product of terms of the form b minus each root of f, we have

Now, as noted above, the characteristic polynomial for the Fibonacci numbers is f(x) = x² – x – 1, so the sum S for the base 10 is given by setting b = 10, which gives S = 1/f(10) = 1/89.

It can be shown that this same summation applies to any (convergent) linear recurring sequence with the initial values 0, 0, ..,0, 1 (assuming the characteristic polynomial has distinct roots). For example, the sequence that satisfies the 3rd order relation

consists of the values 0, 0, 1, 3, 4, 4, 13, 47, ..., and the characteristic polynomial is

As can easily be verified, the sum of the terms of this sequence, written in base 10, arranged in a column with the decimal point shifted one place to the right for each successive number (as illustrated above for the Fibonacci numbers) is

This places the familiar "1/89" aspect of the Fibonacci numbers in perspective, and shows that it's just one special case of much more general result. It can be seen as a generalization of the simple geometric sum, because if we define the 1st-order recurring sequence by s₀ = 1 and s_k = As_k–1 then we have s_n = Aⁿ, and the characteristic polynomial is f(x) = x – A. So, the general formula reduces to the familiar sum

So far we’ve considered only recurrences with the initial values 0, 0, .., 0, 1, but we can also generalize to any set of initial values s₀, s₁, .., s_N–1 for an Nth-order recurrence. Let's write the general characteristic polynomial as

and then, calling this f₀(x), let's define the sequence of polynomials f_j(x) for j = 1, 2, ... as follows

For example, if f(x) = x³ – Ax² – Bx – C then we have

In these terms we can write the sum of s_n/bⁿ for n = 0 to infinity for any arbitrary linear recurrence (with distinct characteristic roots) and any initial values s₀, s₁,.., s_N–1 as

Of course, in our previous considerations we had s₀, s₁, .., s_N–2 all equal to zero, and s_N–1 equal to 1, so this reduced to b/f(b). In general we see that the sum equals a linear function of the N initial values, where the kth initial value has a coefficient of b f_k+1(b)/f₀(b). In the special case of sequences that satisfy the Fibonacci recurrence s_n = s_n–1 + s_n–2 beginning with the arbitrary initial values s₀ and s₁, the sum is given by [(b–1)s₀ + s₁] / 89.

Return to MathPages Main Menu