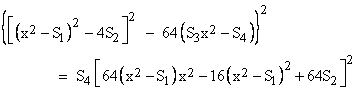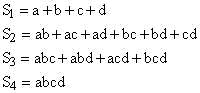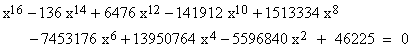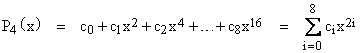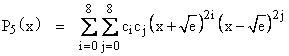Polynomials For Sums of Square Roots

For an arbitrary integer "a" the minimal polynomial with integer coefficients and possessing the root

can be found by squaring both sides to give

Of course, the other root of this polynomial is . 

If we are given two integers a,b and we wish to find a polynomial with integer coefficients whose roots include

we can simply square both sides to give

Subtracting a + b from both sides, squaring both sides again, and re-arranging terms gives the polynomial with integer coefficients

This polynomial is of degree 4, and it has the four roots give by any combination of the two signs in

Of course, the coefficients of the polynomial could also be expressed as the elementary symmetric functions of these four roots. The odd functions vanish identically, and the even functions are free of square roots.

If we are given three integers a,b,c and we wish to find a polynomial with integer coefficients whose roots include

we anticipate that the coefficients could be expressed as the elementary symmetric functions of the eight quantities given by every combination of signs for the square roots. However, it would be somewhat laborious to algebraically evaluate, say, the sum of all products of two of those quantities, and so on. As an alternative, we can proceed as before, first squaring both sides and re-arranging terms to give

Squaring both sides gives

Letting S₁ denote the first symmetric function a + b + c, and letting S₂ denote the second symmetric function ab + ac + bc, the above can be written as

Squaring both sides again gives

where S₃ denotes the third symmetric function abc. Noting that the term involving the radicals is given from equation (1) by x² - S₁, this gives the final polynomial

This is an even polynomial of degree 8 (meaning that all the coefficients of odd powers of x are zero), and as expected its roots are the eight values given by the eight possible combinations of signs in

The constant coefficient of the polynomial with these roots is always a square integer, namely the square of S₁² – 4S₂.

Now let's suppose we are given four integers a,b,c,d and we wish to find the minimal polynomial with a root equal to

For brevity, let s_j denote the jth symmetric function of the square roots of a,b,c,d, and let S_j denote the jth symmetric function of the full values of a,b,c,d.  Our objective is to operate on the expression x = s₁ until we have eliminated all the s_j terms and everything is expressed in terms of S_j values.  We can proceed as before, squaring both sides of the above to give

Subtracting S₁ and squaring both sides gives

Recalling that s₁ equals x, we can re-arrange terms to give

Squaring both sides again, and noting that s₄² = S₄, we have

Expanding s₃², we find

Making this substitution and moving all the S_j terms over to the left hand side, we have

We know the 2s₂ equals x² - S₁, and we also know from equation (2) that

Making these substitutions into the right hand side of the preceding equation and re-arranging terms to isolate the s₄ on the right, and squaring both sides again, we arrive at the following expression involving only S_j functions

where

This is an even polynomial of degree 16 (meaning that all the coefficients of odd powers of x are zero), and as expected its roots are the sixteen values given by the sixteen possible combinations of signs in

The constant coefficient of the polynomial with these roots is always a square integer, namely the square of

To illustrate, the quantity consisting of the sum of four square roots

is a root of the polynomial

The 16 roots of this polynomial are the values given by all 16 possible combinations of signs for the four square roots in the expression for x.  This is the minimal polynomial with integer coefficients having the stated value of x as a root.

As we proceed to sums of more and more terms, the explicit expressions for the minimal polynomials become extremely complicated, despite the fact that the coefficients are simply the elementary symmetric functions of the sums with all possible combinations of signs. As we’ve seen, for sums of just three square roots, the minimal polynomial has 2³ = 8 roots, and the total number of terms in all the elementary symmetric functions of those eight roots is 2⁸ = 256, so it is already not a very efficient way of trying to express the polynomial coefficients. For sums of four square roots, the minimal polynomial has 2⁴ = 16 roots, and the total number of terms in all the elementary symmetric functions of those sixteen roots is 2¹⁶ = 65536. This shows why the explicit expression for this polynomial given above is comparatively very succinct. But at the next step, considering sums of five square roots, the minimal polynomial has 2⁵ = 32 roots, and the total number of terms in all the elementary symmetric functions is 2³² = 4294967296. Thus the total number of terms is the exponential of an exponential, so it is squared on each successive level. In view of this, we can hardly expect to be able to write down explicitly the general polynomial for a sum of five square roots in terms of the elementary symmetric functions of the squares of those five quantities, as we did above for the lower-order cases.

Nevertheless, we can express the fifth-order polynomial in a certain way. Consider, for example, the coefficients of the polynomial whose roots are all the numbers of the form

where “e” represents a fifth integer. If we let P₄(x) denote the minimal polynomial with the sixteen roots given by (3), and if we let P₅(x) denote the minimal polynomial with the 32 roots given by (4), then clearly

The first factor on the right side has all the same sixteen roots as P4, but shifted by, and the second factor has the same 16 roots, but shifted by . Thus the product has the desired 32 roots represented by (4). The polynomial P₄ (as derived above) can be expanded and written in the form

Hence we have

From this we can see that P₅ is, as expected, an even polynomial with integer coefficients, because we can write the above summation as

The two binomials inside the square brackets have additive even-ordered terms and cancelling odd-ordered terms, so we get only even powers of x and  in the result.

Return to MathPages Main Menu