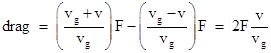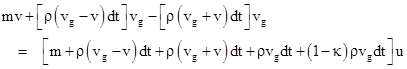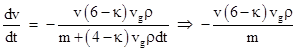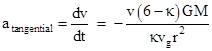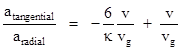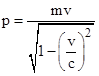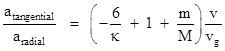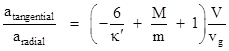Lesage's Shadows

The law of gravity formulated by Isaac Newton describes how massive bodies move under the influence of their mutual gravitation, but it doesn’t explain this influence in terms of any more fundamental processes. This prompted critics to charge that Newton conceived of gravity as an occult phenomenon (or “a perpetual miracle”). He answered that the phenomena of gravity are not occult, although their cause may be. Over the course of his life he seems to have entertained a variety of ideas about the possible cause of gravity, and whether it might be an intrinsic quality of matter. In 1693 he wrote to Richard Bentley

You sometimes speak of gravity as essential & inherent to matter; pray do not ascribe that notion to me, for ye cause of gravity is what I do not pretend to know, & therefore would take more time to consider of it… Tis unconceivable that inanimate brute matter should (without ye mediation of something else wch is not material) operate upon & affect other matter wthout mutual contact; as it must if gravitation in the sense of Epicurus be essential & inherent in it. And this is one reason why I desired you would not ascribe innate gravity to me. That gravity should be innate inherent & essential to matter so yt one body may act upon another at a distance through a vacuum wthout the mediation of any thing else by & through wch their action or force may be conveyed from one to another is to me so great an absurdity that I believe no man who has in philosophical matters any competent faculty of thinking can ever fall into it. Gravity must be caused by an agent acting constantly according to certain laws, but whether this agent be material or immaterial is a question I have left to ye consideration of my readers.

The parenthetical “without the mediation of something else which is not material” is difficult to reconcile with the rest of the quote, because the triple negative implies that the mediation must obviously be by means of something which is not material, whereas he concludes the passage by saying he does not know if the agent be material or immaterial. From his other writings, we can gather that he actually suspected the cause to be immaterial, specifically the will of God - but the above quote is often cited as evidence that Newton believed there must be a mechanistic explanation for gravity. In Query 21 in his treatise on Opticks, after discussing a possible Aetheral Medium for the propagation of light, he described one possible mechanism for gravity

Is not this Medium much rarer within the dense Bodies of the Sun, Stars, Planets and Comets, than in the empty celestial Spaces between them? And in passing from them to great distances, does it not grow denser and denser perpetually, and thereby cause the gravity of those great bodies towards one another, and of their parts towards the Bodies; every Body endeavouring to go from the denser parts of the Medium towards the rarer?

The idea of a fluid pressure as the cause of gravity was later taken up and elaborated by Euler (who admitted he was unable to explain why the pressure of the putative medium would be lower near massive objects). However, a few pages further on Newton categorically rejects any such Medium. In Query 28 he writes

Are not all Hypotheses erroneous, in which Light is supposed to consist in Pressions or Motion, propagated through a fluid Medium? … And for rejecting such a Medium, we have the authority of those the oldest and most celebrated Philosophers of Greece and Phonecia , who made vacuum and atoms and the gravity of atoms the first principles of their philosophy, tacitly attributing gravity to some cause other than dense matter.

Then in Query 31 he reverts to agnosticism, affirming that

How these attractions may be performed I do not here consider. What I call attraction may be caused by impulse, or by some other means unknown to me. I use that word here to signify only in general any force by which bodies tend toward one another, whatsoever be the cause.

The situation is complicated by the fact that the Queries are not presented in the order in which they were written. The middle Queries, containing Newton’s “pro-aether” ideas, were actually added in the last edition of Opticks, when Newton was 75 years old, and it’s been suggested that he inserted these comments only to appease the materialist critics. On the other hand, these Queries may have been based on some of his earliest writings in the 1670s (including a letter to Robert Boyle), which he only belatedly decided to preserve. Even in the year 1693, the same year as the letters to Bentley quoted above, Newton wrote to Leibniz arguing that mechanistic causes are to be rejected.

For since celestial motions are more regular than if they arose from vortices and observe other laws, so much so that vortices contribute not to the regulation but to the disturbance of the motions of planets and comets; and since all phenomena of the heavens and of the sea follow precisely, so far as I am aware, from nothing but gravity acting in accordance with the laws described by me; and since nature is very simple, I have myself concluded that all other causes are to be rejected and that the heavens are to be stripped as far as may be of all matter, lest the motions of planets and comets be hindered or rendered irregular.  But if, meanwhile, someone explains gravity along with all its laws by the action of some subtle matter, and shows that the motion of planets and comets will not be disturbed by this matter, I shall be far from objecting.

At about this same time, Newton’s friend Nicolas Fatio de Duillier proposed a mechanistic explanation of gravity in which an omni-directional flux of small particles permeates all of space and tends to push objects together because they mutually shield each other from this flux, but according to David Gregory “Mr. Newton and Mr. Halley laugh at Mr. Fatio’s manner of explaining gravity”. Based on lengthy discussions with Newton on this subject, Gregory wrote

The plain truth is that he [Newton] considers God to be omnipresent in the literal sense… but if this way of proposing his notion be too bold, he thinks of doing it thus: What cause did the Ancients assign of gravity? He believes that they reckoned God the cause of it, nothing else, that is no body being the cause, since every body is heavy.

It’s interesting to consider the reasoning behind the statement “no body being the cause, since every body is heavy”, which succinctly conveys the idea that even the material entities posited as the cause of gravity must themselves have weight (i.e., gravitational mass), which is paradoxical if they themselves are regarded as the mechanism of weight. We can see in this argument an early expression of the equivalence principle, i.e., the identity (not merely the equality) between inertial and gravitational mass. Any mechanistic theory of gravity based on classical dynamics implicitly denies this identity, because such a theory seeks to take inertia as fundamental and then to construct the appearance of gravity as a higher-order phenomenon. Instinctively Newton recoiled from this incongruity, guided by the (admittedly vague) impression that gravity and inertia are equally fundamental. At one point he even drafted a new set of corollaries to Proposition 6 of Book 3 of the Principia, culminating in

Corol 9: There exists an infinite and omnipresent spirit in which matter is moved according to mathematical laws.

which would place inertia and gravitation on an equal footing, but in the end he thought better of publishing this. (Shades of “the sensorium of God”.) Still, it’s fair to say that Newton remained ambivalent and non-committal about the cause of gravity. Of course, the “cause” of inertia was considered to be, if anything, even more problematic than the “cause” of gravity, as seen in the Leibniz-Clarke debate, so an explanation of gravity in terms of inertia would still rely on Newton’s suppressed ninth corollary.

It was Roger Cotes who, in his preface to the second edition of the Principia, expounded what came to be regarded as the Newtonian view - despite the fact that it conflicted with some of Newton's previous statements. (Whether Newton at this time endorsed the views in Cotes' preface is not known. Based on Newton’s character, it’s hard to imagine him allowing an edition of his masterpiece to be prefaced with sentiments he abhorred. On the other hand, when Cotes wrote to Newton that “I think it will be proper… to add something [to the preface] more particularly concerning the manner of philosophizing”, Newton was so wary of controversy that he replied “If you write any further Preface, I must not see it, for I find that I shall be examined about it.”) Cotes was quite prepared to accept the idea of gravity as an elemental and intrinsic attribute of matter, not in need of (or capable of) being described in any more fundamental terms.

I can hear some people disagreeing with this conclusion and muttering something or other about occult qualities. They are always prattling on and on to the effect that gravity is something occult, and that occult causes are to be banished completely from philosophy. But it is easy to answer them: occult causes are not those causes whose existence is very clearly demonstrated by observations, but only those whose existence is occult, imagined, and not yet proved. Therefore gravity is not an occult cause of celestial motions, since it has been shown from phenomena that this force really exists. Rather, occult causes are the refuge of those who assign the governing of these motions to some sort of vortices of a certain matter utterly fictitious and completely imperceptible to the senses.

But will gravity be called an occult cause and be cast out of natural philosophy on the grounds that the cause of gravity itself is occult and not yet found? Let those who so believe take care lest they believe in an absurdity that, in the end may overthrow the foundations of all philosophy. For causes generally proceed in a continuous chain from compound to more simple; when you reach the simplest cause, you will not be able to proceed any further. Therefore no mechanical explanation can be given for the simplest cause; for if it could, the cause would not yet be the simplest. Will you accordingly call these simplest causes occult, and banish them?

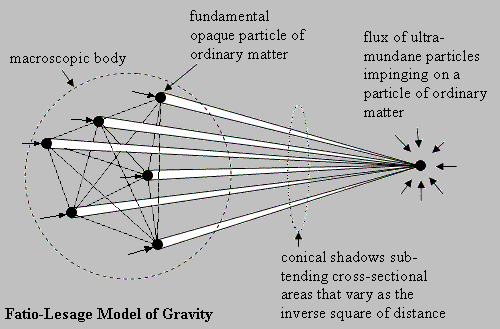
With the success of Newton’s system the idea of force at a distance as a primary attribute of matter gradually became the dominant paradigm of physics, although there were still attempts to conceive of "underlying" physical processes that could account for the effects of gravity. Typically these attempts accepted Newton's laws of mechanics as fundamental, although it's unclear why the phenomenon of inertia should be considered any more fundamental than the phenomenon of gravity. (Note that there have also been relationist attempts to explain inertia as a manifestation of gravity, ala Mach.) One of the most famous of the attempts to identify a mechanism for gravity was the "shadow theory" proposed by Georges-Louis Lesage (1724-1803), who is usually credited with building one of the first telegraphs. (His telegraph had 26 wires, one for each letter of the alphabet.) Like Fatio a century earlier, Lesage suggested (in his 1782 paper Lucrece Newtonien) that space is filled with an omni-directional radiation field consisting of tiny particles - which Lesage later, in papers published by Pierre Prevost, called "ultra-mundane particles" (literally, super-natural or other-worldly particles, “because they traverse the universe, and therefore come from outside the natural world”) moving at very high speed in all directions, and with an extremely great mean free path. In other words, although these ultra-mundane particles cross each others’ paths, they do not appreciably interact or interfere with each others motions.

The gravitational corpuscles are isolated, so that their progressive movements are necessarily rectilinear… They are so thinly scattered—that is to say, their diameters are so small relative to their mutual mean distance—that there are no more than a few hundreds which encounter one another in the course of a thousand years. Hence the uniformity of their movements is never sensibly disturbed… They move in several thousand of thousands of different directions… separated from one another by less than a second of arc… Parallel to each of these directions [at every point in space] there moves a stream or torrent of corpuscles.

According to Lesage, massive bodies intercept and absorb a (small) fraction of the gravitational corpuscles striking them, so they cast shadows in all directions. If two massive bodies are brought close together, they partially shield each other from the radiation, resulting in a net force on each body toward the other. (In asserting that the corpuscles are absorbed whenever they strike ordinary matter, Lesage differed from Fatio, who had argued that the corpuscles are reflected, albeit at a lower speed than their incident speed. As explained in the note on omni-directional flux, Fatio’s mechanism was actually more efficient than Lesage’s, and based on more sophisticated reasoning.)

Since the angular area subtended by an object at a distance r drops in proportion to 1/r², for values of r much greater than the size of the object, it’s clear that the fraction of the incoming radiation blocked by a given opaque object at a given point is also proportional to 1/r², so we immediately get (for any body composed of tiny opaque entities) an isotropic force that varies essentially as the inverse square of the distance (on the scale of the mean free path length of the ultra-mundane particles). Of course, in order to give a force that is proportional to the mass rather than to the size of an object, and to explain why saturation does not occur, i.e., why there is no apparent depletion of the capacity for gravity in the vicinity of massive bodies, we must suppose that macroscopic bodies are almost perfectly transparent to the ultra-mundane particles, so only a tiny fraction of the particles passing through an object are actually intercepted. We must also assume the particles of matter are so small relative to their mutual separations, and the particles are arranged so irregularly, that the total projected opaque area (in any direction) is essentially equal to the sum of the area of the individual elementary particles. This enables us to say the force is proportional to the number of particles in a body rather than to the size of the body, and it also avoids the saturation problem (up to some level of precision).

As for the constitution of heavy objects, Lesage asserted that

Their indivisible particles are cages; for example, hollow cubes or octohedra. (They are, in other words, skeletons of solids of which there is nothing material except the edges.)

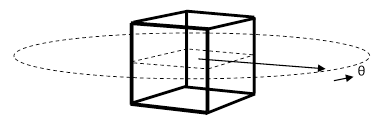
This feature of Lesage’s theory is rather unhelpful, because thin bars connecting the vertices of a cube (for example) present a cross-sectional area that varies as a function of orientation θ in the orthogonal plane, as shown below

Charitably neglecting the singular orientation when bars completely shadow each other, the projected area of the twelve bars in the direction θ is

Thus if we take Lesage’s skeletons as the fundamental particles of matter, we need to make the further stipulation that they are arranged and oriented within macroscopic bodies in a totally irregular way, so that the anisotropy inherent in each skeleton averages out for large aggregates. This is an unnecessary and useless complication, since we can simply assume the elementary particles are tiny spheres, which are inherently isotropic. Of course, in either case, we still have the problem of arranging the elementary particles with sufficient irregularity so that they have virtually no overlap when viewed from any possible direction (not to mention the problem of constraining them to maintain their shapes and relative positions without the benefit of an elemental force of attraction), but with spherical particles we at least need not worry about scrambling the orientations of inherently anisotropic elements.

So, taking simple spheres as the elementary particles of heavy matter, a rough illustration of the Fatio-Lesage model of gravity is shown below.

Here we’ve shown links to denote the forces holding the elementary particles of matter together in the macroscopic body in an irregular pattern. These links are not explained in Lesagean theory, although they are essential to provide the forces of both attraction and repulsion required to maintain the structural stability of macroscopic bodies. As noted above, Lesage says the elementary particles are skeletal structures, but he doesn’t say how these cubes or octahedrons are linked together; we know it cannot be in any regular lattice pattern because that would result in anisotropic gravity. Even if we allowed “bars” to link the elemental particles together in some irregular manner, it still would not explain how these bars exert attractive force. Thus, even within its own premises, the Fatio-Lesage theory necessarily invokes the action of unexplained attractive forces. This gives the entire theory a certain childlike quality, which is perhaps not surprising, considering that although he was 58 when he published his theory, Lesage tells us he conceived it in his childhood.

I did not take undue credit to myself when as a child I rectified the system taught by Lucretius and drew from it immediately its most important consequences, for this was extremely easy or rather entirely natural. Besides, I knew but little more the value and solidity of my little views than the child ordinarily knows the wit or sense which we find in its repartees and sallies.

It’s worth noting that Lesage’s omni-directional flux of ultra-mundane particles does not comprise a fluid in the normal sense of the word, it is an entirely different concept. (Fluid sinks have actually been proposed as models of gravity, but they operate on an entirely different principle.) In a fluid, contiguous elements are in equilibrium with each other, whereas in the Fatio-Lesage radiation field there are streams (indeed, torrents!) of ultra-mundane particles moving arbitrarily close to each other and crossing paths in all directions. The state of this omni-directional flux is the conceptual opposite of thermodynamic equilibrium. Lesage himself was at least partly aware of what a radical concept this is. As to why no one previously had thought of this explanation for gravity (as far as he admitted knowing, despite having collected Fatio’s papers), he wrote

Doubtless because the most of them having no clear view of this chaos (of which the first glance is, I admit, frightful) they have not known how to disentangle it and subject it to their calculations.

Indeed the prospect of millions of independent torrents of particles streaming in different directions through every point in space, all without disturbing each other, almost makes the “many worlds” interpretation of quantum mechanics look parsimonious. On the other hand, to be fair to Lesage’s childhood inspiration, we now know that the atoms and molecules comprising ordinary matter actually do consist of very tiny particles in mostly empty space (neglecting the fields), which makes it possible for very weakly interacting particles like neutrinos to pass through the entire Earth (for example) quite easily. The “transparency” of matter can, with some justification, be regarded as a prediction of the Fatio-Lesage model, since the atomic structure of matter was unknown when the model was first put forward.

However, other features of Lesagean theory conflict rather badly with what is now known about the structure of matter. According to Lesage’s theory we can have equality between inertial and gravitational mass only if all matter consists of identical elemental opaque entities (i.e., entities of exactly the same size, shape, and inertial density) in exactly the same proportion, whereas we now know that different kinds of material substances consists of different combinations of protons, neutrons, and electrons. Furthermore, we now know that both the inertial and the gravitational masses of these substances depend on their binding energy as well as the number of elementary particles they contain, and indeed we know that even pure energy (light) is affected by gravity precisely in accord with the equivalence principle. All these facts are inherently incompatible with the Lesagean model of gravity. Any suggestion that we can restore inertial and gravitation equivalence to Lesage’s model by regarding protons, neutrons, and electrons as composite bodies formed from a single species of identical opaque particles merely introduces another layer of structure, requiring still more unexplained elementary attractive forces to maintain it – the very thing Lesagean theory is intended to obviate.

Still, setting aside the fundamental incompatibility between Lesagean theory and the stability of matter, we can proceed to assess some other implications of such a theory, based on the assumption that macroscopic matter is composed of a very sparse aggregate of fundamental opaque spherical particles with identical size and inertial mass (or, if there are different sizes, they must be combined always in the same proportions in macroscopic bodies), and with the assumption that these particles do not align themselves in such a way as to alter their combined gravity. These assumptions then impose further requirements. The inverse-square property depends on the ability of the omni-directional flux of ultra-mundane particles to maintain the shadowing effect in strict proportion to the angular extent of the image of an elementary opaque particle as the distance increases. Clearly the ultra-mundane particles can impart momentum to massive objects only to the extent that they are absorbed, because any reflected ultra-mundane particles would not contribute to the shadowing effect. Also, the ultra-mundane particles must not interact with each other at all, because the slightest interaction would smudge out the shadow effect and thereby destroy the inverse-square relation. But in a mechanistic context the particles must still have some finite density (particles per volume), so there is a limit to the resolution of the shadow image that can be maintained.

At some finite distance from a fundamental opaque particle of ordinary matter its image will become indistinguishable from a point, by which time the inverse-square relation will have been totally lost. (Some benefit could be gained for large macroscopic aggregates by averaging the shadows of a large number of particles, but only if we posit that the particles are not all subjected to exactly the same acceleration, which then represents another mechanism of heat generation and entropy increase, and in any case, it is still necessary for the radiation field to have extraordinary angular resolution, as Lesage himself acknowledged.) This characteristic distance is proportional to the size of the fundamental opaque particles of matter, which we have already seen must be extremely small in order to make the force of gravity proportional to the number of particles (i.e., the mass) of macroscopic bodies and to avoid the saturation problem. But the smaller we make the fundamental particles of matter, the shorter becomes the distance to which the inverse-square relation will hold for a given density of ultra-mundane particles. In essence, the radiation field of Lesagean particles must be dense enough (and free enough from self-interaction) to resolve the angular radius of a particle the size of an electron from hundreds of millions of miles away! Thus, to maintain the inverse square relation for any appreciable distance, we need to assume the field of ultra-mundane particles has virtually infinite density (i.e., particles per unit volume), and this density must be angular as well as translational. In other words, we require not only a virtually infinite flux of ultra-mundane particles per unit area, we also require this flux to be coming from all directions with virtually infinite angular resolution. Then, in order to avoid interacting with each other, each of these ultra-mundane particles must have essentially zero cross-sectional area.

Accepting for the moment that all these rather daunting requirements are met, and accepting the combined rationalizations regarding the densities and sizes of weighty particles, there are still some serious problems for shadow gravity, many of which can be traced back to the finite speed of the ultra-mundane particles. As a macroscopic body moves (relative to the frame with respect to which the ultra-mundane flux is isotropic) it will naturally encounter more particles on its leading face than on its trailing face, resulting in a net drag on the body. Quantitatively, if a series of equally-spaced ultra-mundane particles with speed v_g are impinging on a stationary opaque object from two opposite directions, the object will be struck by particles at the same rate on both sides. (How all the independent ultra-mundane particles acquired this particular speed is not explained.) However, if the object moves with speed v in one direction along this axis, the rate of encountering particles on its leading face is increased in the ratio (v_g + v)/v_g, and the rate of encountering particles on its trailing face is decreased in the ratio (v_g – v)/v_g, so the original force balance F – F = 0 becomes

The momentum transferred to an object by each ray of flux must be large enough to account for gravity, which implies that F in the above equation is not negligible. Since we do not observe any appreciable drag on (for example) the planets in their orbits around the Sun, we must impose some further restriction on the model to minimize this effect. To minimize the drag we must assume the speed v_g of the ultra-mundane particles is extremely great. Thus, we find once again that a natural consequence of the model must be nullified by setting one of the parameters to an extreme value.

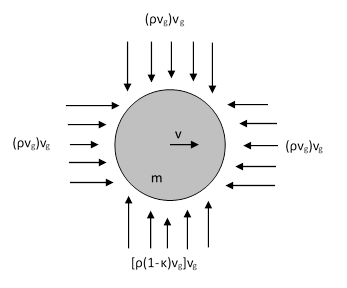
To treat this more fully, let ρ denote a measure of the spatial density of the ultra-mundane particles absorbed by ordinary matter, defined such that ρUdt equals the quantity of mass accretion by a sphere of a given radius from a given direction in an increment of time dt, where U is the relative speed between the ultra-mundane particles and the sphere along that direction. For a massive sphere in orbit around some center of mass with another body we will consider just the radial and tangential flows as shown below.

The radiation density from the bottom (i.e., from the direction of the other orbiting body) is reduced by the factor (1–κ) where κ is a small number representing the fraction of the flux that was intercepted by the neighboring body. (Note that, since the gravitational constant does not change appreciably with distance from the Sun, we know that κ for the Sun must be no greater than one part in a hundred million, i.e., 10^–8). Beginning with a mass m and speed v, the orbiting body will absorb in an increment of time dt ultra-mundane particles with momentum in the horizontal direction equal to [ρ(v_g–v)dt]v_g and –[ρ(v_g+v)dt]v_g. The mass accreted from particles in the horizontal direction is equal to the quantities in the square brackets. In addition, during this same increment of time, the object will accrete from particles in the vertical direction quantities of mass equal to [ρ(v_g)dt] and [(1–κ)ρ(v_g)dt]. Letting u denote the horizontal speed of the object at the end of this increment of time, the conservation of momentum requires

Solving this for u, subtracting v, and dividing by the incremental time dt gives the rate of change of speed (i.e., the acceleration) in the horizontal direction

We also know that the slight different in the radiation density in the vertical direction produces the force of gravity on the object, so we have

where M is the mass of the other gravitating body and r is the distance between the bodies. Solving this for the density ρ and substituting into the previous equation gives the acceleration due to drag

The radial acceleration is of course GM/r², so the ratio of the tangential to the radial acceleration is

The second term represents the effect of Bradley aberration resulting from the fact that the planet is moving perpendicularly to the incoming shadow, so vector addition causes the apparent direction of the shadow (i.e., the “attractive force”) to be slightly forward of the actual direction. This effect should not be confused with the aberration resulting from the motion of the source body during the finite time required for the shadow to traverse the distance between the source and the planet, which will be discussed below.

In order for the orbits of the planets around the Sun to have persisted for hundreds of millions of years, the ratio of tangential to radial acceleration can be no greater than about 10^–10, and we’ve already noted that the fraction κ of ultra-mundane particles absorbed by the Sun can be no greater than 10^–8, so the above relation implies that the speed of the ultra-mundane particles must be at least (6)10¹⁸ times the speed v of the planet. The planet Mercury has an orbital speed of about (4.8)10⁴ m/sec, so the value of v_g must be at least (2.9)10²³ m/sec, which is about 10¹⁵ times the speed of light. Henri Poincare used more stringent limits on the shielding and acceleration ratios to conclude that v_g must be about 10¹⁷ times the speed of light. In any case, it’s clear that the gravific corpuscles must be assumed to move at a speed far in excess of the speed of light. This may not have been considered an impossibility in the time of Fatio or Lesage (or even in the time of Kelvin and Maxwell), but it is surely known to be impossible today. This is true regardless of whether one adopts the Einsteinian or the Lorentzian interpretation of special relativity because, in either case, the momentum of a corpuscle of (rest) mass m moving with speed v is not p = mv but rather

The modern laws of mechanics are solidly based on this fact, which has been confirmed to phenomenal accuracy by countless observations. In order to even begin to make any rational sense of a Lesage theory, we must be able to quantify the momentum (and hence the imparted impulses) of the ultramundane corpuscles, but if we assign them velocities much greater than c, the momentum is imaginary. It is not at all clear what would be the result of a collision between a superluminal corpuscle with imaginary momentum and a sub-luminal particle of ordinary matter with real momentum. This obviously requires a completely new kind of “mechanics”, because according to the known laws of mechanics it is a non-sensical proposition. Without pre-judging whether a new science of mechanics could be devised to make sense of particles with imaginary momentum, we can certainly say that Lesage’s theory is flatly incompatible with the presently known and accepted science of mechanics. Since the whole purpose of Fatio-Lesage theory was to “explain” gravity in terms of the known science of mechanics, it would be self-defeating to try to salvage the theory by appealing to a completely new and presently unknown science of dynamics.

Setting aside the fundamental conflict with special relativity and the modern science of mechanics, the extremely high speed of the corpuscles would imply that the effective “temperature” of the flux is incredibly high, and the flow of energy from the flux into ordinary material bodies (like the planets) would be so great as to vaporize them in a fraction of a second. Maxwell had previously made a similar argument. In simple terms, the momentum of a particle of mass m is mv, whereas the kinetic energy is mv²/2, so the ratio of energy to momentum is v/2. Consequently, in order for the ultra-mundane particles to impart a given amount of momentum to an ordinary massive object (such as a planet) by being absorbed or slowed by the object, the corresponding energy absorbed by the object increases in direct proportion to the speed of the ultra-mundane particles.

Quantitatively, Lesage’s theory implies that the ultra-mundane particles impart enough momentum to a planet of mass m_p moving in a circular orbit with speed v_p to completely reverse it’s direction every half revolution. Thus its momentum changes from +m_pv_p to  –m_pv_p, for a total momentum change of 2m_pv_p every half revolution, or 4m_pv_p per revolution. This momentum is imparted by absorption of ultra-mundane particles with total mass m_u and speed v_g such that m_uv_g = 4m_pv_p. The kinetic energy E = (1/2)m_uv_g² of these ultra-mundane particles is also absorbed by the Earth. (We exclude reflected particles from consideration because, as shown in Omni-Directional Flux, any reflection combined with absorption would cause the gravitational forces exerted by two bodies on each other to be unequal, assuming passive and isotropic interactions consistent with a kinetic model.) Substituting from the momentum equation to eliminate m_u, we get E = 2m_pv_pv_g. By Kepler’s third law we also have Gm_s = ω²r³ = v_p²r, where G is the gravitational constant, r is the radius of the planet’s orbit, ω is the angular speed of the planet, and m_s is the mass of the Sun. The period of the orbit and the speed of the planet are therefore given by

Substituting into the equation for the energy per revolution and dividing by the period of one revolution gives a lower bound on the energy per second absorbed by the planet

For the Earth and Sun we have

so if we assume the speed of the ultra-mundane particles is just v_g = c = (3.00)10⁸ m/sec we find the rate at which energy is being added to the Earth due to collisions with the ultra-mundane particles must be at least

For comparison, the entire energy output of the Sun is (4)10²⁶ J/sec, so Lesage’s theory requires us to believe that the Earth is continually absorbing about 8500 times the Sun’s energy output – and this refers not just to the fraction of the Sun’s energy that strikes the Earth, but to the entire Sun’s output! This is based on the relatively mild assumption that the ultra-mundane particles move at “only” the speed of light. If, as Laplace estimated in order to avoid aberration problems, the speed of these particles is really a million times greater than the speed of light, the energy flow increases by the same factor. Even worse, if we take Poincare’s estimate that v_g must be at least 10¹⁷ times the speed of light to avoid excessive aberration (to be discussed below), then the Earth must be absorbing energy at a rate of at least 10²¹ times the Sun’s total output rate.

We stress that these represent absolute lower bounds on the amount of energy that must be absorbed by a planet consistent with the observed transfer of momentum. Notice that we have actually accounted only for the energy corresponding to the unbalanced momentum imparted to the object. We know each object is actually struck by a huge number of particles from all directions, and the net force of gravity is just due to the relatively small macroscopic imbalance between the number of particles striking the object from various directions. If even a tiny fraction of the balanced flux of ultra-mundane particles smashing into ordinary bodies are absorbed, they contribute still more vast amounts of energy to the bodies. We also know that the ratio of total collisions to unbalanced collisions is enormous, because it is 1/κ along the direction of the Sun, and this must be multiplied by all the axes along which particles are bombarding the planet equally in both directions. The Sun subtends about 2 angular degrees of arc when viewed from the Earth, so that two-sided cone covers only about 1/6566 of the directional axes. Thus the total number of collisions must be at least (6.5)10¹¹ times the number of unbalanced collisions. If even a tiny fraction of this balanced flux is absorbed, the energy transfer would dwarf the already inconceivably huge energy transfer associated with the unbalanced flux. But how is this distinction between balanced and unbalanced to be enforced? An elemental opaque particle of ordinary matter is struck on its left and right sides by two fluxes of ultra-mundane particles, of very slightly different intensity, and we are required to believe that all the collisions from the weak side are reflected, and an exactly equal amount of the flux on the strong side is reflected, so only the imbalance from the strong side is absorbed. The term “perpetual miracle” comes to mind. (For improved lower bounds on the energy flux implied by the Fatio-Lesage theory, taking into account the total rather than just the net momentum, see the note Omni-Directional Flux.)

We should also mention that the shower of ultra-mundane particles must be dense enough so that each individual elementary particle of ordinary matter is being struck almost continuously in the correct ratio from all directions, because if we imagined the particles of ordinary matter being struck only occasionally by an ultra-mundane particle from one direction or another, the fantastic energy of each collision would, if unbalanced by an opposing collision, knock the elementary particle out of the body. Thus the shower of ultra-mundane particles must be nearly continuous not just on the scale of macroscopic objects but on the scale of the elementary opaque particles of ordinary matter.

In 1873 William Thomson suggested a way around the energy problem, by assuming the ultra-mundane particles serve two functions. First, they transfer their linear momentum to the object. Second, they carry away the excess heat in the form of rotational or vibratory energy. In other words, he suggested that the ultra-mundane particles strike the object with high translational speed and momentum but no intrinsic spin or vibration, and then are shed with low translational speed, low linear momentum, but spinning and/or vibrating very rapidly. Of course, in the case of spin, if we are to conserve angular momentum we must also assume the ultra-mundane particles are spun in pairs with equal and opposite spins, or else each individual particle consists of parts that can spin in opposite directions. Alternatively we could assume each ultra-mundane particle possesses an intrinsic vibrational mode that can absorb energy.

However, there are serious problems with the idea of relying on the ultra-mundane particles to absorb and carry off energy in either rotational or vibrational modes. As discussed above, in order to satisfy other requirements, the ultra-mundane particles must not interact with each other, so any energy modes they possess must be intrinsic to each individual particle, not to aggregates of two or more particles. This implies that Thomson’s ultra-mundane particles must not only carry translational momentum, they must possess an internal structure, with spatially separate “parts” held together by some very strong force, in order to absorb energy in a mechanistic way (regardless of whether the mode is assumed to be rotational or vibratory or any combination of those). Thus, in attempting to salvage Lesage’s theory, Thomson is compelled to posit primitive attractive forces (i.e., attractions not resulting from kinetic impulses), the very thing Lesage theory was intended to obviate. The force of attraction holding the parts of each ultra-mundane particle together can have no mechanistic explanation – unless we wish to propose a meta-field of ultra-ultra-mundane particles, leading to an infinite regress.

Even if we are willing to sacrifice the original purpose of the theory in our efforts to save it, there remain other difficulties with Thomson’s approach. Admittedly, the ultra-mundane flux is not in thermodynamic equilibrium with itself, let alone with the universe of ordinary matter, so we cannot argue that the kinetic energy must be equally partitioned between the various available modes. As a result, one can conceive of a (albeit highly artificial) class of interactions and particle properties that would permit the conveyance of momentum from a set of high-speed (“hot”) particles to a set of low-speed (“cold”) particles without any significant transfer of heat from hot to cold. However, this requires the relatively large and cold particles to be both elastic and devoid of internal energy modes, whereas the small hot (ultra-mundane) particles must be inelastic with many internal energy modes. Furthermore, the mutual speeds of interaction must be tuned to precisely match the interaction threshold, such that an ultra-mundane particle can convey its momentum to a particle of ordinary matter, and then terminate the interaction and be released when it has absorbed an appropriate amount of energy. This is reminiscent of Maxwell’s demons, working furiously on each ultra-mundane particle to facilitate the required transactions – a concept that is about as far from a realistic mechanistic explanation as one can imagine.

Incidentally, Thomson correctly noted that, on the basis of Le Sage’s theory, it is possible to construct a perpetual motion machine. The basic idea is that the impenetrable constituents of an ordinary object could, in principle, be aligned closely in coherent rows so as to shield one another from the ultra-mundane flux in certain directions. The force of gravity on such an object near the Earth would (according to Le Sage’s theory) depend appreciably on the object’s orientation. For example, an object could weigh 10 pounds in one orientation, but only 9 pounds in another orientation. Placing the object in its lighter orientation, we could raise it to a height of one foot with 9 foot-pounds of work. We could then re-orient the object (with only a small effort that does not depend on the height) to its heavier orientation, and allow it to drop back down to its original position, yielding 10 foot-pounds of work. Thus the cycle has produced 1 foot pounds of “free” work, and this could be repeated indefinitely. (It’s interesting to compare this with the process described by Penrose for extracting energy from a gravitational black hole.)

It might be argued that Thomson’s process is not strictly a perpetual motion machine, because it is merely extracting work from the ultra-mundane corpuscles, and so the energy of the gravitational flux has been diminished by an amount equal to the work extracted. However, Thomson went on to suggest that the slow-moving and rapidly spinning (or vibrating) ultra-mundane particles, after colliding with matter, were re-habilitated into fast-moving non-spinning particles by interaction with the other ultra-mundane particles. This was not really necessary, since we could assume (as did Lesage) an infinite supply of “fresh” ultra-mundane particles from beyond the known universe, but Thomson was interested in the long-term cosmological implications for a process confined to our universe. Arguing for the plausibility of the re-habilitation process, he appealed to a principle enunciated by Clausius to the effect that the ratio of rotational to translational energy in a system of interacting particles at equilibrium remains constant. Of course, one pre-requisite of a Lesagean theory of gravity is that the ultra-mundane particles do not interact with each other and are not in equilibrium, i.e., they do not behave like the particles of a gas in equilibrium, at least not on the scale on which gravity acts as an inverse-square force. But on the cosmological scale, the self-restorative process suggested by Thomson effectively completes his perpetual motion machine. Since he had already shown how work could be extracted from the low-entropy flux, it would clearly violate the laws of thermodynamics for the flux to spontaneously restore itself to it’s original condition. In particular, it violates the second law of thermodynamics, because the pure streams of high speed translational ultra-mundane particles have lower entropy then the meandering and internally agitated ultra-mundane particles that are shed after colliding with ordinary matter. This is a highly irreversible process, to which the principle of Clausius is not applicable, so Thomson’s plausibility argument is invalid.

It has also been suggested that Lesage’s ultra-mundane particles could be replaced with waves of some kind, but this doesn’t significantly alter the situation. It is still necessary for ordinary matter to absorb “primary waves” and then shed the excess energy in the form of “secondary waves”, emitted uniformly in all directions, and these secondary waves must be even less interactive with ordinary matter than are the primary waves. Again, no one has ever proposed a plausible mechanistic explanation for how these gymnastics could be performed.

As mentioned above, the only interactions consistent with the principles of a kinetic model are passive and isotropic. We might, however, attempt to avoid the energy problem by postulating active non-isotropic reflection, conditioned by absorption. The concept is similar to the behavior of semi-conductors, which act as insulators when no voltage is applied, but which become conductors when a small voltage is applied. Similarly we might imagine that the reflectivity of a material object in any given direction is proportional to the absorption from that direction. The constant of proportionality could be arbitrarily great, so the object acts as an amplifier. A small imbalance in the flux density (due to the presence of another body nearby) could then produce a large anisotropy in the reflectivity of the basic structures of matter, like tiny one-way mirrors. This anisotropic reflectivity could then result in large transfers of momentum from the ultra-mundane flux to material objects, without requiring the absorption of large amounts of energy. However, actively anisotropic reflectivity requires the expenditure of energy, since otherwise it violates the second law of thermodynamics. Essentially each particle of matter must act as a Maxwellian daemon. Taking this into account, the concept is essentially equivalent to Thomson’s re-radiation proposal, except that is relies on an even less plausible mechanism, involving a highly complex set of attributes for the elementary constituents of matter. It might be interesting to study the consequences of such a model, but the abstractness and lack of conventional realism in such a model would surely be anathema to the proponents of Lesagean theories.

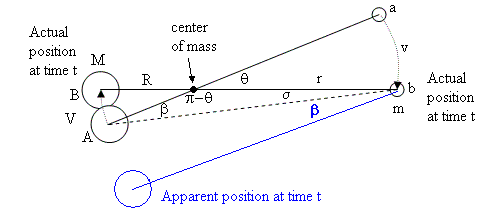
Even if we accept active anisotropic reflection or secondary re-radiation as ways around the energy problem (similar to accepting “Maxwell’s daemon” as a way around the second law of thermodynamics!), the finite speed of the ultra-mundane particles (or waves) poses additional problems, namely, drag and aberration. These problems are especially acute if we set v_g to “just” the speed of light. Drag and aberration both tend to upset the stability of planetary orbits. Proponents of Lesage theories sometimes argue that these two effects can compensate for each other, but this is not the case. To understand why, consider the simple two-body system shown below.

Let m and M be the masses of the two bodies, with radial distances r and R from the center of mass, and orbital speeds v and V respectively, and let v_g denote the finite speed of the Lesagean particles. Clearly we have m/M = R/r = V/v.

The total “aberration” between the actual and the apparent positions of the mass M as seen from the mass m is due to two causes. First, there is the “Bradley effect” discussed previously. This is the same effect that produces aberration of the apparent positions of stars as seen from the Earth. The vector combination of the speed v of the mass m perpendicular to the direction of the incoming rays with the speed v_g from the mass M results in a shift in the apparent position of M by an angle of approximately β = v/v_g. It’s worth noting that, for a shadow theory, the force carrying particle emanating from the source is actually a “bubble”, i.e., a missing particle that fails to offset the force applied by a particle coming from the opposite direction. Thus the Bradley component of aberration tending to pull the planet forward is actually a reduction of the drag tending to slow the planet. Since this is necessarily only a small fraction of the total drag, it obviously can never completely compensate for the drag.

The second cause of aberration is the fact that the incoming rays striking the mass m at a given time did not originate at the mass M at that same time, but rather at the mass M at an earlier time. Thus the true direction of the incoming rays is offset from the true current position of the mass M by the angle σ, which is approximately equal to V/v_g (because the sine of that angle is roughly the distance from A to B divided by the distance from A to b, and this is in the same ratio as the speeds). Thus we have the total aberration angle

For the smaller of the two bodies this effect is smaller than the Bradley aberration, which we’ve already seen is much too small to compensate full for the drag, so the combined aberration cannot compensate full for the drag. On the other hand, for the larger of the two bodies the predominant effect is due to the second cause. For example, the Sun has very little tangential speed relative to the incoming shadow cast by the orbiting planet, so the reduction in drag is very small, but the planet moves a significant distance from the time it casts the shadow to the time the shadow reaches the Sun, so this is the significant component of aberration.

Using the small-angle approximation with α in place of sin(α), the overall ratio of tangential to radial acceleration, accounting for drag and both kinds of aberration, is

This shows that we can make the tangential acceleration arbitrarily small by increasing v_g, but we cannot come close to negating the drag with the aberration. The same applies for the larger of the two bodies. Remembering that v = (M/m)V and noting that the appropriate value of κ to use when the small mass m is regarded as the source is κ′ = (m/M)κ, we have

(Of course, for the larger of the two orbiting bodies the absolute values of the accelerations are much smaller, but the ratio is the same.) These relations show that the idea of avoiding the energy problem by assuming a value of v_g near the speed of light, and using drag to compensate for aberration, doesn’t work, because the drag effect is necessarily many orders of magnitude greater than the aberration effect. The only way to minimize the orbital instability is by choosing v_g large enough that the tangential acceleration is negligibly small.

Incidentally, some neo-Lesageans (of the crackpot variety) have suggested that the motion of the planets through the radiation field of ultra-mundane particles imparts a “swirl” to the field, thereby reducing or eliminating the drag. Needless to say (or so one would have thought), this suggestion is totally incompatible with the most basic pre-requisites of Lesagean models, because a radiation field gives something like an inverse-square force only over distances comparable to the mean-free path of the radiation particles. Any interaction between particles destroys the inverse-square relation. Now, since the inverse-square relation holds good at least on the scale of the solar system, we know the mean free path of the ultra-mundane particles exceeds the diameter of the solar system, which implies that virtually all the ultra-mundane particle traverse straight through the solar system without striking anything. Thus there can be no "swirl" of the radiation field. (Of course, the speed of the ultra-mundane particles is many orders of magnitude greater than the speed of the planets, so on the time scale of the ultra-mundane particles the planets are virtually stationary, which implies that they could have no "swirling" effect on the radiation field, even if a significant fraction of the ultra-mundane flux interacted with the planets - which it doesn’t). These neo-Lesageans are obviously confusing Lesage’s particle radiation model with the fluid sink model.

We mentioned previously the problem of infinite regress for the forces of attraction holding the ultra-mundane particles together. Naturally the same problem applies to the structures of ordinary macroscopic objects. In fact, the very existence of stable macroscopic objects is a problem, because one of the basic premises of a Lesagean theory is that forces are to be understood solely in terms of inertial motions and collisions between particles, which implies that all forces must be reducible to “pushes”. The problem then is to account for the stability of macroscopic bodies, conceived as extremely sparse configurations of inertial particles. These particles may bounce off each other, but this will just cause them to disperse. No combination of bouncing (i.e., repelling) interactions alone will result in a stable coherent configuration of particles in the shape of, say, a penny. Needless to say, we cannot claim macroscopic objects are held together by gravity, because the forces needed to hold macroscopic bodies together and maintain their various shapes must be vastly stronger than the force of gravity. Again we might propose a field of “ultra-ultra-mundane” particles to supply these forces, but then we have the problem of explaining why this ultra-gravity doesn’t manifest itself on the scale of gravity, and also what maintains the spacing between elementary particles of matter. Just as serious is the problem of explaining how the elementary particles themselves, being of non-zero spatial extent, are held together. If we were to propose a Lesagean explanation for this, positing that these particles are not really elementary but are comprised of still smaller elementary particles held together by mutual shielding of a super-mundane radiation field, we would find ourselves in another infinite regress. Of course, the stability of composite arrangements of matter is difficult to explain on the basis of any classical dynamical interactions, even if we allow classical attractive forces at a distance. The stability of a hydrogen atom, for example, has so far been explained only in terms of quantum mechanics combined with the concept of attractive force fields.

Lesage himself recognized this fundamental problem, and this is why he suggested (as mentioned above) that ordinary macroscopic bodies are constructed like “cages”, i.e., a lattice network of tiny inter-connected bars. The idea was that the lattice was sparse enough to be virtually transparent to ultra-mundane particles, but still could maintain the structure of macroscopic bodies. This scheme may distract some critics, but it does nothing to actually solve the problem, because the bars of the cages obviously must have tensile as well as compressive strength, so each of them represents an elementary attractive force, which is precisely what the shadow theory is supposed to do without. The fact that the attractive forces maintaining the shapes of macroscopic objects cannot be given a consistent Lesagean interpretation seriously undermines the cogency of any Lesagean model for apparently attractive forces (even if the model wasn’t already ruled out on the basis of aberration and energy considerations). Moreover, the standard model of elementary particles (electrons, protons, neutrons, etc.) that has emerged during the last century is not at all consistent with the requirements of a Lesagean interpretation of gravity. Indeed we now know that even the binding energy of configurations of elementary particles contributes to the weight of those configurations (in accord with E = mc²), although this binding energy cannot at all be associated with a particle of fixed size and density as required by a Lesagean interpretation. We could also mention the demonstrated deflection of light by gravitational fields, an effect which can hardly be reconciled with a Lesagean model. Neo-Lesageans typically appeal vaguely to some kind of refractive effect of the medium to account for this, but of course refraction tends to deflect light rays toward regions of higher density, whereas the density of Lesage’s ultra-mundane particles is actually lower near massive objects.

From a methodological standpoint it’s worth reflecting on the nature of the series of rationalizations that have been required in the efforts to maintain the viability of this model. The basic model consists of a flow of unseen particles in all directions tending to push the seen particles together, but this model tends to suggest many things (e.g., drag, saturation, aberration, heat transfer, temporal decay, mass accretion, dependence on volume, etc.) that are contrary to observation, so we have found it necessary to make extreme and convoluted assumptions about both the unseen and the seen particles in order to nullify the unwanted tendencies of the model. In fact, almost every inherent attribute of this model is inconsistent with the facts of gravity, and therefore must be minimized or nullified by setting some parameter of the model to near infinity or near zero. The positing of these unseen particles has taught us nothing new about gravity. Instead, we are using our pre-existing knowledge of gravity to infer things about the posited unseen particles as well as about the constitution of ordinary matter. Even if we overlook the fact that many of the implications are incompatible with our current best models of elementary particles (not to mention the fact that even if the model was correct it would not eliminate the need for an elementary force of attraction), we still would have to question the value of hypothesizing an occult entity (ultra-mundane particles) and then inferring the occult attributes of this occult entity necessary to yield the observed phenomena.

Incidentally, although Lesage’s model is merely a less sophisticated version of what had previously been proposed by Nicolas Fatio, such models are almost invariably referred to in modern literature as “Lesage theories” rather than “Fatio theories”. This is largely because Fatio’s writings were somewhat obscure, and have never been easy to acquire. Also, Lesage made no mention of Fatio (despite having collected his papers). As a result, most of those who discussed such theories in later years were unaware of Fatio’s priority. In fact, they may even have been unaware of Fatio’s existence, since he has always been considered something of an embarrassment to admirers of Newton. Nicholas Fatio was a promising (or at least plausible) young Swiss mathematician who first met Newton in 1689, and the two immediately began an intense relationship that ended abruptly in 1693 when Newton suffered a nervous breakdown. In the intervening years they often talked about sharing the same lodgings, and Fatio became so close to Newton that (according to Westfall) “Huygens and Leibniz came to regard Fatio as their intermediary through whom they learned about Newton’s opinions on mathematics, gravitation, and light”. Fatio was also in a position to cut off David Gregory’s access to Newton for a time.

Fatio’s admiration for Newton seems to have been boundless, and it was Fatio who initiated the charge that Leibniz had plagiarized the calculus from Newton. There was talk of Fatio editing the second edition of Principia, perhaps even including Fatio’s own contribution, i.e., his theory that gravity is produced by the push of tiny particles. Newton apparently humored him about this theory, and Fatio often proudly told people that Newton “did not scruple to say that there is but one possible mechanical cause of gravity, to wit that which I had found out”. Of course, this carefully worded statement is not exactly an endorsement (the word “possible” meaning not yet ruled out), and Fatio was honest enough to add “Tho he [Newton] would often seem to incline to think that gravity had its foundation only in the arbitrary will of God”. After the breakup with Newton, Fatio dropped out of sight, and later became devoted to a strange religious cult, the remnants of the Camisards, who preached that the end of the world was imminent, and whose leaders spoke in tongues and claimed to be able to raise the dead. (For more on this, see Fatio, Lesgae, and the Camisards.) Ironically, Fatio’s interest in prophetic sects was originally encouraged by Newton, but the latter was far more cautious in the public display of his heretical beliefs. At one point during their relationship Newton had written to Fatio

I am glad you have taken ye prophesies into consideration & believe there is much in what you say about them, but I fear you indulge too much in fancy in some things.

Return to MathPages Main Menu