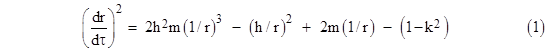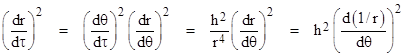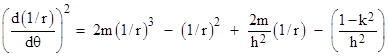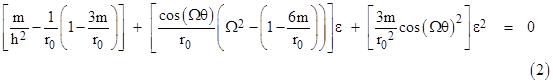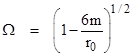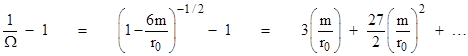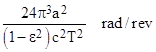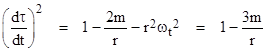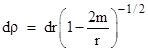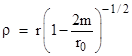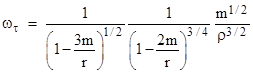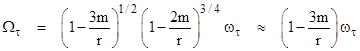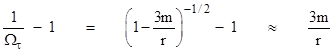On Relativistic Precession

The note on Anomalous Precession described how, from the Schwarzschild solution for a spherically symmetrical gravitational field, we can derive the equation of motion for a small orbiting test particle

where m is the mass of the central gravitating body in geometrical units, and h and k are constants of motion. Making use of the relation dθ/dτ = h/r², the left hand side of this equation can be written as

Thus we can write equation (1) in the form

Differentiating with respect to θ and dividing through by 2d(1/r)/dθ, we get

If r is constant, the left side vanishes and the right side gives the analog of Kepler’s third law. On the other hand, given a small periodic radial disturbance, this equation allows us to determine the period of that disturbance. Let 1/r = (1/r₀)(1 + ε cos(Ωθ)) for some small value of ε, where 1/r₀ is the mean reciprocal radius of the orbit, and Ω is the frequency at which a small radial disturbance propagates around the orbit. Substituting this expression for 1/r into the above equation, evaluating the second derivative, and collecting terms by powers of ε, we get

If the amplitude ε of the radial disturbance is zero, the second two terms vanish, and the first term corresponds to Kepler’s third law. On the other hand, for non-zero radial excursions we must choose Ω so that the second and third terms vanish. For sufficiently small ε the third term can be made arbitrarily small, so the vanishing of the second term represents the condition for infinitesimal radial disturbances. Thus an infinitesimal disturbance propagates around the orbit with the angular “frequency” given by

The orbital equation is

which would be a Keplerian ellipse if Ω were equal to unity, meaning that the radial disturbance has the same period as the angular position. One radian of the radial cycle takes place over 1/Ω radians of the angular cycle, so the precession of the radial cycle relative to the angular cycle is

Hence to the first order the precession is simply 3m/r₀. For example, the orbit of the planet Mercury has a harmonic mean radius of r₀ = (55.44)10⁶ km, and the mass of the Sun in geometrical units is m = 1.475 km, so a small radial cycle will precess relative to the angular cycle by (2.66)10⁻⁸ radians per radian, or equivalently revolutions per revolution. Multiplying this by (360)(60)(60) gives 0.1034 arc seconds per revolution. Since Mercury completes 414.9378 revolutions per century, we get the familiar result 42.92 arc seconds per century.

It might be objected that the eccentricity of Mercury’s orbit (ε = 0.206) is rather large, whereas our derivation stipulated arbitrarily small values of ε to ensure that the third term in the previous equation to be negligible. However, the third term is also negligibly small, for any value of ε, if the ratio of m/r₀ is sufficiently small, because this is the ratio of the coefficients of the second and third terms.  For astronomical orbits in our solar system this ratio is always quite small, so the above solution is valid for any eccentricity in these conditions.

Nevertheless, it’s worth bearing in mind that in general (i.e., for arbitrary values of m/r₀) the solution is valid only if the eccentricity is small. This requirement is somewhat obscured in many presentations, especially since they typically express the result in the form

where a is the semi-major axis of the orbit.  Of course, this is equivalent to 3m/r₀ with units of radians per radian, where r₀ is the harmonic mean radius of the orbit. The simpler form emphasizes the fact that the eccentricity doesn’t really enter into the result in a meaningful way. It appears in the traditional form only because of the choice to express the result in terms of the semi-major axis, and in order to relate this to the harmonic mean radius it is necessary to specify the eccentricity. But all that matters is the mean radius, and for any given mean radius there can be infinitely many different eccentricities (with their corresponding semi-major axes). As explained above, the solution is generally valid only for orbits with sufficiently small eccentricities, for which the value of the eccentricity drops out of the result.

The is analogous to the speed of propagation of a pressure wave in air. We find that for sufficiently small amplitudes the speed of sound in a given medium is essentially independent of the amplitude of the wave. Likewise for sufficiently small radial waves, the speed of propagation around an orbit is independent of the amplitude, i.e., the eccentricity. The traditional formula is misleading because it suggests that the physical effect of eccentricity has been taken into account in the solution, when in fact it has not. The value of ε appearing in the traditional formula merely serves to convert the semi-major axis (which is not a suitable parameter) to the harmonic mean radius. The physical solution is strictly valid only for essentially circular orbits with just infinitesimal radial perturbations. The only reason the formula is accurate for typical astronomical orbits with high eccentricity (e.g., the asteroid Icarus) is that m/r₀ is extremely small for these orbits. If we needed to determine the precession for an orbit with large eccentricity and a large value of m/r₀ (i.e., in an extremely strong gravitational field) we would need a more complicated solution, taking into account the third term in equation (2).

People sometimes wonder about the meaning of precession for a perfectly circular orbit, i.e., when the eccentricity ε is precisely zero. We should first point out that this question is not unique to relativistic precession, because the precession resulting from third bodies or non-spherical bodies in classical orbital mechanics also leads to values of precession that are independent of the eccentricity for nearly circular orbits, and hence that seemingly apply to perfectly circular orbits. In general there are several possible meanings of actual precession in a circle, such as precession of a cyclic variation in speed, or even in the position of the orbiting body, just as the faster of two runners on a circular track precesses in comparison with the slower runner. In the latter case, the precession simply implies that the body is moving slightly faster than it would have been moving in the absence of the precession, so we would expect to find the orbiting body progressively further and further ahead of its expected position based on the Keplerian two-body relation between speed and orbital radius. However, in neither the classical nor the relativistic cases can we make a direct comparison with the simple Keplerian two-body relation, because that relation assumes a single, perfectly spherical, gravitating body (which is not applicable to the conditions for classical precession), and it makes no distinction between coordinate and proper spacetime intervals (which makes it inapplicable to relativistic precession). In both cases the meanings of the parameters appearing in Kepler’s law become ambiguous, so it isn’t possible to single out any particular aspect of the orbit as the effect of precession.

The most useful way of interpreting precession for circular orbits is that, just as the speed of sound has a definite value even when there are no sound waves present, so too the speed of propagation of small radial disturbances around an orbit has a definite value even if there are no radial disturbances present. Of course, if ε is precisely zero, the second and third terms vanish identically, so no constraint is placed on Ω, but for any small non-zero ε, the value of Ω is determined. In other common derivations of the precession (such as Einstein’s original derivation, reproduced closely in Weinberg’s 1972 text) the difference between the maximum and minimum radial distance appears in the denominator of several expressions, so it is strictly undefined when the radial distance is precisely constant. Nevertheless, the precession approaches a constant value in the limit as the radial perturbation goes to zero, just as the speed of sound approaches a constant value in the limit as the amplitude of the pressure disturbance goes to zero. Needless to say, there is nothing paradoxical about this.

This explanation suggests that it might be possible to express the angular speed Ω of infinitesimal radial disturbances directly in terms of the differences between coordinate and proper intervals (analogous to expressions for the speed of sound in terms of the ratio of the differentials of pressure and density). We recall that the relativistic form of Kepler’s third law for circular orbits is

where ω_t = dθ/dt, and this can be expressed in terms of the proper angular speed ω_τ = dθ/dτ by multiplying by the square of dt/dτ along the orbital path. We can infer this ratio directly from the Schwarzschild metric (with dr = 0) in the plane of the orbit

Dividing through by (dt)² and noting that dθ/dt = ω_t, we get

Hence the coordinate angular speed is related to the proper angular speed by

Of course, this doesn’t signify a change in the speed of the orbiting body as seen from a distant observer, it merely expresses the fact that, in terms of a clock co-moving with the orbiting body, the angular speed has a slightly greater value than it does when evaluated in terms of a distant clock. Thus equation (3) can be written equivalently as

Now, we must also recognize that the radial Schwarzschild parameter r appearing in these equations cannot be strictly identified with the classical radial distance parameter. The Schwarzschild r is defined such that the area of the spatial surface at constant r is 4πr², but the spatial manifold is not flat, so this r is not the integrated proper spatial distance to the origin. In order to express the relativistic analog of Kepler’s third law entirely in terms of proper space and time variables for a circular orbit, we need to somehow convert the coordinate distance r to a “proper distance”. We might define the proper radial parameter as the integral of the proper spatial distance to the origin on a surface of constant time, but this is complicated by the fact that the Schwarzschild time foliation becomes singular at r = 2m. On the other hand, it can be argued, since we are interested only in infinitesimal radial disturbances, the relevant proper radial space parameter for a circular orbit ought to be in the same proportion to r as the differentials. At any given radial position, the differentials of the proper and the coordinate distances are related by the gravitational “boost” factor

For any given circular orbit with coordinate radius r₀, we can simply define a “proper” radial coordinate ρ related to the Schwarzschild coordinate r by

Thus when r = r₀ the differentials agree with the proper spatial measures. Now, beginning from the relativistic analog of Kepler’s law in terms of Schwarzschild coordinates

we substitute the proper parameters τ and ρ for the coordinate parameters t and r to give the equivalent expression

The quantity on the left side is simply the angular speed of a circular orbit in terms of a co-moving clock, whereas the rightmost factor on the right side looks like an angular speed of a classical circular orbit of radius ρ. What might this angular speed represent? Notice that, to the first order, each of the leading factors exceeds unity by (3/2)m/r, so the temporal and the spatial factors each contribute half of the relativistic precession, giving a total of 3m/r. Hence we are led to identify  the rightmost factor with Ω, the angular speed of the radial perturbation in terms of the proper time. Thus we re-write the above equation as

Just as before, we can now express the precession of the radial disturbance as

The pseudo-derivation hinges on the identification of the frequency Ω_τ of the radial disturbance with the quantity m^1/2/ρ^3/2, which admittedly is not terribly well motivated, but it does at least suggest an alternate way of conceiving of the frequency of the propagating radial cycle in relativistic orbits. In other words, it suggests splitting the relativistic “Kepler’s law” into two parts, one for the angular cycle, and one for the radial cycle. The latter can be expressed as

In the Newtonian two-body problem, a single frequency applies to both the angular cycle and the radial cycle, whereas in general relativity these are two different frequencies, so we need this second version of “Kepler’s third law”, to go along with the better-known angular version

If t = τ and r = ρ (as in Newtonian mechanics), these two are identical, but in general relativity they differ slightly, resulting in the relativistic orbital precession.

Return to MathPages Main Menu