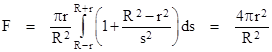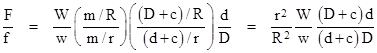Newton's Proposition LXXI

Newton's earliest speculations (in the 1660's) about universal gravitation involved a rough comparison between the acceleration of a falling apple near the Earth's surface and the acceleration required to keep the Moon in its orbit. He found the accelerations to be "pretty near" inversely proportional to the squares of the distances from the Earth's center. This is an interesting observation, but it isn't clear whether this is consistent with the idea of gravity as an attractive force exerted by every particle of matter on every other particle of matter. At great distances it's quite plausible that the attraction between two spherical objects should be closely expressible in terms of the distances between their centers, but it's not intuitively obvious that the net force near the surface of a massive sphere should be inversely proportional to the square of the distance from the center of the sphere, as if all the mass of the sphere were located at its center. In fact, Newton told Halley in 1686 (while still at work on the Principia) that he had only succeeded the previous year in convincing himself that the "duplicate proportion" (i.e., the inverse-square force of gravity) was actually valid at every distance from a spherical mass, even down to the surface of the sphere. The seriousness of his doubts about the validity of this proposition (which some scholars have claimed was the cause of the 20-year delay between Newton's first thoughts on universal gravitation and the composition of Principia) can be judged from his remark to Halley that

There is so strong an objection against the accurateness of this proposition that without my demonstrations... it cannot be believed by a judicious philosopher to be any where near accurate.

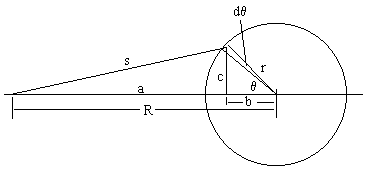
The problem can obviously be reduced to one involving just a thin spherical shell of matter, since we can build up a solid sphere from such shells. Interestingly it's fairly easy to see that the net force exerted by an inverse-square attraction to the individual particles of a shell on a point inside the shell is identically zero (see Inverse Square Forces and Orthogonal Polynomials), and this is suggestive of the unique correspondence between spherical distributions of matter and inverse-square force laws. When treated as a simple problem in integration the exterior points can be handled just as easily as the interior points. The usual approach is to consider a cross-section of a spherical shell as shown below:

By symmetry the forces perpendicular to the axis cancel out, so we need consider only the forces in the direction of the axis. The incremental force exerted by the ring of matter in the region dθ, when rotated about the horizontal axis, is

We also have

and we can take the differentials of both sides to give

Solving this for dθ and substituting back into (1), along with the expression for cos(θ) from (2), gives

Integrating this from s = R–r to R+r gives

For an interior point the same expression applies, except that the limits of integration are r–R to r+R, in which case the integral vanishes and we have F = 0.

Since Newton was in possession of his own version of calculus at this time, we might expect to find something like this integration in the Principia, but in fact Newton composed the Principia entirely without the (explicit) use of his method of "fluents and fluxions". This is usually attributed to his preference for the synthetic methods of the ancients, such as Archimedes, Euclid, and so on, but it's sometimes suggested that although the Principia contains no explicit calculus (setting aside the material the Newton added in later editions when trying to solidify his priority of invention), it nevertheless is based on the thought processes of calculus, merely disguised. It's certainly true that Newton made use of reasoning about "ultimate ratios", etc., but such reasoning has been employed since ancient times, notably by Archimedes. What distinguishes the modern calculus is precisely the formalized algorithms and systematic procedures for dealing with continuous functions (with or without a rigorous foundation), and these are almost entirely absent from the Principia.

To illustrate this point, let's consider how Newton actually proved his Proposition 71 concerning the net attraction of a spherical distribution of matter on an external particle. First we note that in Proposition 70 he treated the case of interior points simply by matching the opposite regions on the sphere and showing that they cancel, but this doesn't apply directly to the case of an exterior point. So, to finally settle his doubts about the attraction of spherical bodies, in 1685 he developed a synthetic demonstration by comparing the forces applied by a spherical shell on two external points at different distances, and showed that the forces are inversely proportional to the squares of their distances from the center of the sphere.

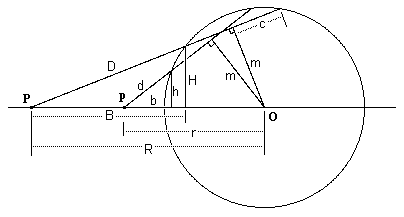
Consider a cross-section of a spherical shell of matter, and two external particles at P and p, as shown below.

Newton draws lines from P and p through the sphere such that they cut off equal arcs, which implies that both lines are an equal distance, denoted by m, from the center of the sphere. In terms of the distances indicated on this drawing, we know that the forces along the horizontal axis exerted on these two particles by the ring-shaped slices of the spheres (on the near side) swept out by rotating about the axis are

where W and w are the incremental widths of the rings. Hence the ratio of these forces is

Also we know the triangle with edges H, B, D is similar to the triangle with edges m, D+c, R, and likewise the triangle with edges h, b, d is similar to the triangle with edges m, d+c, r. Therefore B/D = (D+c)/R and b/d = (d+c)/r. In addition, H/D = m/R and h/d = m/r. Making these substitutions, we have

Now imagine the line through p rotating in the plane and sweeping over the entire circle to the point of tangency, and likewise the line through P can rotate and sweep over the entire circle to its point of tangency. The key idea is that we correlate the rotation rates of these two lines such that they are always at equal distance (denoted by m) from the center of the sphere. Hence, a very small rotation of the line through p results in a certain change in m, and this implies a corresponding rotation of the line through P. Hence these lines sweep through equal arc lengths at the radii d+c and D+c, which implies that the arc lengths they sweep out at radii d and D respectively are in the ratio d/(d+c) to D/(D+c). Also, since these lines always make the same angle relative to the surface of the circle, we know that the widths of the swept rings on the sphere are in this same proportion, i.e.,

Substituting this into the preceding expression gives the ratio of the forces

It's easy to show that essentially the same analysis applies to the rings on the opposite side of the tangency point. Hence Newton was finally able to prove to himself (twenty years after the question first occurred to him) that, in fact, the force exerted by a spherical mass on any external particle varies inversely as the square of the distance of that particle from the center of the sphere, and this remains exactly true all the way down to the surface of the sphere. This created a logically coherent foundation for the theory of universal gravitation.

It's hard not to admire the ingenuity that Newton displayed here and throughout the Principia, producing time after time a clever synthetic demonstration of a fact that would (today) be treated by calculus. On the other hand, it's interesting that although Newton was in possession of his fluents and fluxions since the mid 1660's, he never took the occasion to settle his question about the force of attraction of a sphere with an inverse-square law - at least not until 20 years later, and then he resolved the question by means of a synthetic demonstration, rather than by explicit use of fluents and fluxions. It has sometimes been suggested that Newton wrote two versions of the Principia, first using calculus, and then re-writing it in the synthetic style. However, in the case of Proposition 71, it seems to me that Newton's published method is not very suggestive of the way this problem would be approached using calculus. The whole strategy of taking the ratios of the forces on two distinct points, and of splitting up the demonstration into two parts for internal and external points, seems (to me) to imply that this synthetic demonstration was the one that Newton referred to in his comment to Halley, i.e., this is the thought process by which he (after 20 years) arrived at this conclusion. Despite being one of the inventors of modern analysis, the classical synthetic mode of thought seems to have been more to his liking.

Return to MathPages Main Menu