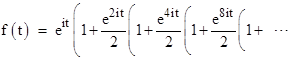|
Ptolemy's Orbit |
|
|
|
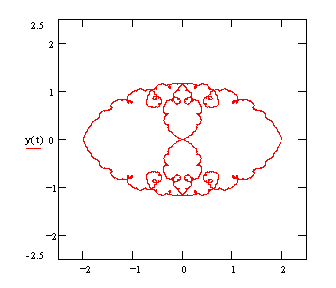
Ptolemy constructed planetary orbits from compound circular motions. Consider a point p1 moving in a circular path of radius R at a constant speed of 1 rad/sec around a point O. A second point, p2, revolves around p1 at a radius of R/2 and a speed of 2 rad/sec (relative to a frame of reference rigidly connected to p1). Continuing to add epicycles in this way, each with half the radius and twice the angular velocity of the preceding one, we arrive at an interesting fractal orbit, which can be expressed in complex form as |
|
|
|
|
|
|
|
A plot of this orbit is shown below: |
|
|
|
|
|
|
|
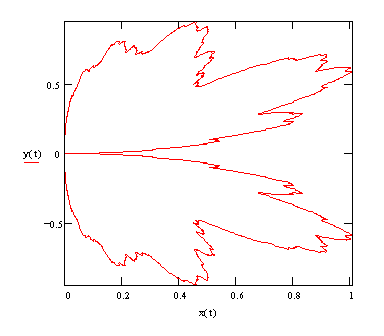
Another interesting object, that might be called "Ptolemy's Leaf" (because of it's resemblance to an oak leaf), is formed by plotting Re(f(t))cos(t) vs Re(f(t))sin(t). This is illustrated in the plot below: |
|
|
|
|
|
|
|
A somewhat similar construction begins with an arbitrary triangle with edge lengths 1,a,b where a and b are both less than 1. Then we construct similar triangles on each of the legs, and then similar triangles on each of those legs, and so on. To illustrate, here is a picture based on a triangle with sides proportional to 1, a = 0.4, b = 0.77629... |
|
|
|
|
|
|
|
This shows the intermediate stages as it approaches the ultimate fractally looping curve. The perimeter length of the original ramp is just a+b, and the next stage has segments of length a2, ab, ab, and b2, so it's length is (a+b)2. And so on. Obviously at the nth stage the path contains exactly C(n,k) segments of length an−k bk, and the total length is (a+b)n, going to infinity as n increases, and the path approaches the true fractal curve with loops on all scales. This is quite similar to Koch's "snowflake" construction. |
|
|