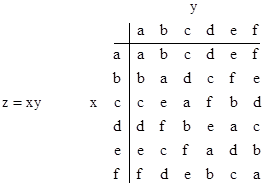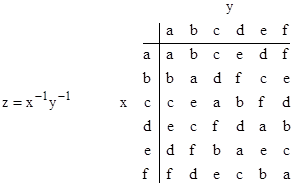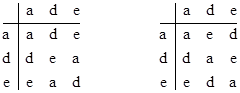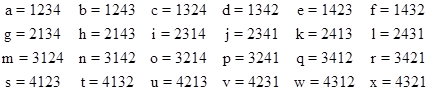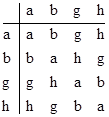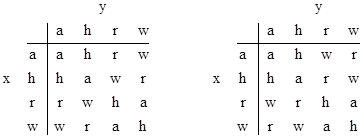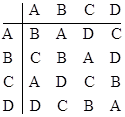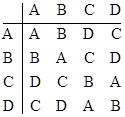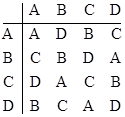Quasi-Groups

A mathematical group is a set of elements with an associative operation that maps any two elements (not necessarily distinct) of the set to an element of the set, and such that there is a unique identity element and each element has a unique inverse. We will denote the operation by juxtaposing elements. For example, if x and y are two elements then xy is also an element. Any group can be represented by a set of permutations together with the operation of “composition”, meaning that we apply first one permutation and then the other.

Any given group has a “multiplication table” giving the result of operating on any two elements. For example, consider the set of all possible permutations of three items. The elements of this set are

The "multiplication table" for these six elements under compositions is shown below:

By convention we denote by xy the operation of applying permutation y first, followed by x. This may seem lexicographically backwards, but it is intended to convey that these permutations operate on a string S of distinct characters, so successive operations on S would be written as x(y(S)). The table shows that (for example) db = f, which signifies that applying the permutation b followed by the permutation d is the same as applying the single permutation f. To confirm this, note that b simply transposes the second and third characters, so the string 123 becomes 132, and then d moves the second character to the first position, the third character to the second position, and the first character to the third position, so the string 132 becomes 321, which is simply f.

Clearly the element “a” is the identity element of this group, and, as required, the group operation is associative, meaning that for any three elements x, y, and z we have (xy)z = x(yz). The group operation is not commutative, however, as shown by the fact that db = f and bd = c.

Now suppose we consider a different structure, consisting of the same group elements, but instead of using ordinary composition xy to create the multiplication table, we use x*y = x⁻¹y⁻¹. In other words, the operation for two elements consists of composition of the inverses of those elements. Since each element is it’s own inverse except d⁻¹ = e and e⁻¹ = d, it follows that the multiplication table with this operation is given by swapping the rows and columns of d and e, as shown below.

This is not a group, because there is no unique identity element, as shown by the fact that ad = e. Also, this operation is not associative, since we have e(bc) = a, whereas (eb)c = e. However, this table does have some aspects of a group, namely, closure and unique inverses. In other words, if x and y are in the set, then x*y and y*x are also in the set, and each elements appears exactly once in each row and each column of the multiplication table. We will refer to such a structure as a quasi-group.

By the way, we might also consider the operation z⁻¹ = x⁻¹y⁻¹, which would have the effect of simply transposing d and e in the above table. However, this operation is obviously equivalent to z = (x⁻¹y⁻¹)⁻¹ = yx, so the multiplication table would simply be the transpose of the original group table.

The original group and the quasi-group each have a sub-group (or sub-quasi-group) of 3 elements

as well as three isomorphic subgroups of 2 elements, {a,b}, {a,c}, and {a,f}.  As these examples confirm, every quasi-group generated by (2) has the property that xx=a for every x in the set, and of course any two of x,y,z uniquely determine the third (meaning that each element appears exactly once in each row and each column).

The twenty-four possible permutations four items are

The elements that are not their own inverses consist of the pairs de, im, js, kn, lt, pu, and rw. There are seven sub-groups of four elements. Four of these, namely {a,b,g,h}, {a,c,v,x}, {a,f,o,q}, and {a,h,q,x}, consist of self-inverse elements and have a multiplication table isomorphic to

regardless of whether we choose ordinary composition or the composition of inverses as the group operation. The remaining three are the sets {a,h,r,w}, {a,j,q,s}, {a,k,n,x}, each of which consists of the identity, one self-inverse element, and one pair of reciprocal elements. These represent either a group or a quasi-group, depending on whether ordinary composition or the composition of inverses is taken as the operation. Accordingly the resulting multiplications are isomorphic to one of the following:

Again, the multiplication table for the quasi-group (i.e., the right hand table) does not have a unique identity element and it is not associative, as shown by (ah)r = r and a(hr) = w.

If, instead of defining the multiplication table as the composition of the inverses of both elements, we defined it by inverting just one of the arguments, such as z = xy⁻¹, then we would just transpose the columns or the rows (but not both).

Another example of a quasi-group with four elements is shown below.

Is this quasi-group represented by a set of permutations, and, if so, what is the rule of composition that generates this table? Can every quasi-group be represented by a set of permutations with some "composition" rule? Granted, we can always imagine an "ad hoc" composition rule that generates any given quasi-group when applied to any given set of objects, but is there a "canonical form" of composition rule that will generate all quasi-groups? For example, if we define the operation z=x*y using the formula zxy = I then the set of permutations {A=1234, B=2143, C=3421, D=4312} yields the quasi-group

whereas the set {A=1342, B=2431, C=3124, D=4213} gives the quasi-group

This illustrates how a single rule of composition can yield distinct quasi-groups depending on the choice of elements of S₄ to which it is applied.  The latter quasi-group can also be generated using the rule z = yxyx on the same four elements of S₄, so for that particular quasi-group we have a choice of definitions for the “multiplication” rule. Can every quasi-group can be generated by an operation of this type applied to an appropriate set of permutations?

Return to MathPages Main Menu