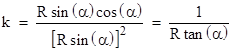Did Archimedes Know Gauss-Bonnet?

One of the most beautiful propositions of mathematics is called the Gauss-Bonnet formula, which states that the integral of the Gaussian curvature over a region of a surface equals 2π minus the integral of the geodesic curvature over the boundary of that region. This was first stated and proved by Bonnet in 1848. The name of Gauss is attached to the formula because Gauss published the special case for geodesic triangles, i.e., triangles whose sides are geodesics of the surface.

If we further specialize to a spherical surface, Gauss' result was actually proved by Thomas Harriot in 1603. Given a spherical triangle with angles α, β, γ, Harriot's proof was based on the fact that any two edges of the triangle, when extended, constitute two great circles that intersect at opposite poles, and the surface area between two such "longitude lines" is simply 2αr² where r is the radius of the sphere and "a" is the angle between the longitude lines, i.e., one of the angles of the original triangle. So, letting A denote the area of the spherical triangle, and letting A_α, A_β, A_γ the areas of the three longitude slices less A, we have

Consequently

Noting that

because this covers the entire sphere, we can eliminate the sum in parentheses on the left side to give the result

The Gaussian curvature of the sphere's surface is a constant 1/r², so the left side is the integral of the curvature over the surface of the triangle, which equals the "angular excess", i.e., the amount by which the sum of the three angles of the spherical triangle exceeds π.

Now, if we're willing to interpret early results in such a charitable way, we might just as well make the case that Archimedes proved a special case of the Gauss-Bonnet formula. As discussed in Archimedes on Spheres and Cylinders, Archimedes proved that the surface area of a region of a sphere of radius R sliced off by a plane equals the area of a circle whose radius is the straight-line distance from the central point of that region to the perimeter. If we project the slice locus onto a plane tangent to the sphere at any point of the slice, it forms an ellipse with major and minor radii Rsin(α) and Rsin(α)cos(α) respectively. Hence the geodesic curvature of this boundary is

The circumference of that locus is 2πR sin(α), so the integral of the geodesic curvature around this locus is

Archimedes proved that the surface area bounded by this locus equals

The Gaussian curvature of the sphere is a constant 1/R², so the integral of the curvature throughout the enclosed area is

Thus we can express Archimedes' result in the form

which is the celebrated Gauss-Bonnet formula. Admittedly Archimedes was restricted to spherical surfaces, but unlike Harriot or Gauss his perimeter was not a geodesic.

Return to MathPages Main Menu