Loci of Equi-angular Points

Given a line segment AB, the loci of points P such that the angle APB has a constant value are circular arcs that pass through the points A and B. As a special case of this we have the well-known fact that if APB is a right angle, then the locus of points is the circle with the diameter AB. In general, if AB is any chord of a circle, the angle APB for any point P on the circle is constant except at the singular points A and B themselves. (Note that if the chord is not a diameter of the circle, the constant angle will be different on either side of the chord.)

This is equivalent to the fact that for any three points A, B, and C on a circle, the angle ABC depends only on the distance from A to C. Of course, if O is the center of the circle, it follows that the angle AOC depends only on the angle ABC (and vice versa). Another interesting equivalent statement is: If a particle travels in a circular path at constant speed, then its angular velocity about any fixed point on the circle is constant.

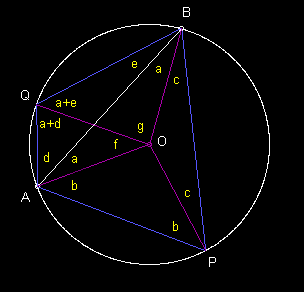
For a simple proof of the equi-angular property of circles and chords, consider the figure below.

We've labeled the angles taking advantage of the fact that the triangles with one vertex at the central point O and the other two vertices on the circle are isosceles. Since the sum of the interior angles of a triangle is π, we see immediately from the triangle ABP that

and therefore

which is constant for every point P. Strictly speaking we've only shown this when ABP contains the point O, but it's not hard to show that it also applies even if O is outside ABP, as long as P is on the larger of the two arcs of the circle cut by the segment AB.

On the other hand, for point such as Q, on the smaller of the two arcs cut by AB, we can examine the triangles OAQ and OBQ to give the relations

Adding these gives

Also, from the triangle AOB we have 2a + (f+g) = π, so we can substitute for (f+g) into the preceding equation to give

which again is constant for all points Q on the smaller arc. Notice that the line tangent to the circle at A makes an angle of π/2 with the line OA, and so it makes the angles π/2 + a and π/2 - a with the line AB. This stands to reason, because the lines AP and AQ approach this tangent line (from opposite sides) as P and Q approach A.

A trigonometric proof of this equi-angular property in the xy plane goes like this: Let T denote the point (0,1) at the top of a unit circle, and let P denote another point on the circle with coordinates (x,y). If 'a' is the clockwise angle between the horizontal and the line TP, then the equation of the line is simply

Inserting this into the circle's equation x² + y² = 1 and solving for x gives

and so y = cos(2a). This shows that the angular velocity about the point T is always exactly 1/2 the angular velocity about the center of the circle. Thus, when P sweeps out a given angle about the point T, it sweeps out exactly twice that angle about the center, regardless of where on the circle point P happens to be relative to T. This proves that the length of the chord is fixed for a given swept angle about T.

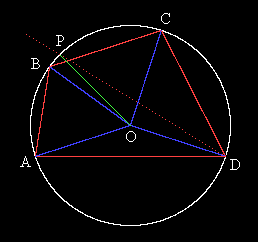
One immediate consequence of this is the fact that if a quadrilateral is inscribed in a circle, and we construct the bisectors of the angles at the vertices, the intersections of these bisector lines with the circle form a rectangle. This is illustrated for the quadrilateral shown in red inscribed in the circle below.

The dotted red lines bisect the interior angles of the quadrilateral, and the points where these lines meet the circle comprise the vertices of the green rectangle. To prove that it is, in fact, a rectangle, consider the figure below.

The blue lines are radii from the center O of the circle to the vertices of the original quadrilateral. Now, as the red dotted line through vertex D rotates at constant angular speed from the line DA to the line DC, the green line OP from the center of the circle to the point of intersection of the red dotted line with the circle rotates at twice the angular speed. Hence the line DP bisects the angle ADC precisely when the radii OP bisects the angle AOC. Likewise the bisector of the interior angle ABC strikes the circle at the same points as does a radii from the center bisecting the angles AOC on the in the other direction. Similarly the other two points of interest fall along the radii from the center that bisect the angle BOD in both directions. Hence each diagonal of the resulting figure is a diameter of the circle, so the figure is a rectangle.

Return to MathPages Main Menu