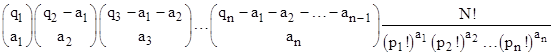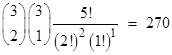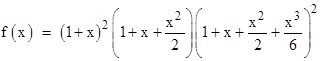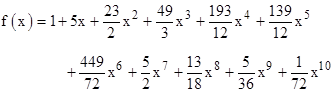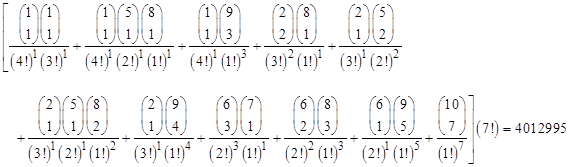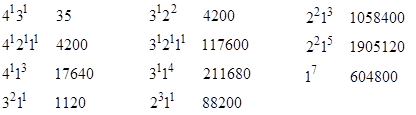The Statistics of Counterintelligence

The conversation of prayers about to be said

By the child going to bed and the man on the stairs

Who climbs to his dying love in her high room...

                                                        Dylan Thomas

How many different 5 letter 'words' can be constructed from the letters of the word 'statistics'? (In this context a "word" isn't necessarily an English word. It merely signifies a string of five letters.) To answer this question, note that the word 'statistics' defines the partition [3,3,2,1,1] of 10. Each 5-letter word must be a sub-partition of this, meaning that 5 is split into a sum of five non-negative parts, each no greater than the corresponding element of the given partition of 10. These sub-partitions contribute the following numbers of distinct words:

      [3,2]:    {2,1} {2,1} {5,2}     =    40

    [3,1,1]:    {2,1} {4,2}  5!/3!    =   240

    [2,2,1]:    {3,2} {3,1} (5) {4,2} =   270

  [2,1,1,1]:    {3,1} {4,3}  5!/2!    =   720

[1,1,1,1,1]:          {5,0}   5!      =   120

                                         -----

                          total       =  1390

where {m,n} signifies the binomial coefficient "m choose n". To explain these values, let's focus on the 5-letter words that correspond to the target partition [3,2], meaning that the words consist of 3 copies of one letter and 2 copies of another letter. To construct a word of this type (from the letters of the source partition [3,3,2,1,1], consisting of 3 s, 3 t, 2 i, 1 a, and 1 c letters) we would first select the letter that will have three copies, so it must be either "s" or "t". This requires us to choose one of two items, and the number of ways of doing this is {2,1} = 2. Then we must select the letter that will have two copies, and this must be either "i" or else one of the letters s or t, whichever one we didn't select in the first step. So again we must select one of two possible choices, and there are {2,1} ways of doing this. So, the total number of ways of populating the [3,2] partition is the product {2,1}{2,1} = 4, consisting of the four possible sets (s,t), (s,i), (t,s), and (t,i). Then, for each of these four distinct pairs of letters, with three copies of the first and two copies of the second, we can arrange them in {5,2} = 10 distinct ways, so the total number of words with the [3,2] partition is {2,1}{2,1}{5,2} = 40.

To formalize this, let’s write each target partition in the form [p₁^a1, p₂^a2,...p_n^an] where p_j denotes a valency and a_j denotes the multiplicity. For example, instead of writing [2,2,1] we will write [2²,1¹], and instead of writing [2,1,1,1] we will write [2¹,1³]. Also, for each p_j let q_j denote the number of elements of the source partition greater than or equal to p_j. In these terms we can express the number of distinct N-letter words for given source and target partitions as

For example, with the target partition [2²,1¹] we have p₁=2, a₁=2, q₁=3, and p₂=1, a₂=1, q₂=5. Inserting these values into the above expression gives

There's also a generating function for this type of problem, where the order of the elements is important. It's called an exponential generating function. For example, the number of 5-letter words that can be formed from 'statistics' is the coefficient of x⁵/5! in the function f(x) defined by the product of

The first squared factor corresponds to the fact that two of the letters ('a' and 'c') can have either 0 or 1 appearance. The middle factor signifies that one of the letters ('i') can have 0,1, or 2 appearances. The squared right-hand factor represents the fact that two of the letters can have 0, 1, 2, or 3 appearances. Expanding this out gives

so the coefficient of x⁵/5! is (139/12)(5!) = 1390. By the same method we can compute that there are 61751760 nine-letter words that can be formed from the letters of 'transubstantiation', and there are 4012995 seven-letter than can be made from the letters of 'counterintelligence'. The latter result is given explicitly by the permutation method described previously as

Clearly the partition method is simply a way of directly computing the coefficient of the relevant term of the applicable generating function, without having to expand the entire function. Notice that although there are 15 partitions of 7, only 11 of them contribute to this sum because the other four involve multiplicities of 5, 6, or 7, which are not possible in this example since the highest multiplicity of the source partition (for ‘counterintelligence’) is 4. The numbers of words for each of these partitions are

Thus almost half of the approximately four million 7-character words that can be formed from the letters of ‘counterintelligence’ are of the partition 2²1⁵.

Return to MathPages Main Menu