The Bulging Earth

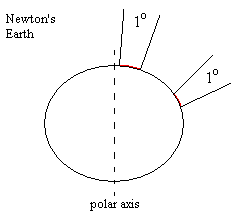
According to Newtonian mechanics the spinning of a planet on its axis should cause it to bulge at the equator. This is the content of Proposition 18 of Book III of the Principia, and in Proposition 19 Newton estimates that the equatorial diameter of the Earth differs from the polar diameter by about 1 part in 230. (Modern estimates are about 1 part in 297.4.) One of the confirmations of Newton's theory was provided by the astronomer Giovanni Domenico Cassini, director of the Paris observatory, who determined by direct observation that the planet Jupiter is (as Newton’s theory predicts) wider at its equator than from pole to pole. Another method of testing Newton’s claim would be to determine how many miles, in the North-South direction, correspond to one degree of latitude at the equator and as the poles. If Newton was correct, the distance corresponding to one degree of latitude should be shorter at the equator than at the poles, as illustrated in the figure below.

Notice that the word “latitude” is taken to signify the angle of the line perpendicular to the surface. According to Newton’s theory, if we regard the Earth as perfectly malleable, the surface would approach an equi-potential surface, taking both the gravitational and the centripetal acceleration into account, so that a plumb bob would point along this perpendicular line.

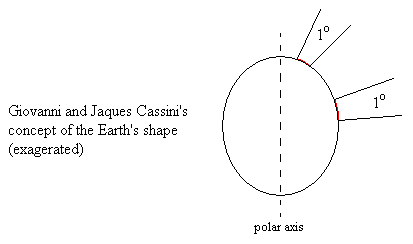
Ironically, Giovanni Cassini and his son Jacques disputed Newton’s concept of an equatorial bulge for the Earth. Their geodesy measurements – extending from Dunkerque in the North to Spain in the South – indicated that one degree of latitude was shorter near the poles than near the equator, as illustrated in the figure below.

Note that we are again taking the word “latitude” to signify the angle of the line perpendicular to the surface, despite the fact that in this context we cannot really identify this line with the direction of a plumb bob. We could make use of Newton’s laws to predict the local “plumb” direction at each point, but of course this would not in general be perpendicular to the surface. On the other hand, if we hypothesize this elongated shape for the Earth, we should also hypothesize laws of physics that would result in the Earth having this shape. These considerations are clearly significant, because if (for example) we suppose a plumb bob will always point toward the geometric center of the Earth, then one degree of latitude would cover a larger distance near the poles than near the equator. So the definition of latitude as the direction perpendicular to the surface is crucial to the Cassini prediction – despite the lack of any theory in which this direction coincides with the local plumb direction.

Incidentally, beginning with Giovanni Domenico Cassini (1625-1712), the position of Director of the Paris observatory was held by the Cassini family for four generations. Giovanni was succeeded by his son Jacques (1677-1756), who was succeeded by his son Cesar Francois (1714-1784), who was succeeded by his son Jacques Dominique (1748-1845). Each of these descendents of Giovanni were born at the Paris observatory, and their dates indicate hereditary longevity, living to the ages of 87, 79, 70, and 98 respectively.

The controversy over the Earth’s shape was finally "settled" by the expedition led by P.L.M de Maupertius in 1736, who went to Lapland to make measurements near the arctic circle. These measurements brilliantly confirmed Newton's theory, very much as Eddington's expedition to Africa to view the Solar eclipse in 1919 confirmed Einstein's theory... although it's interesting to note that in both cases it was later determined that the errors in measurements were so great that neither of these confirmations was really very solid. In the late 1920's Leinberg found that Maupertius' has accumulated errors - all in the same direction - so that his results strongly confirmed the equatorial bulge, but if he had accumulated these same errors in the opposite direction his results would have been totally inconclusive.

As an aside, this was neither the first nor the last time that a scientific issue has been "settled" by an experiment later shown to have been inconclusive – even though the conclusion was fortuitously correct. It's hard to avoid the impression that experimentalists are sometimes influenced by their expectations, i.e., by their pre-conceived beliefs about what answer must be correct. After all, how could the spinning Earth possibly not bulge at the equator? And Eddington was certainly convinced of general relativity prior to his eclipse expedition in 1919. In any case, Voltaire (an avid supporter of Newton) was inspired to composed a couplet making light of Maupertius and his far-flung measurements, roughly translated as

He confirmed with great effort at distant places

What Newton knew without ever leaving home.

Of course, it's one thing to predict that a spinning planet will bulge at the equator, and quite another to provide a quantitative estimate of the magnitude of this bulge. This is actually a somewhat tricky problem, because the Earth's actual shape is quite complicated (when considered in close detail), it's density is not uniform, and its gravitational field is not simple. To approach this difficult problem, Newton's basic idea was that the Earth must rise toward the equator by an amount that compensates very nearly for the increasing centripetal tendencies because, as Newton put it

...if our earth were not a little higher around the equator than at the poles, the seas would subside at the poles and, by ascending in the region of the equator, would flood everything there.

The implication is that the Earth's surface must be (very nearly) an equi-potential surface, because otherwise the waters would slide sideways in the direction of the lower potential. Of course, this compensation is not merely coincidental, because the entire Earth was once spinning in a molten state, so we would expect it to have solidified with an equatorial bulge. Admittedly the rotation rate of the Earth has been reduced since then, but the Earth is still malleable enough to respond (over millions of years) to the changing forces and maintain a roughly equi-potential surface.

From a relativistic standpoint, the natural paths of objects tend to veer in the direction of slower proper time, which is why particles fall in the direction of massive objects where the rate of proper time is lower. In effect, the total "potential" of an object in any state of motion and in any gravitational field can be defined as the derivative dτ/dt, where τ is the object's proper time and t is the time coordinate far from any gravitating bodies. Hence, the traditional cute answer to the question of whether ideal clocks run faster at the poles or at the equator is that they run at the same rate, almost by definition, because the surface of the Earth is an equi-potential (i.e., equi-time-rate) surface.

Unfortunately the cute answer is not entirely correct, for several reasons. First, the Earth's surface is not perfectly equi-potential, because it isn't perfectly malleable. Second, actual clocks respond differently to variations in gravitational vs centripetal acceleration. Even assuming an equi-potential surface, the effective weight of a given mass is less at the equator than at the poles (inversely proportional to the radii). Indeed one of the first confirmations of the equatorial bulge was the observation of the astronomer Jean Richer (1630-1696) that pendulum clocks run about 2.5 minutes slower per day at Cayenne in French Guiana (at the Northern end of South America) about 5 degrees North of the equator than at Paris, which is nearly 49 degrees North of the equator. Nevertheless, an ideal clock (one that does not rely on the local vertical weight of an object), such as a cesium clock, would run at the same rate at all points on an equi-potential surface.

On the other hand, we should be careful to specify just what we mean by "potential" in a relativistic context. In arbitrary spacetimes it can be tricky to define a meaningful potential, but of course when dealing with problems involving terrestrial phenomena we can model the Earth as an isolated body in an asymptotically flat spacetime, possessing a nice time global coordinate "t" (as in the Schwarzschild coordinates). In such a spacetime it is reasonable to define the potential at any given point of any given worldline is simply dτ/dt, which makes the relation between potential and "time dilation" tautological.

Having made this definition, we can show that a non-viscous rotating blob of matter (possessing some natural self-repulsion) in equilibrium will have a shape whose surface has constant dτ/dt. An arm-waving "proof" is just to point out that each part on the surface of the blob would slide tangentially if dτ/dt at any neighboring location was greater than at its current location, because it wants to maximize its dτ/dt (to get as close to a geodesic as it can, under the constraint of its repulsion from the surrounding material). This is essentially just a re-statement of Newton's argument about the distribution of the seas. It would be interesting to see a rigorous proof of the exact equi-potentialness of the surface, particularly at intermediate latitudes of an oblate spheroid, where the centripetal acceleration is not parallel to the gravitational acceleration". Since we don't have an exact solution of the field equations for an oblate spheroid, a rigorous proof would presumably have to be based on more fundamental considerations.

Assuming the equi-potential surface has constant proper time, we can begin by noting that a disproportionate fraction of the Earth's mass is located in its core, so we will not be too far wrong if we assume (at first) a spherically symmetrical gravitational field. In other words, assume that the shape (and rotation) of the Earth's outer mantle and surface doesn't have much effect on the field. For a particle with constant radial coordinate r and constant latitude q, the proper time τ is given by the line element

where ϕ is the longitude and t is the Schwarzschild time coordinate (which corresponds to the proper time of a sufficiently distant static observer). Dividing through by (dt)², setting ω = dp/dt, and using the expansion (1–x)^1/2  ~  1 – x/2 gives

At the North pole we have θ = 0 so this is just 1 – m/r where r is the distance from the North pole to the center of the Earth. At the equator we have θ = π/2, and distance to the center of the Earth is R = r + h, where h is the height above the Earth's nominally spherical surface representing our first approximation of the equatorial bulge. This gives dτ/dt = 1 – m/R – (1/2)R²ω². Subtracting the proper time rate at the pole from the proper time rate at the equator gives

The Earth's bulge is relatively slight, so the first-order effect dominates, and the break-even height h is approximately r⁴ω²/(2m). This is the height above the surface of a perfectly spherical Earth at the equator such that the rate of an ideal clock equals the rate of ideal clocks at the poles on the Earth's surface. The height for other latitudes θ can be computed from the previous expression.

However, if we fill up the envelope of equal-time-rate height h(θ) with matter having the same density as the Earth, the equatorial time rate will be slowed back down somewhat. This means we need to raise the elevation of the equatorial clock by an additional amount to make its rate equal the polar rate. Since the ring of equatorial matter produces, at a nearby point, only about half the gravitation of a complete spherical shell, and since the sensitivity of clock rate to height is roughly unchanged, we may assume that the additional increase in elevation is only about half the original elevation h. If we then fill up the region to h + h/2 we will again reduce the equatorial clock rate, so we will need to further increase the elevation by half as much again, and so on. This sequence of approximations leads to the convergent series for the total equatorial bulge

The mass of the Earth (in geometrical units) is m = 0.00443 meters, the angular speed of the Earth is w = (2.424)10^–13 rad/meter, and the nominal radius of the Earth is about r = (6.38)10⁶ meters, so we estimate that the Earth's equatorial radius exceeds its polar radius by approximately 22,000 meters. The compares remarkably well with the best modern measurements of the Earth's actual equatorial bulge, which give the currently accepted value of about 21,476 meters (which is 1 part in 297.0).

The formula should also be roughly applicable to the other planets. For example, the planet Jupiter has a radius 10.79 times the Earth's radius, it's mass is 318.1 times the Earth's mass, and it's rotational speed is 2.421 times the Earth's rotational speed. Therefore, using the expression b = r⁴ω²/m we would estimate that the difference between the polar and equatorial radii of Jupiter is about 250 times the difference for the Earth, which gives about 5.2 million meters. Current measurements of Jupiter indicate that the actual difference is 4.3 million meters, so our rough formula is about 20% high. This is probably attributable to the greater variation in density of Jupiter, whose outer layers are gaseous. As a result, the sequence of corrections may give a geometric factor of something like (1 + 1/3 + 1/9 + ...) = 3/2 instead of 2 as in the case of the Earth with its rocky mantle.

Denoting the constant "geometric factor" by k = 1/(1–f), we can express our basic equation for the bulge of a spinning planet in the form

where ρ = m/[(4/3)πr³] is the density. The factor f accounts for variations in density, and is about 1/2 for the Earth and slightly greater than 1/3 for Jupiter. This equation is consistent with Newton's statement that

If a planet is larger or smaller than the earth, while its density and periodic time of daily rotation remain the same, the ratio of centrifugal force to gravity will remain the same, and therefore the ratio of the diameter between the poles to the diameter at the equator will also remain the same. But if the daily motion is accelerated or retarded in any ratio, the centrifugal force will be increased or decreased in that same ratio squared, and therefore the [ratio of] the diameters will be increased or decreased nearly in the same squared ratio. And if the density of a planet is increased or decreased in any ratio, the gravity toward the planet will also be increased or decreased in the same ratio, and the difference between the diameters in turn will be decreased in the ratio of the increase in the gravity or will be increased in the ratio of the decrease in gravity.

By the way, to quantify the magnitude of the differences in time rates that result in these bulges, notice that if the Earth was perfectly spherical with radius r, then a clock at the equator located at an elevation of 21 kilometers would have a rate exceeding the rate at the pole by (1.074)10^–12 sec/sec, which gives about 92.8 extra nanoseconds per day. This is the net effect of +(2.278)10^–12 sec/sec due to high elevation and –(1.204)10^–12 sec/sec due to rotation.

It's also interesting that on the equator we have the general equation for any radius r

Differentiating this with respect to r gives

The first term on the right corresponds to the classical "acceleration of gravity" and the second term is the centripetal acceleration v²/r, so we see that the mixed second derivative d²τ/(dt dr) can be identified with the net "acceleration".

Return to MathPages Main Menu