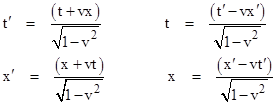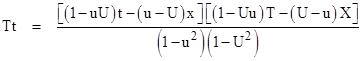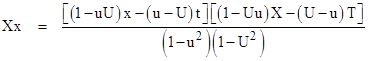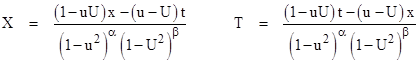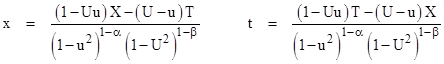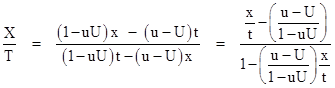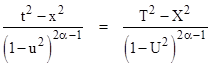General Transformations and Relative Rotation

If the relationship between inertial coordinate systems is given by the Lorentz transformation then the composition rule for (co-linear) speeds is

However, the converse is not true; the relativistic speed composition formula does not uniquely imply the Lorentz transformation. This composition formula is consistent with any of a larger class of transformations. The formula can be written in either of the two algebraically equivalent forms

Now consider an arbitrary event on the time axis of frame 3, and let x′,t′ denote the inertial coordinates of this event in terms of frame 1, and let x,t denote the inertial coordinates of the same event in terms of frame 2. Hence we have v₁₃ = x′/t′ and v₂₃ = x/t, and the mutual velocity between the x,t and x′,t′ coordinate systems is v = v₁₂. Inserting these values into the above equations, clearing the denominators, and dividing through by 1 – v² gives

The symmetrical factorizations

are the only one strictly consistent with the relativistic principle that the single parameter v fully characterizes the relative states of motion of two objects, but we can consider other possible factorizations while maintaining the relativistic speed composition rule. In general, for any of the non-symmetrical factorizations, the state of motion of each object is characterized by an absolute parameter.

For example, given two co-linearly moving particles p and P at rest in the inertial coordinate systems (x,t) and (X,T) respectively, we must specify two absolute speeds, denoted by u and U. The relativistic composition rule requires that equation (1) be satisfied, where the single relative speed v in that equation is replaced with the relativistic difference (u−U)/(1−uU). Making this substitution, we have the general relations

These expressions can be factored to give a generalized Lorentz transformation law. Since we now have individual speeds for the two frames of reference, it's not necessary to assume that the denominators factor as simple square roots. Let the exponents in the factored denominators be specified by two arbitrary parameters α,β, leading to the general transformation

and conversely

The invariance of lightlines in all frames can be seen by noting that if x = t for some point (x,t) on a ray emanating from the origin, then we have X = T. In general, straight lines map to straight lines. Also, by construction, the relativistic composition law remains valid for any values of α and β, which we can verify explicitly from the ratio

The quantity in parentheses in the right-hand expression is the relativistic speed between the two frames of reference, and the quantities x/t and X/T correspond to the speeds of a particular worldline though the origin to the point (x,t), and the above expression relates these speeds to the difference in the frame speeds in accord with the relativistic composition law.

This parameterization should not be confused with the usual one-parameter family of simultaneity conventions, each of which essentially represents a different assumption about the one-way speed of light as a function of absolute direction in space, and is operationally equivalent to the symmetrical Lorentz transformation. In contrast, the above two-parameter family doesn't prefer any particular spatial direction, nor is it operationally equivalent to the symmetrical Lorentz transformation, except with α = β = 1/2. The above transformations imply

Obviously if α = β = 1/2, this ratio equals unity, expressing the invariance of the Minkowski interval. We can also consider other cases, but first we must note one further restriction. It's clear that with u = 0, U = v this ratio must equal the inverse of the case u = v, U = 0, which implies that α + β = 1, and so the above relation can be written in the form

This quantity is invariant under the generalized Lorentz transformation with the parameter α. As an example, the case α = 1 leads to the non-standard transformation

and conversely

On this basis the invariant relation is

If we set U = 0 (thereby identifying the upper case symbols as the absolute rest frame), then the "proper time" s along the interval from the origin to the point (X,T) is given by the invariant equation with x = 0 and u = X/T. The result is

Depending on the choice of sign, this leads to one of the two relations

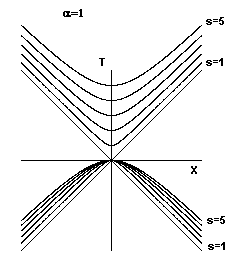
This represents two hyperbolas, each of "radius" |s|/2. If s is positive the center of the hyperbola is at the point {T = s/2, X = 0}, whereas if s is negative the center is at the point {T = −s/2, X = 0}. If we consider just the positive timelike distances, each distance corresponds to two hyperbolic branches, one of which falls outside the nullcone, and the other of which is asymptotic to the advanced lightlines plus s/2, as shown in Figure 1b.

Figure 1aFigure 1b

The loci of constant proper distance from the origin have the same hyperbolic shape with respect to every frame, differing only by the scale factor 1/(1−u²) relative to the absolute rest frame. In other words, given two observers momentarily intersecting at the origin, one at absolute rest and the other moving at u, the locus of points at a distance S (from the observers) with respect to the rest frame is identical to the locus of points at a distance s = S/(1−u²) with respect to the moving frame. For negative values of s, the figure is reflected about the x axis. For imaginary distances, interchange the x and t axes.

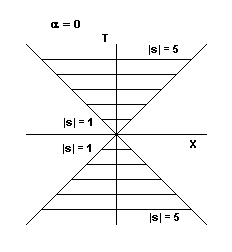
Another interesting example is the case α = 0, for which the invariant relation for intervals becomes

If we again assume U=0, then the proper timelike distances s in the (x,t) frame satisfy the relation s² = T², so the loci of equidistant points are as shown in Figure 1a.

One way of experimentally distinguishing between the cases α = 0, 1/2, and 1 is by examining the Doppler shift. The standard relativistic Doppler effect, corresponding to the case α = 1/2, is described in The Doppler Shift for Sound and Light. The case α = 0 gives a Doppler frequency ratio of precisely 1/(1−u) for light signals communicated between the absolute rest frame and a frame with speed u. This is exactly the classical Doppler effect if the receiver is stationary and the source is approaching. On the other hand, the case α = 1 gives a Doppler frequency ratio of 1+u, which is exactly the same as the classical Doppler effect if the source is stationary and the receiver is approaching. Each of these extreme cases agrees with the relativistic Doppler shift to first order, and in fact the relativistic effect is the geometric mean of these two ratios. Since the relativistic Doppler effect has been experimentally confirmed to second order, we know that α must equal 1/2, or at least be very close to 1/2, but it's interesting to note that this conclusion does not follow directly from the relativistic composition rule. It is also necessary to apply the relativity principle itself when factoring equation (1), in order to arrive at a system of complete symmetry, thereby obviating an absolute rest frame. It's interesting to speculate as to the observable effects of a slight deviation of α from the relativistic value of 1/2. It should be emphasized again that this is not the usual simultaneity convention parameter, which has no operational effect. In contrast, the α parameter does have operational effects, so it's not simply a matter of convention.

Although the generalized Lorentz transformation with α significantly different from 1/2 is evidently not applicable to translatory motion, it's conceivable that it might apply to some other kind of extrinsic change. Obviously it would need to be a variable that does have an absolute zero reference. For example, recalling that angular velocity is absolute, we might speculate that a generalized relativistic composition law applies to angular speeds. (Here we need to carefully distinguish between purely angular displacement as opposed to circular translatory displacement of the parts of an extended object.) In this case we replace (x,t) with (θ,t), and instead of v = dx/dt we focus on ω = dθ/dt, positing an invariant conversion between orientation (angular position) and time.

Recalling that the unit of angular position is the radian, which is regarded as a null dimension, we have the interesting sequence of units

This suggests that, just as velocity v is the temporal derivative of the spatial parameter x, the angular orientation θ might be regarded as the temporal derivative of a temporal parameter ξ. Conversely, ξ can be seen as the integral of angular position.

There are similarities between the angular dimension θ and a hypothetical spatial dimension that is cylindrical with a circumference of 2π. Just as in a cylindrical spatial dimension, we find that the global topology breaks the Lorentz symmetry, and there is a unique "rest frame" in which the circumference is a maximum. For relatively moving frames the instantaneous circumference is less, which implies that the angular extent of a complete circumnavigation of the rotational dimension is less than 2π. This effect is superficially similar to the angular dilation that occurs with respect to ordinary rotation, which actually consist of coordinated translations of the components of extended objects. However, this hypothetical cylindrical dimension is distinct from the space of ordinary rotations, because it can be circumnavigated at a single point in space. The possibility of three cylindrical dimensions, corresponding to the observed three degrees of angular freedom (Euler angles), with generalized Lorentz covariance, is discussed in the note on Curled-Up Dimensions.

Return to MathPages Main Menu