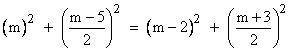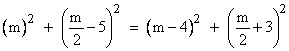On  f(x² + y²) = f(x)² + f(y)²

Consider an integer-valued function f(k) such that f(1) is positive and

We can show that the only such function is the identity function f(k) = k. To prove this, first note that setting m = 1 and n = 0 in equation (1) and re-arranging terms gives the condition

Since the integer f(1) is positive, and the square integer f(0)² must be non-negative, it follows that f(1) must equal 1, and hence f(0) = 0. We then immediately have

for all positive integers m. Also, setting m = 1 and n = 1 in equation (1) gives

Using this result along with equation (2) gives f(4) = 4, and we can then determine f(5) from the condition

W can now make use of the smallest Pythaogrean triple to give

Since we know f(4) = 4 and f(5) = 5, this equation gives f(3)² = 9, and hence f(3) = 3. Using these results we also have

Doubling the terms of the smallest Pythagorean triple, we can now compute

Using the values of f(8) and f(10), we get f(6)² = 36 and hence f(6) = 6. In summary, we have determined that f(k) = k for all k less than 7.

Now, to generalize this procedure, suppose that f(k) = k for all k less than m, and suppose for the integer m there exist three smaller integers n,r,s such that

Applying the function f to both sides and making use of equation (1), this would imply

Furthermore, since by assumption we have f(k) = k for all k less than m, and since by assumption the integers n,r,s are each less than m, it follows that

and therefore f(m) = m. Thus we need only prove that, for every integer m greater than 6, there exist smaller integers n,r,s such that equation (3) is satisfied. To prove this, we first re-write equation (3) in the form

If we choose r with the same parity as m, then we have the following integer factorizations of both sides

Identifying the factors on the two sides of this equation, we get two conditions

Solving these for s and n, we get the integers

To make these as small as possible, while still having r smaller than m and with the same parity, we set r = m-2. Substituting this into the expressions for s and n, and inserting these back into equation (3), we arrive at the identity

Note that for every odd integer m greater than 6, the three other terms in this equation are strictly less than m. For even values of m, we can multiply through the above equation by 2², and then replace 2m with m. This gives the identity

For every even integer m greater than 6, the three other terms in this equation are strictly less than m. Therefore, using these two equations, along with equation (1), we can complete the induction step, so we have proven that f(k) = k for all integers k.

We might wonder if a similar proof can be made to work if we allow f(k) to take on real values. The value of f(0) is forced by the relation

to be either 0 or 1/2. If we let f(0) = 1/2 then we have a quadratic in f(1)

which implies that f(1) also equals 1/2. Then we have the equation

From here it's clear that setting f(k) = 1/2 for all k gives a consistent solution, and this is the only other solution besides f(k) = k (which, as shown above, is the only solution for integer functions).

Return to MathPages Main Menu