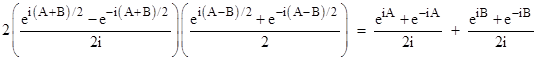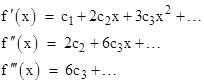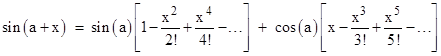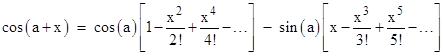From Broken Chords to Trigonometric Identities

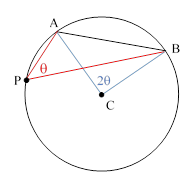
The first known systematic use of trigonometry known was by Hipparchus, who compiled a table of chords, equivalent to a table of sines, for use in astronomy. This led to the discovery and proof of many useful trigonometric identities. However, many theorems equivalent to what we would call trigonometric theorems were known previously. One interesting example is the “law of broken chords”, which later Arabic scholars attributed to Archimedes (although the original work by Archimedes is lost). They reported that Archimedes gave several different proofs of this theorem. To describe this, we will make use of a very elementary “lemma”, well known in ancient times, that the angle sub-tending an arc of a circle from any point on the circle is half the angle subtended from the center of the circle, as illustrated in the left-hand figure below.

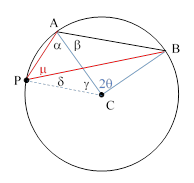
In terms of the angles marked on the right-hand figure, we see that this lemma is an immediate consequence of the fact that PCA is isosceles so we have μ + δ = (π – γ)/2, and PCB is isosceles so we have δ + θ = (π – γ)/2, from which we get μ = θ, which was to be shown.

Now, the law of the broken chord is illustrated in the figure below.

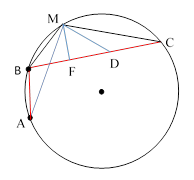
The “broken chord” consists of the two chords AB and BC, and we stipulate that BC is the larger of the chords. Archimedes theorem is that if M is the mid-point of the arc AC, and we drop the perpendicular from M to BC at the point F, then AB + BF = FC.

To prove this, let D be the point on BC such that DC = AB. Now, by the preceding lemma, since the angles BAM and BCM both subtend the same arc BM from points on the circle, those angles are equal to each other. Also, since M is the midpoint of the arc AC, we know that AM = CM. Furthermore, by construction, DC = AB. Therefore, the triangles DCM and BAM are congruent, so we have MB = MD, and hence FB = FD. Consequently AB + BF = DC + FD = FC, which was to be proven.

Now, this theorem of Archimedes can be interpreted in trigonometric terms. Let the central arc subtended by the chord MC equal 2α, and let the central arc subtended by the chord MB be 2β. Since M is the midpoint of the arc AC, we also know that the central angle subtended by AM is 2α, and therefore the central angle subtended by the chord AB is 2α – 2β. Thus for a unit circle we have MC = 2sin(α), MB = 2 sin(β), and AB = 2sin(α−β). Furthermore, making use of the lemma again, we know the angle MBC equals α and the angle MCB equals β, so we have BF = MB cos(α) and FC = MC cos(β). In these terms, the law of broken chords is

Hence dividing through by 2 and re-arranging terms, this gives the trigonometric identity

Over 18 centuries years later, European mathematicians such as Francois Viete worked more explicitly in terms of trigonometric functions to derive other identities, although the reasoning was still essentially geometrical. For example, around 1593 Viete considered the figure below.

By construction we have γ = α – β, and by the lemma we see that the angle DAB equals γ/2. Therefore, noting that AB = 2sin((α+β)/2), we can immediately write the equality

More powerful algebraic methods began to be developed just over a hundred years later, around 1700, when De Moivre and others employed imaginary and complex numbers involving i = √-1 to arrive at relations such as [cos(x) + i sin(x)]ⁿ = cos(nx) + i sin(nx). By 1740, Euler was able to express the trigonometric functions in terms of exponentials as

This led to new and more efficient demonstrations of many trigonometric identities.  Jacques Hadamard said "The shortest path between two truths in the real domain sometimes passes through the complex domain", and this is certainly true when it comes to finding trigonometric identities such as

Given the left-hand expression, determining the right-hand expression is just a matter of multiplying through using the exponential forms of sine and cosine as follows

On the other hand, if we were given the right-hand expression, it would be less obvious that it factors as shown on the left side. In general the task of factorization seems to be more difficult than the task of multiplication. In a sense, asking for a "converted" version of sin(x) + sin(y) is analogous to asking for the factors of an integer, whereas asking for a converted version of 2sin((x+y)/2)cos((x−y)/2) is analogous to asking for the product of two integers. A proof (or disproof) of a given proposition is generally easier than constructing the proposition in the first place. This is similar to integral formulas.  Given the integral of a function it's usually easy to differentiate and find the function, but finding the integral from the function is often much more difficult.  In this sense, differentiation is to multiplication as integration is to factoring.  Very often in situations like this we take the approach of just differentiating every function we can think of, and write down the derivatives in a table along with the function.  Then to find the integral of a function we just look for that function in the derivative column of our table.  A similar approach was used to construct the tables of standard trigonometric identities.

This approach have very wide applicability.  Jacobi once said "Always invert!", which is how he made most of Legendre's work on elliptic integrals obsolete.  (This same approach works outside of mathematics too.) Combining Hadamard and Jacobi's comments, we can say that, in general, two very powerful rules are for producing useful results quickly are: (1) Use complex numbers, and (2) always invert. 

Another general and highly effective approach to determining algebraic and trigonometric identities is to express the functions as power series.  The realization that a large class of functions can be represented as power series (especially by Isaac Newton in the late 1600’s) was one of the most significant turning points in the development of modern mathematics. To show how this can be applied to the derivation of trigonometric identities, suppose we want to find an expression for sin(a+b) in terms of the sines and cosines of the individual numbers a and b.  For a general power series

we have the derivatives

and so on.  It's clear that the nth derivative at x = 0 is simply (n!)c_n, and so the nth coefficient c_n equals the nth derivative divided by n!.  Now recall that the derivative of the sine is the cosine, and the derivative of the cosine is the negative sine, so we can expand the function f(x) = sin(a+x) around the point x=0 as follows

By the same reasoning we can write down the power series for cos(a+x) expanded about the point a:

Not surprisingly, these expressions reduce to the familiar power series for sin(x) and cos(x) if we set a = 0.  Now, suppose we collect terms in the series for sin(a+x) according to whether they contain a sine or a cosine.  This gives

We immediately recognize the quantities inside the brackets as the cosine and sine of x, so we have the trigonometric identity

Similarly if we separate the terms of the series for cos(a+x) we arrive at

which gives the identity

This shows how it’s often possible to deduce closed-form identities from consideration of the infinite series expansions of the functions involved.

Return to MathPages Main Menu