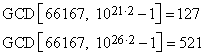A Method Of Factoring Based On 1/N

Here's an interesting little algorithm for determining the prime factors of a natural number N = pq. For any positive integer N let T(N) denote the period of the base-B expansion of 1/N. If N = pq we know that

Putting g = GCD[T(p),T(q)] we have T(N) = T(p)T(q)/g. Thus, for some factorization T(N) = abg we have T(p) = ag and T(q) = bg, and so

which is easily computed using the Euclidean algorithm and modular exponentiation.

To illustrate this method with a simple example, suppose we want to know the factors of N = 1517. The base-10 expansion of 1/1517 has period T(1517) = 15, so we take the factorization 15 = (3)(5)(1), i.e., with a = 3, b = 5, g = 1, and we immediately compute

Admittedly this is a simple example because T(N) has only one non- trivial factorization with g = 1, and T(p) happens to be coprime to T(q).

For a more general example, take the case N = 66167. Here we can readily compute T(66167) = 1092, which has the factorization

Thus, 1092 can be expressed as a product abg in several different ways. Trying each of the multiplicative partitions of 1092 we come finally to 1092 = (21)(26)(2). This represents the condition that T(p) = ag = 42 and T(q) = bg = 52, so T(p) and T(q) are not coprime in this case. On this basis we compute

which gives the factors of 66167. Of course, once we have one of these factors, the other is known, so we really only need to try each divisor d of T(N) until finding one for which GCD[N, B^k - 1] is a non-trivial factor of N.

Needless to say, this method assumes that we can factor T(N). If T(N) is really difficult to factor, we can try applying the method recursively if we can factor T(T(N)), and so on.

More seriously, the method also works only if we can determine the period of the expansion of 1/N. This is equivalent to determining, for some base integer B, the period of the sequence 1, B, B², B³, ... modulo N. In other words, we seek the smallest integer k such that B^k = 1 (mod N). Of course this can be done, in principle, by an exhaustive search, but that's no better than just performing trial divisions on N.

Another way to approach the problem of determining the period of this sequence is to think of the waveform such as is produced by, for example, a violin. The sound produced by a violin has a very odd characteristic shape which determines its timbre. It may look something like this

When we pluck the violin string it repeats this cycle over and over again. If we translate this pattern into pressure pulses in the air and listen to it, we hear a tone. Actually we hear a set of harmonics, and the frequencies are dependant on the cycle length. One of the harmonics will be dependant on the overall cycle length. Digital music recording systems use Fourier analysis to break down a sequence of discrete values into amplitudes and frequencies, so we might think about using this same technique to determine the frequencies in the sequence 1, m, m², etc.

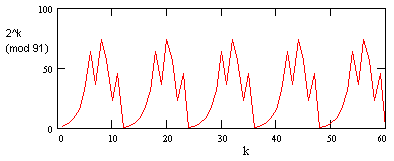
To illustrate, suppose we want to factor N = 91. The figure below shows 2^k (mod 91) as k ranges from 0 to 60.

Naturally this waveform has strong harmonics at frequencies of 7 and 13 because they are the factors of 91. Thus, by examining the spectral signature of 2^k (mod N) we could, in principle, determine the factors of N.

Of course, if N is large the period of 1/N can be extremely large, so it wouldn't be practical to compute each number 1, m, m², m³, and try to "listen" to it using Fourier analysis. However, we don't really need to sample the signal at every point. For example, there are infinitely many points on a violin waveform, but we only sample the wave at a limited number of points, and subject those points to discrete FFT to reconstruct the signal. Similarly we can sample the sequence of m powers just every kth term, i.e., 1, m^k, m^2k, m^3k, and so on. We can compute these values over a large range, so that we cover several cycles, and from these samples we can try to discern the underlying frequency.

The reason it's so much harder to find the frequency from this type of signal, as opposed to a violin signal, is that a violin waveform is fairly "smooth", whereas the m-sequence is exponential, so when we repeatedly truncate it (mod N) we destroy (or actually, disguise) information very quickly. I say "disguise" because it's still just a simple exponential function, in spite of the fact that it appears scrambled when viewed modulo N.

So this is what we might try to do: Take a very sparse sample from the sequence of powers of m (mod N), and "listen" to it in various ways, and with various kinds of filters and amplifiers, etc, trying to extract the faint trace of the underlying periods, from which the factorization of N follows. It's not too hard for relatively small numbers; in fact, if we run the scaled m-sequence through a sound card and literally listen to the expansion of 1/N, we can literally hear the frequencies. It's neat. But for larger numbers the sound turns to "white noise". I haven't been able to think of a set of filters or amplifiers to unscramble the (mod N) effect for really large numbers. Presumably it's impossible, but I don't know how to prove it.

Postscript: The integer factoring method discussed above actually forms the basis of what is called "Shor's algorithm" in the field of quantum computing. See the note on entitled Can Schrodinger's Cat Factor Numbers? for more on this topic.

Return to MathPages Main Menu