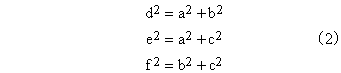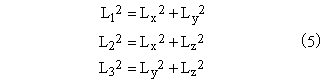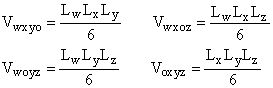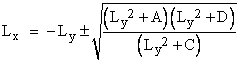Heron's Formula For Tetrahedra

In another article we gave a very direct derivation of Heron's formula based on Pythagoras's Theorem for right triangles. However, we might also observe that Heron's formula is essentially equivalent to Pythagoras' Theorem for right tetrahedra. For a right tetrahedron with vertices (0,0,0), (a,0,0), (0,b,0), and (0,0,c), the base and height of the "hypotenuse" are

where (by similar triangles) h = ab/(Base) is the distance from the origin to the base, so we have

Thus if B,C,D denote the areas of the three orthogonal faces of a right tetrahedron with orthogonal edge lengths a,b,c, and if A denotes the area of the "hypotenuse face", we have

where B = ab/2, C = ac/2, and D = bc/2. This is essentially Heron's formula. To make this explicit, note that the edges of the hypotenuse face d,e,f are directly related to a,b,c according to the Pythagorean relations

so we can express the areas B,C,D in equation (1) in terms of d², e², and f² to give Heron's formula explicitly.

It might seem as if this derivation does not apply to obtuse triangles, because the "hypotenuse face" of a right tetrahedron is necessarily acute (i.e., each of its angles must be less than 90 degrees). However, any triangle can be the hypotenuse face of a right tetrahedron, provided the orthogonal edge lengths and areas are allowed to be imaginary. Thus for any values of d,e,f we can solve equations (2) for the orthogonal edges of the right tetrahedron whose hypotenuse is the triangle with the edges lengths d, e, f. This gives

For example, suppose we want the area of a triangle with edge lengths 8, 5, and 5, which is an obtuse triangle. Substituting these into the above equations gives

so the "c" leg has imaginary length. Consequently, two of the three orthogonal faces (those given by ac/2 and bc/2) are also imaginary. However, these areas only appear squared in the Pythagorean formula for right tetrahedrons, so we're guaranteed to get a real area for the hypotenuse face. As Hadamard said, "The shortest path to any truth involving real quantities often passes through the complex plane".

I honestly wouldn't be surprised if the ancient Greeks were aware of the connection between the generalized Pythagorean theorem and Heron's formula, but refrained from presenting it in that form because of difficulties with interpreting the obtuse case. Recall that Descartes, for one, believed the ancient Greeks had discovered most of their theorems analytically by means of coordinate geometry and algebra, but concealed their methods, presenting them in synthetic form, so as to make the results seem more daunting and impressive to the uninitiated. (See the note on Prisca Sapientia.) It has always seemed doubtful that Heron's formula was discovered via the thought process of Heron's proof, which is absurdly circuitous. In any case, this is a nice example of how imaginary numbers can arise naturally in dealing with questions of purely real quantities.

As for higher dimensional simplexes, there is no complete generalization of Heron's formula giving the volume of a general tetrahedron in terms of the areas of its faces, because the face areas don't uniquely determine the volume (in contrast to the case of triangles, where the three edge lengths determine the area). However, it is possible to derive a "Heron's formula" for tetrahedrons if we restrict ourselves to just those that would fit as the "hypotenuse face" of a right four-dimensional solid. (Notice that every triangle is the face of a right tetrahedron, which explains why Heron's formula is complete for triangles).

To review, remember that Heron's formula for triangles is essentially equivalent to Pythagoras' Theorem for right tetrahedrons. Let's let A_xyo, A_xoz, and A_oyz denote the areas of the three orthogonal faces of a right tetrahedron, and A_xyz denote the area of the "hypotenuse face", so we have

Now if we let L_x, L_y, L_z denote the three orthogonal edge lengths of the tetrahedron, then the areas of its orthogonal faces are simply

and so equation (3) can be re-written in the form

Furthermore, the three edges L₁, L₂, L₃ of the hypotenuse face are directly related to L_x, L_y, L_z by the two-dimensional Pythagorean theorem

Equations (5) are three linear equations in the three squared edge lengths, so we can solve for these squared lengths in terms of L₁, L₂, and L₃, and then substitute these into equation (4) to give the ordinary Heron's formula for triangles, as before.

Now, we can do the same thing for tetrahedrons based on the generalized Pythagorean theorem for volumes of right four-dimensional solids

If we let L_w, L_x, L_y, L_z, denote the orthogonal edge lengths of the four-dimensional solid, then the volumes of the four orthogonal "faces" are simply

so equation (3') can be rewritten as

Furthermore, the four areas A₁, A₂, A₃, A₄ of the hypotenuse "face" are directly related to L_x, L_y, L_z by the three-dimensional Pythagorean theorem (4)

Thus, given the four face areas A₁, A₂, A₃, A₄, we have four equations in the four unknowns L₂, L_x, L_y, L_z, so we can solve for these values and then compute the volume of the tetrahedron using (4').

At this point people usually turn away from this approach, for two reasons. First, everything we're doing is restricted to the "special" tetrahedrons that can serve as the hypotenuse of a "right" four-dimensional simplex, so we're certainly not going to end up with a general formula applicable to every tetrahedron (as is clear from the fact that we have only four independent edge lengths here, whereas the general tetrahedron has six). General formulas giving the volume in terms of the edge lengths do exist, such as the one give by the Italian painter Piero della Francesca. Of course, all such formulae can be traced back to the well-known determinant expression for volumes.

The second reason that people usually give up on equations (5') is that they are somewhat messy to solve, since they are non-linear in the lengths. Still, we might decide to press on anyway. It turns out (after extensive algebraic manipulation) that we can reduce (5')

to a single quartic in the square of any of the four edge lengths L_w, L_x, L_y, or L_z. Arbitrarily selecting L_y, and letting A,B,C,D denote 4 times the squares of the face areas (i.e., the left hand sides of equations (5')), we can express the quartic in x = L_y² with coefficients that are functions of B and the elementary symmetric polynomials of A,C,D

In these terms the quartic for x = L_y² is

Of course, the analogous quartics can be given for L_w², L_x², and L_z², but once we have any one of them we can more easily compute the others. For example, given L_y we can compute L_x from the relation

and the values of L_w and L_z follow easily, allowing us to compute the volume using equation (4'). It would be nice if we could express the volume as an explicit function of the face areas, but I don't know if such a formula exists.

In the preceding discussion we developed a tetrahedral version of Heron's formula for a restricted class of tetrahedra, namely those that can serve as the hypotenuse of a "right" four-dimensional simplex, but there are other special classes of tetrahedra that possess interesting volume formulas. The one that gives the closest analogue to Heron's formula is the class of tetrahedra whose opposite edges lengths are equal. Thus there are only three independent edge lengths, and each face of the tetrahedron is identical. Letting (a,f), (b,e), and (c,d) denote the pairs of opposite edge lengths, we can set a = f, b = e, and c = d in the basic determinant expression for the volume, or equivalently in Piero della Francesca's formula, and we find that the resulting expression for the squared volume factors as

which is certainly reminiscent of Heron's formula for the area of each face

This also shows that if each face is an identical right triangle, the volume is zero, as it must be, since four such triangles connected by their edges to give a tetrahedron necessarily all lie flat in the same plane:

Obviously we can construct a regular tetrahedron with equilateral triangles of the same area as these right triangles, and the volume is , which illustrates the fact that the face areas of a tetrahedron do not in general determine it's volume.

Return to MathPages Main Menu