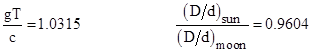|
Two Geophysical Coincidences |
|
|
|
|
|
|
|
Which of the following coincidences is more impressive? |
|
|
|
(1) gT ≈ c The acceleration of gravity at the earth's surface multiplied by one period of the earth's orbit equals the speed of light. |
|
|
|
(2) (D/d)sun ≈ (D/d)moon The diameter over the distance for the sun equals the same ratio for the moon. |
|
|
|
Needless to say, these equalities are only approximate. Numerically we have roughly |
|
|
|
|
|
|
|
Historically coincidence (2) has certainly received more attention, since the astonishing precision of the match is displayed so vividly during solar eclipses. In contrast, it's hard to think of any physically perceivable consequences of coincidence (1). On the other hand, the appearance of the physical constant c in (1) seems quite remarkable. |
|
|
|
An interesting related question is whether such coincidences are, in effect, compounded by the fact that they apply to – and only to – our own planet Earth, a planet distinguished by several other seemingly unique properties, not least of which is its being the only site (as far as we know) of the spontaneous emergence of life. Admittedly, judging the significance of events after they have occurred is a very tricky undertaking. (Something improbable is bound to happen.) Nevertheless, the apprehension of "coincidences" and patterns is one of the foundations – maybe even the foundation – of rational thought (as well as much irrational thought.) |
|
|
|
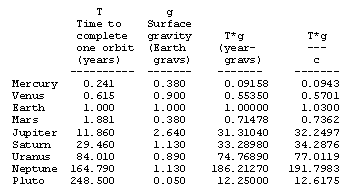
In any case, on the subject of coincidence (1), it’s interesting to review the orbital periods and surface gravities of the nine planets as listed in the table below. |
|
|
|
|
|
|
|
The product Tg has units of velocity, so we can express it in dimensionless form if we divide it by some standard velocity, such as c (the speed of light). The right hand column lists these dimensionless values for the nine planets. As can be seen, Tg/c ranges from about 1/10 up to nearly 200. |
|
|
|
For a planet of mass m and radius r in a roughly circular orbit of radius R around a star of mass M, the surface gravity is about g = Gm/r2 (where G is Newton's gravitational constant) and the period of revolution is about T = 2π r3/2 / sqrt(GM). Therefore, the product gT for this hypothetical orbiting planet is |
|
|
|
|
|
|
|
For example, the mean distance from the Earth to the Sun is about R = 1.49x1011 meters, the Earth's mass is about m = 5.98x1024 kg, the Earth's radius is about r = 6.37x106 meters, and the Sun's mass is about M = 2.0x1030 kg. Newton's constant is 6.67x10-11 Nm2/kg2, so we have gT approximately 3x108 m/sec, confirming that gT/c is about 1 for the Earth. |
|
|
|
Are there any physical or biological reasons for us to expect to find ourselves on a planet for which gT/c is close to 1? Would there be any special obstacles to the development of life on a planet orbiting a star if the value of gT/c was as great as, say, 10, or as small as 1/10? |
|
|
|
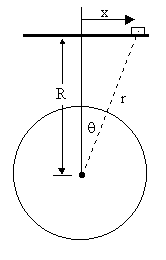
A somewhat related coincidence (of a different sort) is the fact that the period of a circular orbit around a gravitating body is identical to the period of a tableau pendulum at the same altitude. Consider a flat table at a height R from the center of a gravitating body, and suppose a frictionless puck is placed on this table, as illustrated below. |
|
|
|
|
|
In the small-angle approximation we have cos(θ) ~ 1 and sin(θ) ~ θ, so the equation of horizontal motion for the puck is GM/r2θ = - rθ" where M is the mass of the gravitating body. Thus we have |
|
|
|
|
|
|
|
which has the solution θ = A cos(ωt) where |
|
|
|
|
|
|
|
The period of this oscillation is T = 2π/ω, which is identical to the period of a circular orbit of radius r, so we could substitute the period of a tableau pendulum at the Earth's distance from the Sun in place of the Earth's orbital period in the first geophysical coincidence noted above. |
|
|