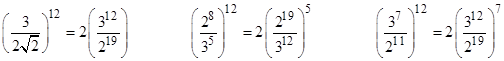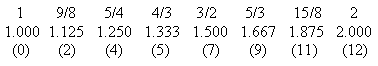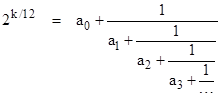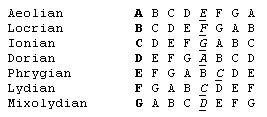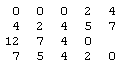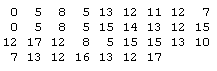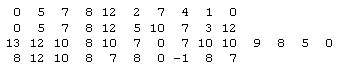Accidental Melodies

The range of acoustic tones perceivable by humans extends roughly from 20 Hz up to 20,000 Hz (cycles per second), which is a factor of 1000. Thus, noting that 2¹⁰ = 1024, the audible range of frequencies represents about 10 doublings. The harmonic association of tones with doubled or halved frequencies is so strong that we tend to regard all tones with frequencies 2ⁿ ν as "the same" in some sense. As a result, we conceive of the audible range of tones in terms of 10 "copies" of the same sequence of tones, each of which covers frequencies up to a factor of 2, say from ν up to 2ν for some arbitrary fixed frequency ν.

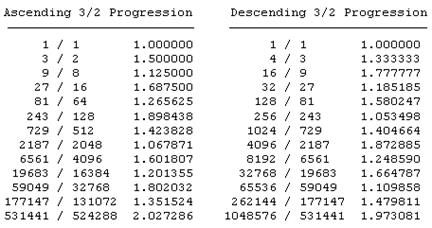
Within each of these ranges there exist other harmonic associations, not as strong as the 2:1 harmonic, but strong enough to make the combinations of certain tones aesthetically pleasing. The most notable is the 3:2 harmonic. (Incidentally, this harmonic features in the gravitational coupling between the rotations and revolutions of the planet Mercury.) Beginning with some basic frequency ν, we can increase this successively by the ratio 3/2, and divide by factors of 2 as necessary to express the results in the range 1 to 2. This gives the sequence of frequencies in the left-hand columns below. On the other hand, beginning from the same basic frequency, we can successively divide by 3/2, and multiply by factors of 2 as necessary to express the results in the range 1 to 2. This gives the sequence of frequencies listed in the right hand columns.

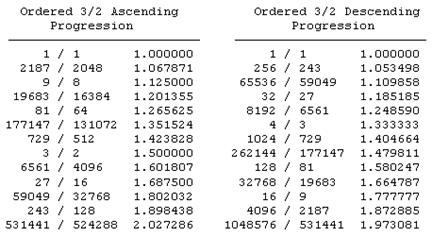
In each of these sequences, on the 12th step we arrive nearly at twice the initial base tone, differing by only about 1.36%. (I've allowed the last entry in the left hand columns to exceed 2, since it is very nearly equal to 2.) This occurs because 3¹² and 2¹⁹ happen to be nearly equal. If we re-arrange the entries in these columns so that the frequencies are in ascending order, we get the results shown below.

These two harmonic progressions give two very similar sequences of 12 tones. If we take the geometric mean of each pair of corresponding tones, we get the sequence of squared frequencies listed below, along with the ratios of consecutive frequencies.

There are only three distinct ratios between consecutive tones in this sequence, namely

To the approximation that 2¹⁹/3¹² ~ 1, each of these represents an approximation of the 12th root of 2, as shown by the identities

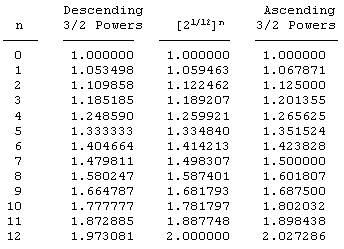
Therefore it's not surprising that the (normalized) ascending and descending powers of 3/2 closely bracket the geometric progression of the powers of 2^1/12, as shown in the table below.

In addition to the 3/2 harmonic, several other fundamental harmonics are approximated by elements of these sequences. The most prominent are the tones with n = 0, 2, 4, 5, 7, 9, 11, and 12, which correspond approximately to the harmonic ratios 1, 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, and 2 respectively. These comprise the basic 8-tone scale, with frequencies proportional to

The numbers in parentheses signify the tone from the previous table that most nearly approximates each of these frequencies. Clearing the fractions, the frequencies are proportional to

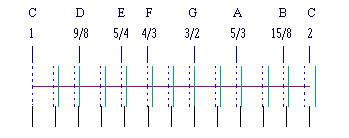
The figure below shows the logarithms of the (normalized) ascending and descending progression of powers of 3/2 as the dashed and solid central lines, and the powers of the 12th roots of 2 as the bottom row of lines, and the eight harmonic tones as the top row of lines.

Since this is a logarithmic scale, the 12th roots of 2 are uniformly spaced on the interval. Using these tones rather than the exact harmonic rational fractions gives the "equally-tempered" scale used in most modern music, particularly keyboard music. This strictly geometric scale was advocated by Bach and others in the 18th century to enable smooth modulation from one key to the next in the course of a single composition. It might have been more descriptively named the logarithmic scale.

Since the 12th root of 2 is irrational, none of these terms in the "equally-tempered" progression correspond exactly with any rational harmonics. However, each number of the form 2^k/12 for k = 0, 1,.., 12 can be expressed as a continued fraction of the form

The first several coefficients for the continued fractions of the twelve equally-tempered semi-tones are listed below.

The eight harmonic tones are given by the first or second convergents, i.e., for n = 0, 2, 3, 5, 7, 9, 11, and 12 we have [1;0], [1;8], [1;3,1], [1;2,1], [1;2], [1;1,2], [1;1,7], [2;0].

Our familiar eight-tone major scale is really just one of "modes" that were developed in Western Europe beginning in the Middle Ages. They were originally defined by the Roman Catholic Church as part of the singing of the psalms. Each mode had an eight-tone scale with a designated "reciting note", around which most of the words were sung (or chanted) and a "final note" on which the song was to end. The full set of seven modes (not counting the "hypo", aka plagal, modes, which differed only in range) were as listed below

For each mode the "finalis" is listed in bold type, and the reciting note (also called the tenor) is underlined. The original formulation of musical modes for church music is attributed to St. Ambrose (c. 340-397), who set down the rules for what came to be called the Dorian, Phyrgian, Lydian, and Mixolydian modes. Interestingly, the Ionian and Aoelian modes were apparently not formalized until the 16th century, by a Swiss monk named Henry of Glarus (1488-1563). (The Locrian mode was hardly ever used, because of its unpleasant tonic chord, and is included on the list only for completeness.) Of all these seven modes, only two survive today, the Ionian and Aeolian, which we call the major and minor scales.

Most common melodies make use of only tones that are among the seven main tones (up to powers of 2) of the key in which they are written. For example, the well-known tune "Row, Row, Row Your Boat" is written in the major mode, whose main tones from the full 12-tone scale are 0, 2, 4, 5, 7, 9, 11, and the melody consists of the sequence of tones

The note n = 12 is just double the frequency if n = 0, so we don't count this as a distinct tone.  Hence this melody uses just five of the seven distinct tones in the major key, namely, 0, 2, 4, 5, and 7. More sophisticated melodies make use of all seven of the major tones in the chosen key.

Furthermore, a composer sometimes calls for a note that is not even in the chosen key. Such a note is prefixed with its own sharp (♯) or flat (♭) symbol, and it's called an accidental. One example of a "highly accidental" melody is the title song from the 1963 movie "From Russia With Love" (composed by Lionel Bart), which consists of the following sequence of tones:

Examining this modulo 12, we find that there is at least one appearance of each of the tones 0, 1, 2, 3, 4, 5, 7, 8, 10, and 11. In other words, of the twelve distinct semi-tones in the full equally-tempered scale, this melody invokes ten of them (the missing tones are 6 and 9), so it is what I would call a highly accidental melody.

An even more impressive example is "The Shadow of Your Smile", composed by Johnny Mandel for the 1965 movie "The Sandpipers". This song won the Academy Award for Best Original Song, presumably because the Academy members were appreciative of the fact that the melody invokes eleven of the twelve tones in the full equally-tempered scale. The sequence of tones in this melody is

Again evaluating these tones modulo 12, we see that the only one of the twelve tones in the scale not touched is n = 6. Naturally the works of Bach include compositions in which he systematically progressed through each semi-tone of the equally-tempered scale, but I'm not aware of any simple popular melody that contains all twelve semi-tones.

Return to MathPages Main Menu