Magnetism and Earnshaw's Theorem
Speaking well about Homer is not a thing you have mastered, it's a divine power that moves you, as a "Magnetic" stone moves iron rings. (That's what Euripides called it; most people call it "Heraclian".) This stone not only pulls those rings, if they are iron, it also puts power in the rings, so they in turn can do just what the stone does- pull other rings - so that there is sometimes a very long chain of iron pieces, hanging from one another. And the power in all of them depends on this stone. - Socrates in Plato's "Ion" c. 380 BC
Magnetism has been known since ancient times. The magnetic property of lodestone (Fe3O4) was mentioned by the Greek philosopher Thales (c. 500 BC), and the Greeks called this mineral "Magnetic", after the province of Magnesia in Thessaly where it was commonly found. It was also found in the nearby province of Heraclia, which is presumably why Socrates says that most people called the stone "Heraclian". Apparently we have the great dramatist Euripides to thank for not having to pronounce the electro-heraclian field.
About 1000 AD the Chinese began to use lodestone as a compass for finding directions on land, and soon afterwards Muslim sailors were using compasses to navigate at sea. Europeans began using magnetic compasses for navigation around 1200 AD, probably bringing the idea back from the Crusades. The first scientific study of magnets was apparently by the English physician William Gilbert in 1600, who is credited with "discovering" that the Earth itself is a magnet. After Gilbert, the subject languished for almost 200 years, as the attention of most scientists turned to gravitation and working out the consequences of Newton's great synthesis of dynamics and astronomy. Not until 1785 was the subject taken up again, first by the Frenchman Charles Coulomb, then by Poisson, Oersted, Ampere, Henry, Faraday, Weber, and Gauss, culminating in Maxwell's classical synthesis of electromagnetic theory in 1875.
However, despite the great achievements of these scientists, no satisfactory understanding of the various kinds of magnetic behavior exhibited by different materials was achieved. Only with the advent of quantum mechanics in the 1920's did it become possible to give a coherent account of the main magnetic properties of materials. It's a surprisingly complex subject, but we can give a broad outline of the modern explanations of magnetic phenomena.
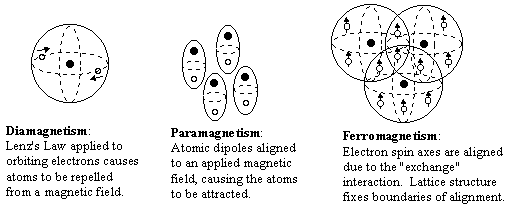
The three main types of magnetic behavior exhibited by material substances are called diamagnetism, paramagnetism, and ferromagnetism. The first two can be explained in terms of the magnetic fields produced by the orbital motions of the electrons in an atom. Each electron in an atom can be regarded as having some "orbital" motion about the nucleus, and this moving charge represents an electric current, which sets up a magnetic field for the atom, as shown below.
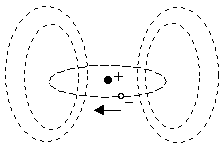
Many atoms have essentially no net magnetic dipole field, because the electrons orbit the nucleus about different axes, so their fields cancel out. Thus, whether or not an atom has a net dipole field depends on the structure of the electron shells surrounding the nucleus.
In broad terms, diamagnetism and paramagnetism are different types of responses to an externally applied magnetic field. Diamagnetism is a natural consequence of Lenz's law, according to which the electric current resulting from an applied field will be in the direction that opposes the applied field. In other words, the induced current will flow in the direction that creates a field opposite to the applied field, as illustrated below.
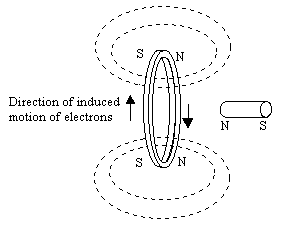
Conservation of energy implies that a force is required to push the magnet through the ring, thereby setting up the flow of current (in the opposite direction of the electron motion). Hence there is a repulsive force between the magnet and the conducting ring. Likewise when an atom is subjected to an applied magnetic field, there is a tendency for the orbital motions of the electrons to change so as to oppose the field. As a result, the atom is repelled from any magnetic field. Notice that this is true regardless of the polarity of the applied field, because the induced "currents" (i.e., the induced changes in the orbital motions of the electrons) invariably act to oppose the applied field. This phenomenon is present in all substances to some degree, but it is typically extremely small, so it is not easily noticed. It is most evident for elements whose atoms have little or no net magnetic moment (absent an externally applied field). Among all the elements at ordinary room temperatures, bismuth has the strongest diamagnetism, but even for bismuth the effect is extremely weak, because the currents that can be established by the electron orbital motions are quite small. It's possible, however, to construct a perfect diamagnet using superconductivity. A superconductor is, in many respects, like a quantum-mechanical atom, but on a macroscopic scale, and it can support very large currents. In accord with Lenz's Law, these currents oppose any applied field, so it's actually possible to achieve stable levitation of a permanent magnet over a superconductor.
In view of Lenz's Law, it might seem surprising that any material could actually be attracted to a magnetic field, but in fact there are many such substances. This is due to the phenomena called paramagnetism. Unlike the atoms of diamagnetic materials, the electrons of atoms in paramagnetic materials are arranged in such a way that there is a net magnetic dipole due to the orbital motions of the electrons around the nucleus. Thus, each atom is a small permanent magnet, but the poles tend to be oriented randomly, so a macroscopic sample of the substance usually has no net magnetic field. When such a substance is subjected to an external magnetic field, there is (as always) a small diamagnetic effect on the orbital motions of the electrons, tending to cause a repulsion (as explained above), but there is also a tendency for the individual atomic dipoles to become aligned with the imposed field, rather than being oriented randomly. This gives the substance an overall net magnetic dipole in the same direction as the applied field, so if the substance is located in a non-uniform magnetic field, it will be attracted in the direction of increasing field strength. This paramagnetic attraction effect is much stronger than the diamagnetic repulsion, so paramagnetism usually masks the effect of diamagnetism for such substances. However, even paramagnetism is so weak that it's often not noticed, because the thermal agitation of the atoms (at room temperature) tends to disrupt the alignment.
The last major category of magnetic behavior is called ferromagnetism. This is the phenomenon responsible for the strong magnetic properties of iron, and for the existence of permanent magnets, i.e., macroscopic substances (such as magnetite) that exhibit an overall net magnetic dipole field, even in the absence of any externally applied field. Many of the early researchers in the science of magnetism thought this was nothing but a strong and persistent form of paramagnetism, but the strength and persistence of ferromagnetism show that it is the result of a fundamentally different mechanism, an effect that is absent in merely paramagnetic substances. Whereas both diamagnetism and paramagnetism are essentially due to the atomic fields resulting from the orbital motions of the electrons about the nucleus, ferromagnetism is due almost entirely to alignment of the intrinsic spin axes of the individual electrons.
An individual electron possesses a quantum property known as "spin", which is somewhat analogous to the spin of a macroscopic object. (This analogy is not exact, and can be misleading in some circumstances, but it's useful for gaining an intuitive understanding of the magnetic properties of materials.) According to this view, an electron's charge is distributed around its surface, and the surface is spinning about some axis, so there is a tiny current loop, setting up a magnetic field as illustrated below.
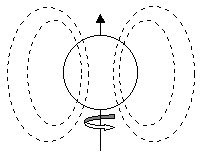
(The contribution of the nucleus itself to the magnetic field of an atom is typically negligible compared with that of the electrons.) In most elements the spin axes of the electrons point in all different directions, so there is no significant net magnetic dipole. However, in ferromagnetic substances, the intrinsic spins of many of the electrons are aligned, both within atoms and between atoms. The key question is what causes all these dipoles to be aligned, especially in the absence of an external field. It can be shown that the dipole interaction itself is not nearly strong enough to achieve and maintain alignment of the electron spin axes at room temperatures, so some other factor must be at work.
Quantum mechanics furnishes the explanation: For particular arrangements of certain kinds of atoms in the lattice structure of certain solids, the inter-electron distances within atoms and between neighboring atoms are small enough that the wave functions of the electrons overlap significantly. As a result, there is a very strong effective "coupling force" between them due to their indistinguishability. This is called an "exchange interaction", and is purely a quantum-mechanical phenomenon. There is no classical analogy. In essence, quantum mechanics tells us that there is a propensity for the identities of neighboring electrons to be exchanged, and this locks the spin orientations of the electrons together. (This is actually true only under certain circumstances. It's also possible for exchange interactions to lock the spins of neighboring electrons in opposite directions, in which case the behavior is called anti-ferromagnetism.) In order for the exchange interaction to operate, the inter-electron distances must be just right, and these distances are obviously affected by the temperature, so there is a certain temperature, called the Curie temperature, above which ferromagnetism breaks down.
Only five elements have electron shell structures that support ferromagnetism, namely, iron, cobalt, nickel, gadolinium, and dysprosium. In addition, many compounds based on these elements are also ferromagnetic. (One example is the compound Fe3O4, also called lodestone, which the ancient Greeks found lying around in Magnesia.) These are all "transition elements", with partially populated 3d inner electron shells. When magnetized, the spin axes of all the electrons in the 3d shells are aligned, not only for one atom, but for neighboring atoms as well. This gives the overall lattice of atoms a very strong net magnetic dipole. It's worth noting that this is due to the intrinsic spins of the individual electrons, not due to the orbital motions of the electrons (as is the case with diamagnetism and paramagnetism).
Recall that, for paramagnetic substances, the alignment of atomic dipoles is maintained only as long as the external field is applied. As soon as the field is removed, the atomic dipoles tend to slip back into random orientations. This is because the ordinary dipole field is not nearly strong enough to resist thermal agitation at room temperatures. In contrast, after a ferromagnetic substance has been magnetized, and the externally applied field is removed, a significant amount of magnetization remains. (This effect is called hysteresis.) In general, the electron spins of all the atoms with a suitable lattice will be locked in alignment, with or without an external field, but a real large-scale piece of a substance typically cannot be a single perfectly coherent lattice. Instead, it consists of many small regions of pure lattices, within which the exchange interaction keeps all the electron spins aligned, but the exchange interaction does not extend across the boundaries between domains. In effect, these boundaries are imperfections in the lattice. As a result, although each small domain is perfectly magnetized, the domains in an ordinary piece of iron are not aligned, so it has no significant net magnetic field. However, when subjected to an external field, there is enough extra impetus to trigger a chain reaction of alignment across the boundaries of the individual regions in the iron, causing the overall object to become a magnet. This is the phenomenon described by Socrates, when he explained how a Magnet has the power not only to attract iron, but to convey that power to the iron. He was describing a purely quantum mechanical effect, by which an applied magnetic field causes the intrinsic spin axes of individual electrons in the 3d shells of transition elements such as iron to become aligned - although he presumably wasn't thinking about it in those terms.
When the external field is removed, the various regions in the iron object will tend to slip back to their natural orientations, given the imperfections in the lattice structure, so much of magnetism of the object will be lost. However, there will be typically have been some structural re-organization of the lattice (depending on the strength of the applied field, and the temperature of the iron), so that a higher percentage of the domains are aligned, and this re-structuring of the lattice persists even after the external field is removed. This accounts for the hysteresis effect, by which a piece of iron acquires some permanent magnetism after having been exposed to a strong field. In order to create a strong permanent magnet, a piece of ferrous material is heated to a molten state, and then placed in a strong magnetic field and allowed to cool. This creates a lattice structure with very few magnetic imperfections in the lattice, so the electron spins are naturally locked in alignment throughout the material. Not surprisingly, if a magnetized piece of iron is struck with a hammer, it's possible to scramble the domains and thereby de-magnetize the object.
In summary, the three main kinds a magnetism are illustrated schematically in the figures below.
One of the most common questions about permanent magnets is whether there exist a stable and static configuration of permanent magnets that will cause an object to be levitated indefinitely. Obviously the levitation itself is not a problem, because many magnets have fields strong enough to lift their own weight. Equilibrium is also not a problem, because there is obviously a configuration at the boundary between falling and rising. The problem is stability. In order to have stability, there must be a restorative force counter-acting any displacement away from the equilibrium point.
We need to be careful when considering this question, because, as discussed above, there are several kinds of magnetic behavior exhibited by different substances in different circumstances. We can certainly achieve stable levitation with a superconductor, which is really just a perfect diamagnet. In fact, even at room temperatures, it is possible to use the diamagnetic property of a substance like bismuth to achieve (marginal) stability for magnetic levitation. Of course, in such a case, the paramagnet is too weak to do the actual levitating; it just provides a small window of stability for an object that is actually being lifted by ferromagnetic effects. But if we set aside the phenomenon of paramagnetism, which is a constantly self-adjusting field, and focus strictly on fixed fields as are produced by ferromagnets, can we achieve stable static levitation?
In 1842, Samuel Earnshaw proved what is now called Earnshaw's Theorem, which states that there is no stable and static configuration of levitating permanent magnets. (See Earnshaw, S., On the nature of the molecular forces which regulate the constitution of the luminiferous ether., 1842, Trans. Camb. Phil. Soc., 7, pp 97-112.) The term "permanent magnet" is meant to specify ferromagnetism, which is truly a fixed magnetic field relative to the magnet. In contrast, the phenomena of diamagnetism is not really "permanent", both because it requires the presence of an externally applied field, and more importantly (from the standpoint of Earnshaw's theorem) because the diamagnetic field constantly adapts to changes in the applied external field. This is why stable diamagnet levitation (of which superconductors provide the extreme example) is possible, in spite of Earnshaw's theorem.
It's worth noting that Earnshaw's theorem - ruling out the possibility of static stable levitation - presented scientists at the time with something of a puzzle, if not an outright paradox, because we observe stable configurations of levitating objects every day. For example, the book sitting on my desk is being levitated, and some force is responsible for this levitation. Admittedly it may not have been clear in Earnshaw's day that the book's interaction with the desk was via electromagnetic forces, but Earnshaw's theorem actually applies to any classical particle-based inverse-square force or combination of such forces. Since we observe stable levitation (not to mention stable atoms and stable electrons), it follows from Earnshaw's theorem that there must be something else going on, viz., we cannot account for the stable structures we observe in nature purely in terms of classical inverse-square forces, or even in terms of any kind of classical conservative forces. In order to explain why stable atoms are possible (i.e., why the electrons don't simply spiral in and collide with the protons) and why other stable structures are possible, it's necessary to invoke some other principle(s). Something like quantum mechanics and the exclusion principle is required.
The proof of Earnshaw's theorem follows closely from Gauss's law. Indeed this accounts for the generality of its applicability. To consider the simplest case, suppose we wish to arrange a set of charged particles in such a way that a region of stable containment for an electron is established. This requires the existence of a point in empty space such that the force vector everywhere on the surface of an incremental region surrounding that point is directed inward. But according to Gauss's law, the integral of the force vector over any closed surface equals the charge contained within the surface. Thus the integral of the force over any closed surface in empty space is zero, which implies that if it points inward on some parts of the surface, it must point outward on other parts, so it is clearly not a stable equilibrium point. The best we could do is have a force of zero over the entire surface, but this too is not stable, because there is no restorative force to oppose any perturbations. According to Gauss' law, the only point that could possibly be a stable equilibrium point for an electron is a point where a positive charge resides, e.g., a proton. Classically an electron would be expected to collapse onto a proton, assuming it had no angular momentum. In the presence of angular momentum, it's possible to have (idealized) stable orbits in the context of Newtonian gravitation, because Newton's gravity did not radiate energy when charges (i.e., masses) are accelerated. However, electric charges were known classically to radiate energy, so even naive orbital models were ruled out. This made it clear that some other principles must be invoked to account for stable configurations of electrically charged matter. (In general relativity, simple two-body orbital systems also radiate energy, in the form of gravitational waves, so the same argument can ultimately be against the possibility of stable configurations for inertially charged matter as well, although in this case the rate of energy radiation is so low that the configurations are essentially stable for practical purposes.)
Incidentally, if we don't require a static configuration, then it is possible to achieve quasi-stable levitation with permanent magnets by spinning the levitated object and using the gyroscopic moments to offset the instability. A number of interesting devices of this type have been constructed. This form of levitation is called quasi-stable (rather than stable) because the rotation of the levitating object results in the emission of energy in the form of electromagnetic waves, so eventually the rotation will be brought to a stop, and then the system will go unstable.