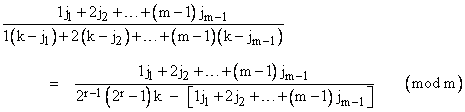Whole Permutation Fractions

For my part, if a lie may do thee grace,

I’ll guild it with the happiest terms I have.

Using each of the decimal numerals 1 through 9 exactly once, we can construct a fraction equal to 3 in two different ways, namely, 17496/5832 and 17469/5823. We say that 3 can be expressed as a whole permutation fraction in the base 10. More generally, for any positive integer b, we say that the integer n is a whole permutation fraction in the base b of degree d if n can be expressed in d distinct ways as the ratio of two integers whose combined digits are precisely the non-zero numerals in the base b. Clearly the number of permutation fractions for any given base is finite, since there are only a finite number of permutations of the b-1 non-zero numerals, and b-2 positions in which to place the division symbol. Of these (b-2)[(b-1)!] fractions, only a subset are whole numbers, and of course there are whole numbers with more than one representation.

For example, the non-zero numerals in the base 4 are {1,2,3}, and the whole permutation fractions in the base 4 are

where the subscript “4” signifies that the expression is to be interpreted in the base 4. (Unsubscripted numbers are understood to be in the base 10.) Each of these numbers is of degree 1, because they each have just one representation.  All 14 of the whole permutation fractions in the base 5 are also of degree 1. The first example of a whole number with more than one representation is in the base 6, where we have

In larger bases we find some numbers have many representations, whereas most have few or none. In the base 7, the number 2 has five distinct representations

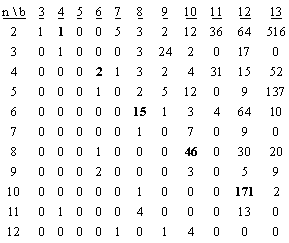
whereas the number 3 has none at all. The table below lists the number of permuted fractional representations for the first several integers in the bases from 3 to 13.

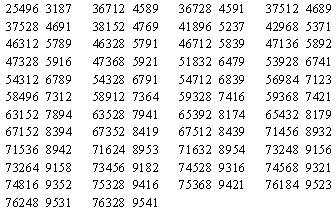
We might not have expected to find such erratic variations in the degrees of numbers for a given base. Why, for example, are there as many as 46 representations of the number 8 in the base 10? Here are the numerators and denominators for these 46 fractions, each of which is equal to 8:

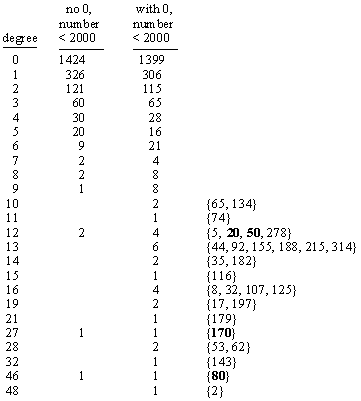
Thus the number 8 is of degree 46 in the base 10. To give an idea of how unusual this is, the following is a list of how many of the numbers from 1 to 2000 are of degree 0, 1, 2, and so on.

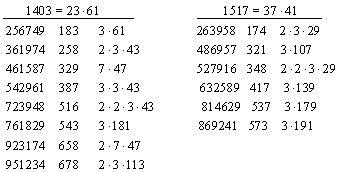
Other numbers that stand out, due to their size and large numbers of representations, are 1403 and 1517, which might be called the Shrewsbury Number and the Wittenberg Number respectively. The numerators and denominators of the permutation fractions for these numbers in the base 10 are listed below, along with the factorizations of their denominators.

Of course, it’s also clear that no multiple of the base b itself can be representable in the base b, because this would imply that the least significant digit of the numerator was zero, which we have excluded from the permuted numerals. (It also appears that no number exceeding a multiple of b by 1 can be represented.) If we allow the numeral zero, the distribution of degrees is actually fairly similar to the distribution without the zero numeral, except that there are a few more examples of high-degree numbers, as summarized in the table below.

The 46 representations of 80 are identical to the representations of 8, except that each numerator is multiplied by 10.  Likewise the 27 representations of 170 and the 12 representations of 20 and 50 are based on the “no zero” representations of 17, 2, and 5. It’s also worth noting that the number 8 has 16 essentially new representations when we allow the zero numeral. These are summarized below.

Each of the 46 representations of 8 without the zero numeral can be converted to a representation with a zero numeral in one of two ways, by appending the 0 numeral as the most significant digit of either the numerator or the denominator. Hence, the total number of distinct representations of 8, including all ten numerals in the base 10, is 2(46)+16 = 108.

The last of the 16 fractions listed above is interesting for having the digits appearing consecutively, i.e., the denominator is 12345 and the numerator is 98760. A similar pattern can be seen in other even bases. For example, in the base 8, the ratio of (7650)₈ divided by (1234)₈ is 6, and the number 6 is of unusually high degree in the base 8. Perhaps the most striking difference between the cases with and without zero is that the number 2 has 48 representations with zero, compared to only 12 representations without zero.

One reason for excluding zero is that it renders some of the solutions indeterminate. Every representation without zero can also be expressed as a representation with zero by appending zero as the most significant digit of either the numerator or the denominator – but not both. The presence or absence of a leading zero has no significance, and yet it makes the difference between a valid and invalid representation. So there is some justification for excluding the zero numeral.

Returning to the no-zero representations, the previous table for bases 2 to 13 suggests that if b is of the form 4k-1 then no odd number is representable in that base. This is easily proven, because in this case the set of numerals, 1 to b-1, contains an odd numbers of 1’s modulo 2, which must be placed in either the numerator or denominator. Of course, the base itself equals 1 modulo 2, so the parities of the numerator and denominator simply equal the parities of the sum of their digits. Consequently either the numerator or the denominator is even and the other is odd. If the numerator is even and the denominator odd, then the ratio is even, whereas in the reverse case the ratio is not an integer. Hence no odd number is representable for bases of the form 4k-1.

On the other hand, if the base b is of the form mk + 1 where k is an odd integer and m = 2^r with r greater than 1, then the residues modulo m of the numerals consist of k multiples of the set {0, 1, 2, 3, …, m-1}, so the numerator and denominator modulo m can be written in the form

or the reciprocal of this. Noting that 2^r – 1 = -1 modulo m, and that 2^r-1 = -2^r-1 modulo 2^r, the numerator can be any of the residues 0, 1, 2,…, (m-1) leading to the m possibilities (or 2m, counting the reciprocals)

The first of these represents possible whole fractions congruent to even residues modulo 2^r. The rest represent the other possible whole fractions. Reducing these (where possible) so that both the numerator and denominator are odd, and hence co-prime to m, the divisions are unique modulo m, allowing us to determine the possible odd residue classes. To illustrate, consider the base b = 13, which can be expressed as b = 2²3+1, so m = 4, k = 3, and the possible odd residue classes are

The central expression doesn’t reduce to an odd whole residue, but the others reduce to 1 (mod 4). Hence, the possible residue classes for numbers expressible as whole permutation fractions in the base 13 are 0, 1, and 2 (mod 4), so no number congruent to 3 (mod 4) is representable, which agrees with the previous tabular results.

For another example, consider the base b = 17, which can be expressed as b = 2⁴+1. In this case we have m = 16 and k = 1, so in addition to the even numbers we can determine the possible odd residue classes by evaluating the ratios j/(8-j) modulo 16 for j = 1 to 15. However, since j/(8-j) = (16-j)/(8-(16-j)), we need only consider j = 1 to 7, i.e., the ratios

Evaluating these fractions modulo 16, we get 7, 11, 7, 1, 7, 3, and 7 respectively. Hence the possible odd residue classes modulo 16 for numbers expressible as whole permutation fractions in the base 17 are 1, 3, 7, and 11, which implies that numbers congruent to 5, 9, 13, and 15 cannot be so expressed.

This approach seems to allow us to determine not only the possibility, but also the frequency with which numbers of various residue classes can be represented as whole permutation fractions of a given base. For example, with the base b = 11 the sum of degrees of the numbers less than 500 in each residue class modulo 10 are 56, 0, 95, 0, 267, 0, 55, 0, 56, and 0. Thus there is a pronounced preference for numbers congruent to 4 modulo 10. We might conjecture that these numbers for the odd residues are in proportion to 3, 5, 14, 3, 3. For another example, in the base b = 17, assuming each possible value of j is equally likely, we would expect the residue class 7 to be three times more populated than the classes 1, 3, and 11.

Return to MathPages Main Menu