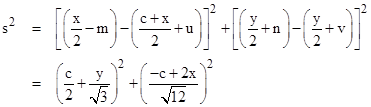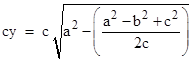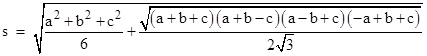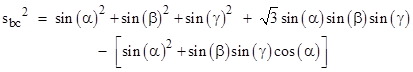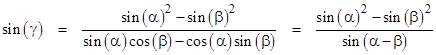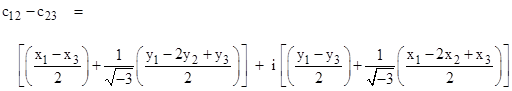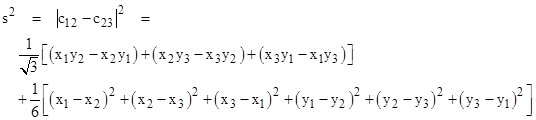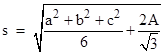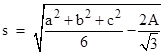Napoleon's Theorem

We expect all things from you, General, except a lesson in geometry.

                                                                                Laplace, 1797

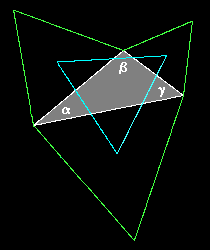
Napoleon's theorem states that if we construct equilateral triangles on the sides of any triangle (all outward or all inward), the centers of those equilateral triangles themselves form an equilateral triangle, as illustrated below.

This is said to be one of the most-often rediscovered results in mathematics. The earliest known appearance of this theorem is as a challenge problem posed by William Rutherford in "The Ladies Diary" in 1825 (four years after Napoleon Bonaparte died on St Helena). Rutherford was probably not the first discoverer, but there seems to be no direct contemporary evidence supporting any connection with Napoleon, although we know the latter actually did discuss geometrical problems with several well known mathematicians. Already as a boy, Napoleon showed a talent for mathematics. According to Markham's biography,

To his teachers Napoleon certainly appeared a model and promising pupil, especially in mathematics... The school inspector reported that Napoleon's aptitude for mathematics would make him suitable for the navy, but eventually it was decided that he should try for the artillery, where advancement by merit and mathematical skill was much more open...

Even after becoming First Consul he was proud of his membership in the Institute de France (the leading scientific society of France), and was close friends with several mathematicians and scientists, including Fourier, Monge, Laplace, Chaptal, Berthollet, and Lagrange. (Oddly enough, Markham refers to Fourier as Francois, apparently confusing him with the social reformer and utopianist. The mathematician and friend of Napoleon was actually Jean Baptiste Joseph Fourier, no relation to Francois as far as I know, although they were almost exact contemporaries.) Indeed, in his grand expedition to Egypt in 1798 Napoleon brought along (in addition to 35,000 troops) over 150 experts in various fields, among them Monge, Fourier, and Berthollet, not to mention a complete encyclopedie vivante with libraries and instruments. Napoleon held long discussions with his movable Institute - much to the consternation of his generals, who had trouble staying awake during these sessions.

One result of the expedition was that Fourier served for a time as the governor of lower Egypt. Likewise Laplace (who interviewed the young Napoleon for admission to the artillery) received titles and high office as a result of his friendship with Bonaparte, as did Lagrange. However, Laplace was relieved of his duties as the Minister of the Interior after only six weeks, and Napoleon later commented that Laplace had "sought subtleties everywhere, had only doubtful ideas, and carried the spirit of the infinitely small into administration". The most famous exchange between these two men occurred after Laplace had given Napoleon a copy of his great work, the Mecanique Celeste. Napoleon looked it over, and remarked that in this massive volume about the universe there was not a single mention of God, its creator. Laplace replied "Sire, I had no need of that hypothesis".

According to Wetzel, the earliest known attribution of the theorem to Napoleon is a parenthetical comment, “Theorem proposed for demonstration by Napoleon to Lagrange”, in an Italian textbook of elementary geometry by A. Faifofer published in 1911. This accords with Harris’ comment that “after the revolution, [Lagrange] fell into the favor of Napoleon Bonaparte, who enjoyed sharing geometrical puzzles with Lagrange and Laplace”. Indeed we know that Napoleon discussed the problem of quadri-secting a circle with his mathematician friends. Despite this, Coxeter and Greitzer claimed that

The possibility of [Napoleon] knowing enough geometry for this feat is as questionable as the possibility of his knowing enough English to compose the famous palindrome, ABLE WAS I ERE I SAW ELBA.

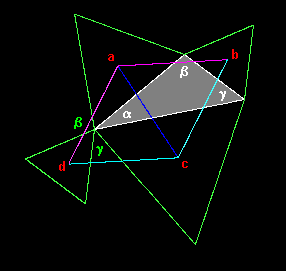
The basis for the dismissive claim is unclear, especially since the theorem has been discovered by many amateurs. Despite the late date and unknown source of Faifofer’s remark, it isn’t inconceivable that Napoleon could have found the theorem, or at least that the proposition could have been among the “geometrical puzzles” mentioned in communications between Napoleon and Lagrange. The theorem is also quite easy to prove. Consider the drawing below, where the original triangle is shaded in gray, and we have added a 4th equilateral triangle to the left hand vertex.

Notice that if we rotate the figure counter-clockwise through an angle of 2π/3 about the point "c", the triangle originally centered at "b" moves to the position originally occupied by the triangle centered at "d". Thus the line segments cb and cd are of equal length and make an angle of 2π/3. Likewise if we rotate the figure clockwise through an angle 2π/3 about the point "a", the triangle centered at "b" again moves to the position of the triangle at "d", so the line segments ab and ad are of equal length and make an angle of 2π/3. Consequently the line ac bisects the angles at "a" and "c", so the triangle abc has an angle of π/3 at each vertex, so it is equilateral (as is acd). This completes the proof, which is simple enough that it could easily be found by a bright school boy.

In any case, the theorem really just expresses the nice tiling pattern, as shown below:

This makes the theorem visually obvious, and is also suggestive of various generalizations, but it doesn't provide much quantitative information. Given the edge lengths A,B,C of the original triangle, what is the edge length of "Napoleon's equilateral triangle"? It's not too difficult to give a proof of Napoleon's theorem using coordinate geometry and a little algebra that also yields the answer to this question. It turns out to be closely related to Heron's formula for the area of a triangle in terms of the edge lengths.

If we construct equilateral triangles on any two of the sides of the given triangle, the distance from their centers is the same, regardless of which two sides we choose. Hence, if we express this distance in terms of the edge lengths, it must be a symmetrical function of those lengths, i.e., any permutation of the edges should leave the result unchanged. The same is true for the area of a triangle, so we shouldn't be surprised if there turns out to be a relation between the sides of Napoleon's equilateral triangle and the area of the original triangle. On the other hand, these two quantities can't be identical, nor even proportional, because we can have a degenerate triangle with zero area but still a non-zero edge length for Napoleon's equilateral triangle.

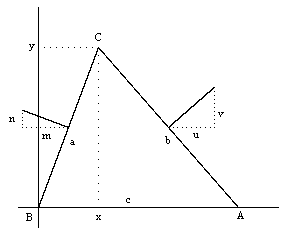
To give another proof Napoleon's theorem, and in the process discover how to express the sides of the Napoleon's triangle in terms of the sides of the given triangle, consider the general case of a triangle with edge lengths a,b,c placed on a Cartesian coordinate system with the side c on the X axis as shown below.

The center of the equilateral triangle constructed on the side a is to be found by moving from the midpoint of that side perpendicularly outward a distance of a/(12)^1/2. The components m,n of this segment satisfy the requirements

where x,y are the coordinates of the vertex opposite the side c. Thus, noting that x² + y² = a², we find

Likewise we can find the components for the segment leading from the midpoint of the side b to the center of the equilateral triangle constructed on b. Making use of x = (a² - b² + c²)/(2c) we have

In terms of these lengths the distance s between the centers of the equilateral triangles constructed on the edges a and b can be expressed as

Expanding the squares gives

Noting that the last term is x²/3, we can combine this with y²/3 to give a²/3. Also, we can combine c²/4 and c²/12 to give c²/3. Furthermore, recalling that 2cx = a² - b² + c², we can make this substitution and collect terms to give

Now, since y² = a² - x², the quantity cy can be written as

This is just twice the area of the triangle with sides a,b,c, as discussed in the note Heron's Formula For Triangle Area, and it has the symmetrical factorization

Hence the distance between the centers of the equilateral triangles constructed on the sides a and b is

Since this is perfectly symmetrical in the three sides, it's clear that the distances between the centers of the equilateral triangles constructed on any two sides of the triangle are the same, and so the triangle formed by connecting those centers is equilateral, which proves Napoleon's theorem. The theorem can be generalized to say that the centers of regular n-gons constructed on the sides of a regular n-gon form a regular n-gon, and naturally it also applies to n-gons subjected to conformal and affine transformations.

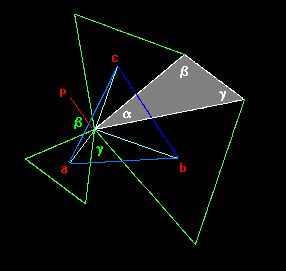
Another proof of Napoleon's Theorem, based on a more explicit trigonometric approach, can be developed from the figure below.

Recall that the edge lengths of a triangle are proportional to the sines of the opposite angles, which implies that the lengths of the segments from the vertex to the centroid of the equilateral triangles centered on points a,b,c are proportional to sin(α), sin(β), sin(γ) respectively. Therefore, noting that the angle between the segments Pb and Pc is α + π/3, the normalized squared length of segment can be expressed using the law of cosines as

Adding and subtracting sin(α)² and expanding the cosine of α + π/3 in the above expression gives

Napoleon's Theorem is true if and only if the corresponding expressions for the squares of the other two normalized lengths s_ab and s_ca equal this same value. These expressions are given by simply permuting the angles α, β, and γ. Since the overall expression is obviously symmetrical under transpositions of β and γ, and the first four terms are symmetrical in all three of the angles, it only remains to consider the effect of transposing α and β on the quantity in the square brackets. Hence Napoleon's Theorem is equivalent to the equality

Solving for sin(γ) gives

Since α, β, and γ are the three interior angles of a triangle, we have γ = π - (α + β), and therefore sin(γ) = sin(α + β). Making this substitution, the above relation is equivalent to the trigonometric identity

We can write this in a more familiar form by making the substitutions sin(x)² = (1-cos(2x))/2 on the right hand side, and defining u = α - β and v = α + β. This gives

This identity is easily verified by writing the sines and cosines in exponential form, and carrying out the multiplications.

Yet another approach to Napoleon's Theorem is by representing points in the plane as complex numbers. Both the premise and the conclusion of the theorem involve equilateral triangles, so it will be useful to know the necessary and sufficient on three complex numbers z₁, z₂, z₃ to be the vertices of an equilateral triangle. The centroid of these points is simply z₀ = (z₁ + z₂ + z₃)/3, and the rays from the centroid to the vertices are (z₁ - z₀), (z₂ - z₀), and (z₃ - z₀). The vertices form an equilateral triangle if and only if these rays are of equal length L and separated by the angle 2π/3. Hence the necessary and sufficient condition is

for some arbitrary angle θ. It follows that

Substituting for z₀ and expanding the products, we arrive at the condition

This condition on the vertices of an equilateral triangle can be expressed in several alternate (but algebraically equivalent) forms, the most fundamental of which is

Another equivalent form is

Also, since the quantity in the left parentheses is 3z₀, this can be written as

which represents an alternate expression for the centroid of an equilateral triangle.

Given any two points, these expressions enable us to compute a third point that forms an equilateral triangle with the first two. Of course, the relation is quadratic in each of the three points, so there are two solutions, corresponding to the two possible directions that the third point can lie in with respect to the other two. Given z₁ and z₂, an equilateral triangle is formed by setting z₃ to either of the values

Therefore the centroid of this triangle is at

The root given by the + sign places the centroid such that the loop 1,2,0 proceeds in the counter-clockwise direction. Now, if we are given three arbitrary points p₁, p₂, p₃ in the complex plane, Napoleon's Theorem asserts that the centroids of the outer equilateral triangles on the bases (p₁,p₂), (p₁,p₃), and (p₂,p₃) form an equilateral triangle. Letting c₁₂, c₁₃, and c₂₃ denote these centroids, we can use the preceding formula to express these in terms of the points p₁, p₂, p₃. For example, we have

It is then straightforward to verify that

so the centroids do indeed satisfy the condition for being the vertices of an equilateral triangle. Furthermore, letting p₀ denote the centroid of the original triangle (not necessarily equilateral), the right-hand quantity is 3p₀², but we know that the middle quantity equals 3c₀² where c₀ is the centroid of the equilateral triangle formed by the three original centroids. Consequently, the centroid of Napoleon's triangle coincides with the centroid of the original three points.

We can also verify the expression for the length of the edge of Napoleon's triangle given above. The length is simply |c₁₂ - c₂₃|, i.e., the magnitude (norm) of the difference between two vertices. We have

Letting p₁ = x₁ + i y₁, etc., this becomes

The squared length of the edge is then the product of this quantity and its complex conjugate, so we have

The quantity in the first square bracket is just twice the area of the original triangle (as discussed in Net Area and Green's Theorem), and the quantity in the second square bracket is the sum of the squares of the edge lengths of the original triangle. Hence if we let A denote the area and a,b,c denote the edge lengths of the original triangle, the edge length of Napoleon's triangle is

in agreement with the previous demonstration.

Incidentally, we based the above discussion on equilateral triangles formed on the exterior of a three sides of a triangle, but we could just as well consider equilateral triangles formed on the interior of the three sides of a triangle. We find (again) that the centroids of the three equilateral triangles are the vertices of an equilateral triangle, but for this interior version of Napoleon’s theorem the edge length is

Since the area of an equilateral triangle with edge length s is s²(√3)/4, it follows that

where A_ext and A_int are the areas of the Napoleonic external and internal equilateral triangles respectively, and A is the area of the original triangle.

Return to MathPages Main Menu