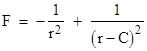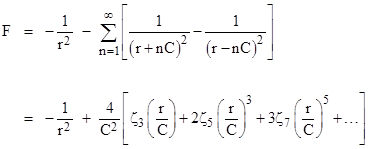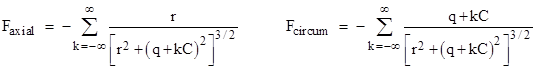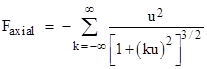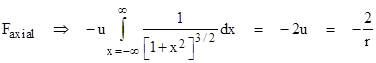Newtonian Gravity In Closed or Curved Space

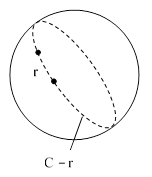
A classical force-at-a-distance theory, such as Newtonian gravity, is problematic if the "distance" between two particles is not unique. For example, consider two particles in a spherical universe of circumference C, and define a distance between those two particles as the metric length of a geodesic path between them. If the particles are separated by a minimum distance r, then they are also separated by a distance C − r in the opposite direction, as shown below.

So, naive application of the inverse square formula for these two geodesic distances would give

But this isn't complete, because the particles are also separated by the geodesic distances r + 2C, r + 3C, etc., and in the opposite direction by r − 2C, r – 3C, and so on. This leads to the infinite series

where ζ_n is the zeta function, defined as

If the circumference C of the universe is sufficiently large, this would be almost exactly an inverse-square force for small distances r, but for distances comparable to C the force law would include terms proportional to r, and then r³, and so on.  Coincidentally, the cosmological constant term in general relativity leads to a small force of repulsion proportional to r, just as we get from a naïve application of the inverse-square formula for the geodesic distances in a spherically closed universe.

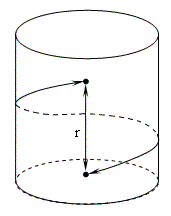
We could also consider an inverse-square force law in a flat space with a cylindrical dimension. Consider two points on a cylinder of circumference C, as shown below.

If the two particles are at the same angular position but separated by an axial distance of r, then the points are obviously separated by a geodesic of length r, but they are also separated by a geodesic whose squared length is r² + C² that loops once around the cylinder. In fact, they are separated by infinitely many geodesics of squared lengths r² + nC² for n = 0, 1, 2,..., where n denotes the number of loops around the cylindrical dimension. Of course, for each of these spiral paths in the clockwise direction there is one of identical length in the counter-clockwise direction, so the circumferential components of the corresponding force terms would cancel, leaving only the axial components. However, this is true only because the two particles are circumferentially aligned. In general, if the particles are separated by an axial distance r and a circumferential distance q, the axial and circumferential forces would be given by the infinite series

Since the circumferential distance q appears only in the quantity q + kC, and the summations are taken over all integers k, it follows that we can use any value of q modulo C. If we imagine a universe with one or more curled-up dimension(s), and forces with components to the inverse-square of the length of each geodesic path between two particles, we would arrive at force laws of this kind. For values of r greater than C, the axial force approaches −2/r, so it would not give an apparent inverse-square force. To prove this for q = 0, we can define the variable u = 1/r and set C = 1, so the axial force is given by the summation

For large r, the value of u is very small, so the quantity ku varies almost continuously as k increments through the integers. Therefore, the summation over k approaches an integral over the quantity x = ku. Noting that dk = (1/u)dx this gives

Similar considerations apply in the context of classical electromagnetism, according to which the potential at any given event is the sum of the contributions of all the charge on the past light cone of that event. In a closed cylindrical space (for example) the past light cone of each event intersects with each charge infinitely many times.

It’s also interesting to consider Gauss’ law in a flat closed space, such as a space that is cylindrical in all dimensions. According to the usual interpretation of Gauss’ law, the integral of the normal flux over any closed surface is proportional to the net “charge” enclosed within the surface. However, if the space itself is closed, then each closed surface within the space can be regarded as “enclosing” two regions. In the case of electric charge we can rationalize this by positing that the universe contains an equal amount of positive and negative charge, so that a small closed surface with nothing “inside” it will have zero flux on its surface, consistent with the fact that the net charge enclosed “outside” the surface is also zero. On the other hand, the force of gravity seems to be more difficult to rationalize in this context, because it suggests that the flux over a small closed surface, enclosing nothing but empty space in its “interior”, must be proportional to the total amount of mass in the universe. Moreover, the smaller the surface, the higher the flux density, so the density would approach infinity as the surface shrinks to a point.

It’s interesting to compare this with Maxwell’s discussion of the viability of electromagnetic and gravitational theories based on the actions of an all-pervasive medium (in his paper on A Dynamical Theory of the Electromagnetic Field):

Gravitation differs from magnetism and electricity in this; that the bodies concerned are all of the same kind, instead of being of opposite signs… and that the force between these bodies is an attraction not a repulsion… The intrinsic energy of the field of gravitation must therefore be less wherever there is a resultant gravitating force…Hence those parts of space in which there is no resultant force… must have an intrinsic energy per unit volume greater than R²/(8p) where R is the greatest possible value of the intensity of gravitating force in any part of the universe.

He bases this on the proposition that energy is essentially positive, so “it is impossible for any part of space to have negative energy”. Oddly enough, the usual convention today is to regard the potential energy of a particle in a gravitational field as zero when infinitely distant from the source, and progressively more negative as it approaches the source. This is not regarded as especially problematic, but it was unacceptable to Maxwell, who concluded by saying

The assumption, therefore, that gravitation arises from the action of the surrounding medium in the way pointed out, leads to the conclusion that every part of this medium possesses, when undisturbed, an enormous intrinsic energy, and that the presence of dense bodies influences the medium so as to diminish this energy wherever there is a resultant attraction. As I am unable to understand in what way a medium can possess such properties, I cannot go any further in this direction in searching for the cause of gravitation.

If we consider not just closure but internal curvature, it becomes questionable whether Gauss’ law is still applicable, especially in a theory of gravitation (like general relativity) in which gravitation itself has gravity. According to the Faraday-Maxwell conception, lines of force can only terminate in “charges”, not in empty space, but according to general relativity space can be considered as, in a sense, charge. Curvature also affects how rapidly the lines of force diverge as a function of distance, and the surface area of a sphere (for example) has no fixed relationship to the radial “distance” from the center, so the correspondence between force at a distance and Gauss’ law breaks down.

Return to MathPages Main Menu