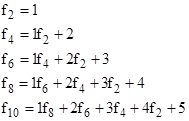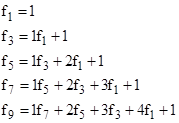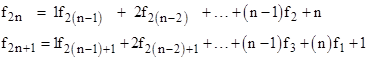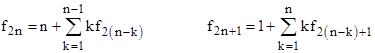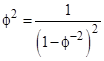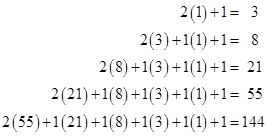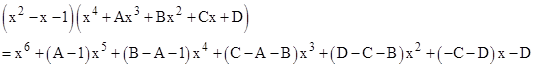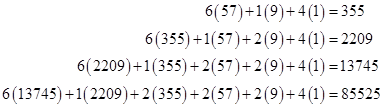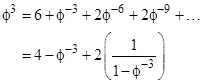Interleaving Fibonacci Numbers

The sequence of Fibonacci numbers is defined by the initial values f₀ = 0, f₁ = 1, and the recurrence f_n = f_n-1 + f_n-2. The first several values are

Notice that the even-ordered terms satisfy the relations

and so on. Similarly the odd-ordered terms satisfy the relations

and so on. One way of proving that this pattern continues is by induction. We know by inspection up to a certain n that consecutive Fibonacci numbers are given by

(Note that this requires f₁ = f₂ = 1.) Adding these together, term by term, it follows from the basic Fibonacci recurrence that the next even-ordered value in the sequence is

which is of the same form as the previous even-ordered term, but with n+1 in place of n. Likewise the next odd-ordered value in the sequence can be found by adding this expression for f_2(n+1) to the preceding expressing for f_2n+1, which gives

where we have used the fact that f₁ = 1. This is of the same form as the previous odd-ordered term, but with n+1 in place of n, so the induction is complete. There, the interleaving odd and even parts of the Fibonacci numbers satisfy the relations

Naturally these identities are closely related to the generating functions for the recurrence relations. We know the ratios of successive values of fn asymptotically approach successive powers of the dominant root ϕ of the characteristic equation x² – x – 1 = 0. Therefore, with n = 6, the even-ordered relation approaches

and if we divide this by ϕ¹⁰ we get

Taking this to the limit as n goes to infinity, and substituting for the derivative of the geometric series, we get

which is equivalent to the characteristic equation ϕ² – ϕ – 1 = 0. However, this isn’t the only possible expansion of the terms of the even (or odd) ordered Fibonacci sequences. For example, given the even-ordered sequence 0, 1, 3, 8, 21, 55, 144, … we could simply apply the “greedy algorithm” by expressing each term as the sum of the maximum number of the immediately preceding terms. Thus we have

From this it’s easy to see that f_2n = f_2(n-1) – f_2(n-2) + 2f_2(n-1), so the even-ordered Fibonacci numbers satisfy the recurrence

which has the characteristic equation

This shows that another way of arriving at the recurrence for the kth Fibonacci numbers is to solve for the (k–2)th degree polynomial that gives, when multiplied by the characteristic polynomial of the Fibonacci sequence, a polynomial whose only non-zero coefficients are for powers that are multiples of k. For example, to find the recurrence for every third Fibonacci number, we evaluate the product

We need the coefficients of x⁵, x⁴, x², and x to vanish, so we require A = 1, B = 2, C = –1, and D = 1. Hence the characteristic polynomial for every third Fibonacci number is

with the corresponding recurrence relation

Naturally the same type of relations can be derived for any linear recurring sequence. For example, consider the “tribonacci” sequence, defined by the initial values t₀ = t₁ = t₂ = 1, and the recurrence t_n = t_n-1 + t_n-2 + t_n-3. The first several values are shown below.

To find the recurrence formula for every third term of this sequence, we can apply the greedy algorithm to express the terms 1, 9, 57, 355, 2209, 13745, 85525, … as follows

From this it’s easy to see that t_3n = t_3(n-1) – 5t_3(n-2) + t_3(n-3) + 6t_3(n-1), so we have the recurrence

corresponding to the characteristic polynomial

We can relate this back to the greedy recurrence by examining the asymptotic expression in terms of the dominant root ϕ, which can be written in the form

This implies that f is a root of the characteristic polynomial, as expected. Incidentally, the “poles” of this recurrence are 0 and the cube roots of 1.

Return to MathPages Main Menu