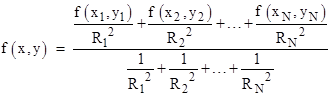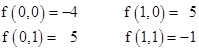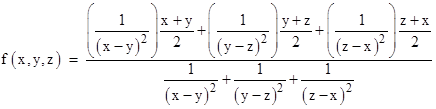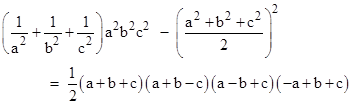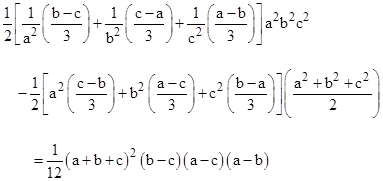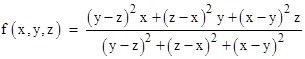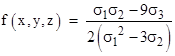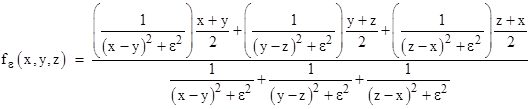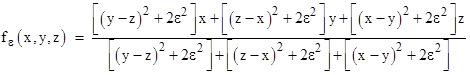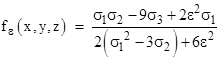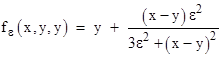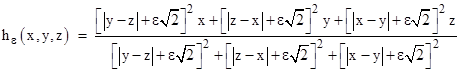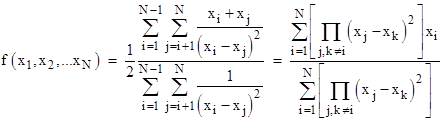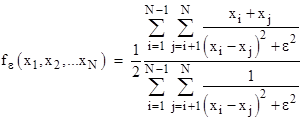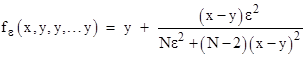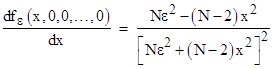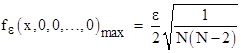Inverse Square Weighted Interpolation

Suppose we wish to interpolate a surface through a set of non-uniformly distributed control points z = z(x, y). Of course, there are infinitely many surfaces passing through any finite set of control points, so the result is not uniquely determined unless we specify some additional information, which serves as a criterion for "goodness of fit", constraining the overall shape of the surface.

One common technique is multiple linear regression. This requires us to specify the "form" of the surface. For example, we could specify

and then use linear regression to determine the coefficients A,B,..,G such that the sum of squares of the z errors at the control points is minimized. To ensure that this surface actually passes through each of the N control points, we would need to choose a "form" with N terms. For example, the above form will fit any seven control points exactly.

Another interesting method, and one that automatically passes through each control point, is the "inverse square weighting" method. Given the values of f(x_i,y_i) for N points (x₁,y₁), (x₂,y₂), ... (x_N,y_N), the interpolated function for every other point (x,y) is

where R_i² = (x−x_i)² + (y−y_i)². This can obviously be extended to any number of dimensions. For points (x,y) far from any of the control points, the value of f approaches the average of the f values for the control points.

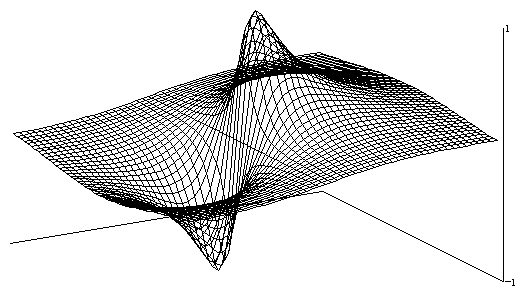
To illustrate, suppose we are given two control points f(0,0) = 1 and f(1,0) = −1. The surface generated by these two points is shown below.

For another example, suppose we are given the four points

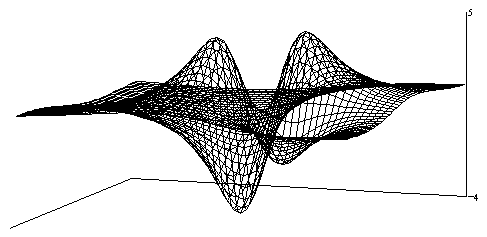
The surface generated by these four points is shown below.

Another possible application of this kind of interpolation involves computing a suitable “average” of multiple signals, each of which could be subject to undetected errors. If we have just two sources, x and y, then clearly there is no basis for inferring that the true mean of the population from which those values were drawn is anything other than (x+y)/2, but suppose we have three values, x, y, and z. In this case we might take the weighted average of the three pairwise averages, with an inverse-square weighting based on the difference between the elements of the respective pair. Thus we could form the value

We can clear the fractions in the numerator and denominator by multiplying through by the product of the square differences. If we let a,b,c denote (x−y), (y−z), (z−x) respectively, the product for the denominator can be inferred from Heron’s identity

Since a+b+c = 0, the right side vanishes, so the left side gives us a useful expression for the denominator after clearing the fractions. To evaluate the numerator of f(x,y,z) after multiplying by the product of squared differences, note that if we add μ to each of the variables x,y,z we would just increase f by μ, so it suffices to evaluate the case with x+y+z = 0. (We confirm later that this covers all cases.) With this condition we have

so we have

With this we can write the numerator multiplied by the squared differences in terms of a,b,c, and then note the interesting identity

Again, since a+b+c = 0, we can equate the two terms on the left side. Consequently, after clearing fractions, we have

(As an aside, we note the remarkable fact that if we replace the squares with fourth powers in this expression, the resulting function is identical; this equivalence does not hold for any other pair of exponents; also the inverse-square function is not equal to the inverse-fourth-power function.) Again, adding any constant μ to each of the variables simply increases f by μ, so this confirms that the equality with the previous expression applies to f(x+μ,y+μ,z+μ) for any μ. This can also be written in the form

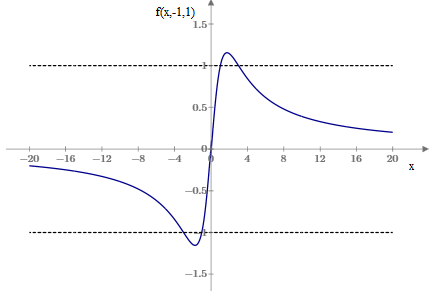
in terms of the symmetric functions σ₁ = x+y+z, σ₂ = xy+yz+zx, and σ₃ = xyz. To visualize the result, consider the case with y = −1 and z = 1 shown in the plot below.

Thus when x is relatively far from the other two, the function approaches the average of the other two. As x passes between those two, the function essentially selects x. This is a well-behaved function, but a practical difficulty arises in the case near the condition x = y = z, which is the only case in which the denominator (i.e., the sum of squares of the differences) vanishes. If just two of the variables, say, y and z, we have f(x,y,y) = y(x−y)²/(x−y)², so the singularity at x=y is removable, but this nevertheless presents numerical precision issues for practical computations.

To eliminate the possibility of the denominator vanishing, we could add a small cutoff term ε² to each squared difference in the inverse-square formulation as follows

The constant ε has the same units as the variables. Clearing the fractions again, this is equivalent to

In terms of the symmetric functions of the variables this can be written as

A non-zero value of ε serves to block the numerical singularity in each inverse-square term if the difference between the variables is zero. Recall that the f function gives f(x,y,y) = y, meaning that if any two of the variables are exactly equal to each other, the function gives infinite weight to those values and disregards the third. In contrast, with non-zero ε we have

so the third value is not completely disregarded when two of the values are equal to each other.

A slightly different approach, that can be found in the literature, is to make use of the absolute value function, and define the selection formula as

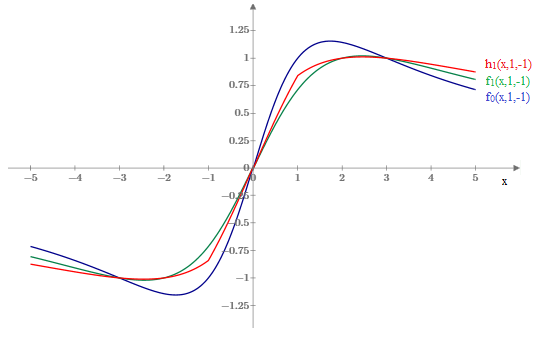
Expanding the squares, we see this is identical to the previous formula, except that it includes cross-products such as 2|x−y|√ε in the weight factors. A comparison of these functions with ε = 1 (along with the original function f₀) is shown below.

Oddly, this latter formula is often presented in the literature with ε√2 replaced with the seemingly dimensionless 1. For example, if x,y,z are three temperatures in units of degrees Celsius, then ε√2 would tacitly corresponds to 1 degree Celsius, whereas if the units of x,y,z were changes to Fahrenheit the implicit value of ε√2 would be 1 degree Fahrenheit, yielding different results. Also the slope of h(x,y,z) has discontinuous slope due to its use of the absolute value function.

Returning to the basic inverse-square formula, it can immediately be extended to N variables x₁, x₂, x₃, …, x_N by considering each of the N(N−1)/2 pairs as follows

where “j,k≠i” signifies that the product is taken over every pair of distinct j,k not equal to i. We can also apply an epsilon cutoff in the inverse square formulation to give

For N > 3 this doesn’t give a simple alternate form. To account for validities, each variable x_i could be assigned a validity q_i equal to either 1 (valid) or 0 (invalid), and each of the pairwise terms in the summations would be multiplied by q_iq_j.

This method is conceptually related to the so-called inverse-variance interpolation method applied to the pair-wise averages of the signals, noting that the mean of each pair is (x_i + x_j)/2 and the variance is (1/2)(x_i – x_j)². Of course, our pairwise averages are not independent, since the same individual signals appear in more than one pair. Also, the ε cutoff provides enhances numerical stability.

For the general case with N inputs, setting all but one equal to y, we have

This shows the idealized behavior if N-1 of the inputs all agree exactly with each other (equalling y), and one input has a different value (x). This gives

Thus the slope at x = 0 is 1/(Nε²), and the function reaches a maximum at x = ε√[N/(N-2)], where it has the value

A discussion of related functions, with exponents greater than 2, see the article on trivariate functions.

Return to MathPages Main Menu