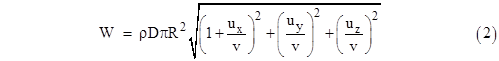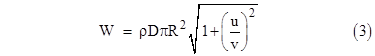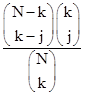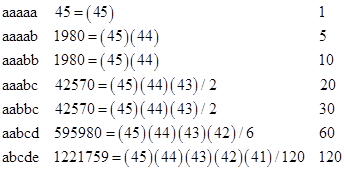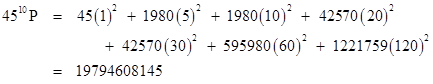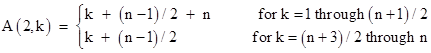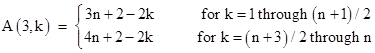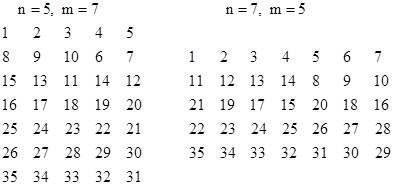Miscellanea

Relative Rain

If someone goes from his house to his car in a rainstorm, will he get more wet, less wet, or equally wet if he runs rather than walks? This is a very commonly asked question. To develop a quantitative answer, let's first consider a spherical man, and assume he moves to his car in a straight horizontal path with velocity v. The raindrops are falling at an angle such that its velocity is u_z in the downward direction, u_x in the horizontal direction (straight into the man's face), and u_y in the sideways horizontal direction (the man's left to right). The intensity of the rain is such that each cubic foot of air contains ρ grams of water.

Relative to the rain's frame of reference the raindrops are stationary and the man and his car both have an upward velocity u_z and a sideways velocity (right to left) of u_y. In addition, the man has a forward horizontal velocity of u_x + v.

Clearly the amount of rain encountered by the man is equal to ρ times the volume of space he sweeps out as he moves relative to this stationary mist of raindrops. Since he is spherical with radius R, this swept volume is essentially equal to πR²L, where L is the distance travelled (relative to the rain's frame of reference).

If D is the horizontal distance to the car, and the man moves straight to his car with velocity v, the time it takes him is D/v. His total velocity relative to the falling rain is

so the distance he moves relative to the rain is L = (D/v)V. Therefore, the amount of rain he encounters in the general case for arbitrary direction of rainfall is

If the rain is falling vertically then u_x = u_y = 0 and the total velocity is u = u_z. In this case equation (2) reduces to

which shows that the key parameter is the ratio of the rain's vertical speed to the man's horizontal speed. Of course, if u was zero (which would mean the rain was motionless relative to the ground), then L would always equal D, regardless of how fast the man runs. On the other hand, for any u greater than zero, the amount of rain he encounters will go down as his horizontal velocity v increases.

We can easily incorporate other assumptions, such as the man having some non-spherical shape. It's just a matter of geometry to compute how much volume he sweeps out relative to the rain's frame of reference. For example, an infinitely thin card could move from house to car at any speed without getting wet at all, provided it is tilted at the aberration angle, so it sweeps out zero volume in the rain's frame.

Two In the Shop

Suppose we have 10 units in service, each with a mean time between failure (MTBF) of 2000 hours. Each operates for 2 months per year. When one fails it is returned to the maintenance shop for repair, and spends 1 week there. What is the probability that two units will be in the maintenance shop at the same time for repair?

Assuming the MTBF is quoted in operational hours, that the failure distribution is exponential, and that the "2 months per year" operational time is spread evenly through the year (e.g., 4 hours per day), it follows that the mean calendar time between failures of a specific unit is 12,000 hours. Also, a unit spends 168 hours (=1 week) in the shop each time it fails. Therefore, each unit has a mean duty cycle of 12168 hours, of which 12000 are spent in the field and 168 are spent in the shop.

The periods in the shop are random and uncorrelated for each of the 10 units. The probability of any particular unit being in the shop at a randomly chosen instant is just p = 168/12168. The probability of two specific units being in the shop at a random instant is p². In general, the probability of exactly k out of 10 units being in the shop at a given instant is

so the probability of finding exactly 2 units in the shop is 0.007675, whereas the probability of two or more in the shop is 0.007970.

Of course, the above analysis also was based on several idealizing assumptions. In reality, the probability could be significantly higher or lower for any of several reasons. For example, the operational periods might not be independent and uniformly distributed over the year, so it's possible that all the units are operational for the same 2-month period each year, which would increase the probability of having two in the shop at some point during the "busy season". On the other hand, the real probability could also be much smaller. Strictly speaking, within the stated conditions of the original problem, the probability of two or more units in the shop at the same time could be anything from 0 to about 0.3874. For example, if each unit operates for exactly 2000 hours between failures, we could stagger their repair cycles so that one fails every 200 hours, which is greater than the one week repair time of 168 hours. Thus, the probability of two in the shop would be 0. (One could also manipulate the probability by assuming the units operate in more or less mutually exclusive 2-month periods during the year.)

On the other hand, if the units are operated in synchronized pairs (hopefully not two engines of a twin-engine airplane), and each fails every 2000 hours exactly, then each pair is in the shop for 168 hours out of every 2168 hours, giving a probability of 0.0774. If the five pairs of units are staggered, then the fraction of [active] time with two units in the shop would be 0.3874.

Anti-Carmichael Pairs

Let the integers a,b be called an "anti-Carmichael pair" if a divides b(b−1) and if b divides a(a−1). This definition was suggested by George Baloglou, who gave the example a=63,b=217. Here's one way of characterizing all such pairs: We want positive integers A,B such that A divides B(B−1), and B divides A(A−1), which implies integers M,N such that

Let c be the greatest common divisor of A and B, so we have A=ac, B=bc where gcd(a,b)=1. The above equations become

Since a and b are coprime we know that a divides M, and b divides N, so there are integers n,m such that M = ma and N = nb. Thus the above equations reduce to ac−1 = mb and bc−1 = na, which can be written as

Since a and b are coprime we are guaranteed infinitely many solutions of each of these equations. The solutions of the left hand equation will be of the form c = c₀ + bk and of the right hand will be c = c₀ + aj, for any integers k and j, and so the simultaneous solutions to both equations are of the form c = c₀ + (ab)t for any integer t. The value of c₀ can be found via the Euclidean Algorithm applied to either of the above equations. (Incidentally, also we have the linear equation a²n − b²m = (b−a).)

The preceding shows that (A,B) = (ac,bc) is an anti-Carmichael pair if and only if

for any non-negative integer t, where c₀ is the least positive solution of ac – bm = 1. Thus for any pair of coprime integers (a,b) we can construct the unique infinite family of anti-Carmichael pairs. For example, let's take a=9 and b=31. The least positive solution of 9c−31m = 1 is with c = 7, so it follows that any pair of integers of the form ( 9(7+279t), 31(7+279t) ) is anti-Carmichael for any non-negative integer t. With t = 0 this gives George's (63,217), whereas with t = 1 it gives (2574,8866), and so on.

A String Algebra

Given a group G of order g, let U denote the set of all ordered multi-sets of elements of G. Elements of U are called "strings", and the number of components in a string q is called the “length" of q. A string consisting only of t repetitions of the identity element of G is signified by I_t and is called a "null string". Let V denote the subset of U consisting of multi-sets with exactly g components, and let A denote the subset of V consisting of multi-sets of exactly g distinct components.

For any string q of length t, and any integer d that divides t, we define the "contraction" C(q,d) as the ordered set of elements of G given by cumulative compositions of the components of q taken in t/n sets of n consecutive components. For example, if q consists of {q₁, q₂, q₃, q₄, q₅, q₆} then C(q,2) is defined as {q₁q₂, q₃q₄, q₅q₆}.

Also for any string q and any integer k we define the "rotation" R(q,k) as the string consisting of the components of q all shifted k places to the left, wrapping the leftmost element to the rightmost place with each shift. Thus, with q as above, the string R(q,2) is given by {q₃, q₄, q₅, q₆, q₁, q₂}.

The "successor" of any string q of length t is defined as the string

We will denote j iterations of the successor function beginning with q as S(q,j).

These strings of group elements have many interesting algebraic possibilities with various operations. For example, given two strings

of length j and k respectively, we can define a string of length k + j by the catenation

and a string of length kj by the compositional "cross product"

If k = j we also have the "interleaving" operation

and the "dot product" defined by

These operations, together with the contraction, rotation, and successor functions defined above, produce an interesting algebraic structure.

Zulu Hitler

During the first world war two generals, Paul Von Hindenburg and Erich Ludendorff, rose to pre-eminence in Germany, and became virtual dictators of the country. Ludendorff first became known in the early days of the war when he commanded the assault on the Belgian fortresses at Liege, capturing the forts within 48 hours. Shortly thereafter Germany was threatened on its eastern borders by huge Russian armies, and Ludendorff was named chief of staff to the elderly Paul von Hindenburg, who was called out of retirement to command the defense. (Hindenburg's first military action was in the Seven Weeks War of 1866.) Under this leadership team (and with the assistance of Colonel Hoffmann) the German army won a spectacular victory at Tannenberg, in which a whole Russian army was encircled and annihilated. The battle was actually centered on another village, Frogenau, but it was given the name of Tannenberg to avenge the medieval loss of the Teutonic knights to the Poles in 1410, thereby enhancing its mythic significance.

Thereafter the prestige of the two generals, Hindenburg and Ludendorff, continued to grow, and by the end of the war this partnership virtually ruled Germany, in both military and civilian matters. (Some insiders slyly referred to Hindenburg as General Was Sagst Du, because whenever he was asked a question he would turn to his chief of staff and say "What says you, Ludendorff?") They worked so closely together that they came to be regarded as, in some sense, almost a single entity, and their edicts were signed simply with the initials HL.

This reminds me of the conventional reference point for longitude on the earth's surface. By international agreement the line of reference is taken to be the line passing through Greenwich, England. This is called Zero Longitude, and every other longitude is referenced to this location. The designation is sometimes abbreviated as ZL, but it has become more common to use the word "Zulu", possibly because a single word with vowels separating the consonants is more memorable or easier to pronounce. It may also be a result of the interesting human tendency to jargonize expressions. (As far as I know, there is no connection between this terminology and the Zulu tribe of Africa.) Whatever the reason, the standard time reference, representing the time in Greenwich, England on the 24-hour scale, is commonly called Zulu Time.

Following the first world war, the impression was widespread in Germany that their armies had not actually lost the war, but had been "stabbed in the back" by disloyal persons within the country (primarily Communists, Freemasons, and Jews). The prestige of the legendary duo, Hindenburg and Ludendorff, somehow emerged from the debacle largely undiminished. After writing his memoirs in Sweden, Ludendorff returned to Germany in 1919, and began to preach a new "Nordic" religion, as well as vilifying all the internationalist groups that had stabbed Germany in the back. In the early 1920's he became associated with a former army corporal, Adolph Hitler, and the emerging Nazi party. (The word Nazi, of course, is a jargonization of Nationalsozialistische, the German word for "National Socialist".) Ludendorff even participated in Hitler's failed putsch in 1923, although subsequently he came to despise Hitler. Hindenburg, for his part, was elected President of the German Republic, in which capacity he was maneuvered into naming Hitler as chancellor. When Hindenburg died in 1934, Hitler succeeded him as President, assuming supreme command of the armed forces, while retaining the chancellorship. By the time of Ludendorff’s death in 1937, Hitler was the unchallenged dictator of Germany.

Is This a Prime?

Someone once asked me if 785645465756452 is a prime. Presumably the base of the representation is not 10, since otherwise the number is obviously a multiple of 2. On the other hand, we note that for any base, the number is not divisible by 3. Similarly, it cannot be divisible by 17, 23, 41, 47, 53, etc... regardless of what base is assumed.

It isn't too hard to show that 23 is the only (positive) base less than 100 for which the number is actually prime. The next bases for which the number is prime are 165, 189, 193, 345, 399, 455, etc.

Incidentally, converted from base 23 to base 10, the number is

Notice that each of the ten decimal digits 0,1,..,9 appears at least once in this number. In contrast, the original number has no 0, 1, 3, or 9, whereas it contains five 5s in the pattern xx5xx5xx5x5xx5x. The overall digit frequency is

Can we infer anything from this about how the original digits were selected?

A more interesting question is: Given an irreducible polynomial P(x) of degree > 0 with integer coefficients, does there necessarily exist an integer n such that P(n) is a prime? Of course, Dirichlet's Theorem states that there are infinitely many such n for any irreducible polynomial of degree 1. According to Ribenboim, the answer to the more general question is unknown. For most (irreducible) polynomials P(x) it's usually easy to find an integer n such that P(n) is prime, but for certain polynomials it's surprisingly difficult. For example, the least positive n such that n¹² + 488669 is prime is n = 616979.

It's also interesting to note that if exponential expressions are allowed, we can have no primes at all in certain sequences. For example, the number

is never a prime number (as can be proved by factoring the multiplier minus 1). See Richard Guy's Unsolved Problems in Number Theory for more examples.

A Two-Stage Lottery

Questions are frequently asked about the odds of winning a lottery, and it usually seems to be the same type of lottery, whether it's in the UK or in various US states. The player selects k distinct integers from the range 1 to N. Then the "house" randomly chooses k distinct numbers from the same range, and the player's winnings depend on how many of his numbers match the "house" numbers. Someone usually explains that the probability of matching j numbers is

where the binomial coefficient C(m,n) is defined as m!/(n!(m–n)!. Although this gives a pedagogically useful motivation for (and proof of) the elementary identity

it isn't a particularly challenging structure.

Suppose we drop the requirement for distinct integers. Let's say when we purchase a "chance" we are given five randomly selected integers from the range 1 to 45, duplications allowed. Then the house randomly selects five integers from the same range (again, duplications allowed). What is the probability of matching the house's multi-set of five numbers exactly? (Note that the order of selection is unimportant.)

This seems like a more interesting process because the result occurs in two stages. First, our personal numbers are selected and, although this doesn't determine whether we win or lose, the partition we draw determines our odds of ultimately winning. Ideally we would hope to get five distinct numbers, because that gives the best odds, whereas five of a kind gives the worst odds. Once every player has been given their five numbers, the house draws its numbers to actually determine the winner(s).

Whether this scheme has more popular appeal than the conventional method, it certainly is a bit more challenging to figure out the odds. The seven possible multi-sets (corresponding to the seven partitions of 5) are of the form

The product in the center column is the number of multi-sets with the respective pattern, without regard to order of selection. The right hand column gives the number of distinct sequences that give each of the occurrences of the respective multi-set.

Suppose we draw a multi-set of numbers with the partition "aabcd". Out of the 45⁵ possible selection sequences, there are (60)(595980) that give this partition, so our probability of drawing one of these is (60)(595980)/(45⁵). Then to actually win we need the house to get one of the 60 selection sequences that give our specific values of a, b, c, and d. So our odds of actually winning, given a multi-set of the form aabcd, are 60/(45⁵). The contribution of this multi-set pattern to our prior probability the product 595980(60)²/45¹⁰. The contributions of the other partition patterns can be computed in the same way, and the combined result is that our overall probability of winning is given by

Thus we have P = (5.81)10^–7. One of the nice things about answers to probability questions is that they immediately translate into combinatorial identities. The conventional lottery gives a summation for the binomial coefficient C(N,k), whereas the alternative scheme just described gives a summation for N^k.

Tables of 1 to N with Equal Columns

For any composite integer N = mn we can arrange the integers 1 to N in a rectangular array with m rows and n columns such that the sum of each individual column equals N(N+1)/(2n). Naturally if there are an even number of rows this is trivial, since we can simply list the numbers sequentially left-to-right on odd-numbered rows and right-to-left on even-numbered rows, such as the 2x3 table

However, with an odd number of rows (greater than 1) we need to use a slightly more subtle arrangement. We can still assign the numbers 1 through n (in order) to the first row, i.e., we set

The second row is assigned the numbers n+1 through 2n, placed consecutively beginning in the column just to the right of center, proceeding to the right-most column, and then continuing from the left-most column to the center. Thus we set

The third row contains the numbers 2n+1 through 3n. The number 2n+1 is placed in the middle column, and 2n+2 is placed in the right-most column. Then 2n+3 is placed just to the left of 2n+1, and then 2n+4 is placed just to the left of 2n+2, and so on, alternating until the row is filled. These assignments can be expressed as

Each column from k = 1 to (n+1)/2 has the following sum over the first three rows

whereas for the columns from k = (n+3)/2 to n the sums have the form

Thus every column sums to the same value, (9n+3)/2, over these first three rows. This leaves an even number of rows to be filled with the numbers 3n+1 to N, so these can be assigned consecutively in the usual pattern for pairs of rows. To illustrate this pattern, here are two tables for N = 35:

Is it always possible to construct a "primitive" m x n equal-column array, meaning that no subset of the rows form an equal-column array. We've seen that there are primitive EC arrays for 2 and 3 rows, but what about arrays with more than 3 rows?

Self-Descriptive Numbers and Auto-Valent Partitions

A well-known puzzle asks for a 10-digit integer whose first (i.e., most significant) decimal digit equals the number of zeros in the decimal representation of the integer, and whose second decimal digit equals the number of ones, and so on. This is sometimes called a self-descriptive number.

By construction, the sum of the digits equals 10, as does the sum of the products of each digit with its denomination. We see that the first digit must be at least 5, because six non-zero digits would yield a sum of products greater than 10. Letting d₀ denote the first digit, the number begins with d₀ and ends with d₀ zeros, which accounts for d₀ + 1 of the 10 digits. The remaining 10 – (d₀ + 1) digits, which are non-zero, must sum to 10 – d₀, so the sum is just one greater than the number of these digits. Hence all of these digits must be 1, except for a single 2. This implies that the number of 1’s must be 2, so there are three of these digits, consisting of 2, 1, 1. Consequently we have d₀ = 6, and the unique solution is 6210001000.

The same reasoning implies that, in every base B greater than 6, the only B-digit self-descriptive number is (B–4)B^B–1 + 2B^B–2 + B^B–3 + B³. This corresponds to the fact that the only auto-valent partition of N for N greater than 6 is N–4, 2, 1, 1, 0, 0, … 0. In general, the valences of a partition are just the numbers of distinct digits. For example, one of the partitions of 9 is 4+2+2+1, which we complete with zeros to give the canonical form 4,2,2,1,0,0,0,0,0. The valences count five 0’s, two 2’s, one 4, and one 1, which is written in canonical form as 5,2,1,1,0,0,0,0,0. Notice that the valences of this partition yield the very same partition, because we have five 0’s, two 1’s, one 5, and one 2, which gives (again) 5,2,1,1,0,0,0,0,0. We will refer to a partition with this property as auto-valent. The reasoning above proves that there is exactly one auto-valent partition for every integer greater than 6.

There is no self-descriptive B-digit number in the base B = 6 because there is no auto-valent partition of 6, basically because 6 – 4 = 2, which is not distinct from the 2 in the middle digits. However, it so happens that there is an auto-valent partition of 5, namely, 2,2,1,0,0, which corresponds to the self-descriptive number 21200. There are actually two auto-valent partitions of 4, namely 2,2,0,0, and 2,1,1,0, which correspond to the self-descriptive numbers 2020 and 1210 respectively. There are no auto-valent partitions of 3 or 2.

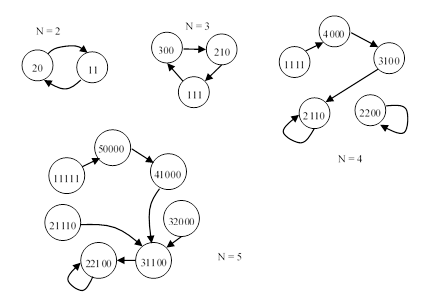
The figures below show the directed valence graphs for the partitions of N, with N = 2 through 5.

The graphs for N = 6 and 7 are shown below, with the partitions identified by letters assigned in descending numerical order.

The graph for N = 6 confirms that there is no auto-valent partition for that case, and the graph for N = 7 shows that J is auto-valent, and all the other partitions flow to the cycle FGH.

Return to MathPages Main Menu