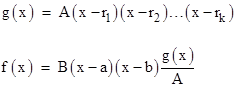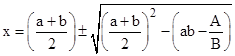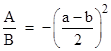|
Intersections of Polynomials |
|
|
|
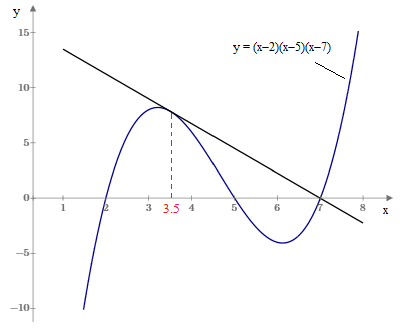
Given a cubic polynomial f(x) = (x−a)(x−b)(x−c) with 3 distinct real roots a,b,c, pick any 2 of those roots, say, a and b, and let. Then the line tangent to f(x) at u = (a + b)/2 passes through the point (c,0), as illustrated in the figure below. |
|
|
|
|
|
|
|
This is easy to prove, noting that the coefficient of xn−1 of a monic nth degree polynomial is the (negative) sum of the roots. If our tangent line is L(x) the cubic h(x) = f(x) − L(x) has a double root at u, so its three roots are u, u, q, whereas the three roots of f(x) are a,b,c. Since h(x) and f(x) have the same coefficient for x2, we have a+b+c = u+u+q. Then, since u = (a+b)/2, it follows that a+b = u+u and so q = c, which was to be proved. |
|
|
|
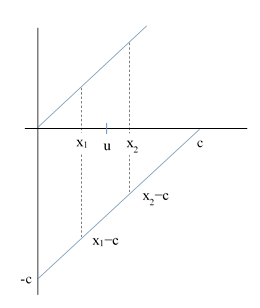
To give a slightly more "visual" geometrical explanation, notice that the proposition is actually a special case of the fact that for any real number v the line through the two points on the cubic at x1 = u−v and x2 = u+v passes through the x axis at c. (The particular case we started with corresponds to v = 0.) To visualize why this is so, notice that the quadratic polynomial g(x) = (x−a)(x−b) is just a parabola whose directrix is the vertical line bisecting the interval [a,b] at x = u. Since the parabola is symmetrical about this line, we have g(u+v) = g(u−v) for all v. Noting that f(x) = g(x)(x−c), we consider the line passing through the two points [x1, (x1−c)k] and [x1, (x1−c)k] where k = g(x1) = g(x2). The parameter k is just a scale factor that doesn't affect where the line crosses the x axis, so we need only consider the line through two points [x1, (x1−c)] and [x2, (x2−c)], as shown in the figure below. |
|
|
|
|
|
|
|
Since the two points are a distance c below the y = x diagonal, they obviously strike the x axis at c, as illustrated in the figure below. |
|
|
|
|
|
|
|
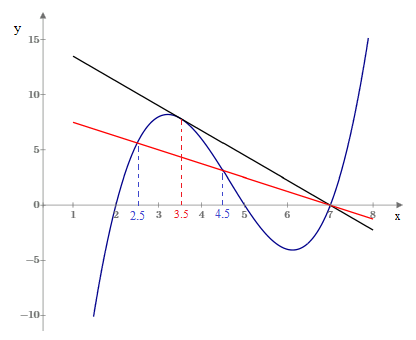
In the special case v = 0 the two points merge into one, and the direction of the tangent line is the limit of the chords as the points approach each other. |
|
|
|
The generalization to higher degrees is most easily made for the converse fact, i.e., if a straight line passing through the point (c,0) strikes the cubic (x−a)(x−b)(x−c) at two points, then the x coordinates of those two points are equidistant from (a+b)/2. Similarly, a vertical parabola passing through the points (c,0) and (d,0) strikes the quartic (x−a)(x−b)(x−c)(x−d) at two points whose x coordinates are equidistant from (a+b)/2. |
|
|
|
In general, the polynomials |
|
|
|
|
|
|
|
intersect when f(x) – g(x) = 0, which can be written as |
|
|
|
|
|
|
|
Thus the two points of intersection corresponding to the roots of the expression in square brackets occur at |
|
|
|
|
|
|
|
which shows that these two points of intersection are equidistant on either side of (a+b)/2, and the points coincide just if |
|
|
|
|
|
|