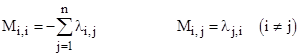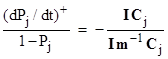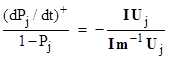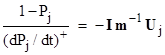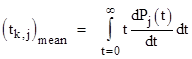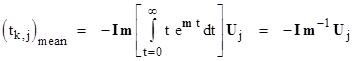Two Properties of Markov Models

The general equations of an n-state Markov model can be expressed in terms of matrices as MP = dP/dt where P is the column vector P = [P₁ P₂ ... P_n]^T and M is the n×n transition matrix with the components

The symbol λ_i,j signifies the exponential transition rate from state i to state j. This includes both failure rates and repair rates, and it allows for transitions in both directions between every pair of states.

For each j, let C_j denote the jth column vector of M, excluding the diagonal term M_j,j. Hence C_j has dimension n-1. This vector represents the transition rates from state j to each of the other n-1 states. We also define (dP_j/dt)⁺ as the rate of probability flow into state j.

Proposition: At steady-state conditions the quantity (dP_j/dt)⁺/(1-P_j) for any state j depends on the direction of C_j but is independent of the magnitude.

Proof: Let m denote the (n-1)×(n-1) matrix formed by deleting the jth row and column from the full transition matrix M, and let p denote the column vector formed by deleting the jth element from full state vector P. Then the equations of state give

Setting dp/dt = 0 for the steady-state condition and solving this equation for p gives

Now, letting I denote the identity row vector I = [1 1 ... 1] of dimension n-1, the conservation equation can be written as 1 - P_j = Ip. Hence, multiplying both sides of the above equation by I and substituting from the conservation equation, we have

We also note that for the steady-state condition (dP_j/dt)⁺ is equal to the rate of probability flowing out of state j, which is simply P_j I C_j. Consequently we have

The column vector C_j can be written as the product of a scalar magnitude and a unit vector U_j pointing in the direction of C_j. Making this substitution, the magnitude cancels out, and we are left with

Hence the left hand quantity depends on the direction of C_j, but not on the magnitude, which was to be shown.

Discussion: This proposition tells us that the steady-state "hazard rate" (the left hand quantity in the preceding equation) for any state j is independent of the overall rate of outflow from that state, but it does depend on how that outflow is distributed to the other states of the model.

Proposition: If the only non-zero component of C_j is λ_j,k, then for steady-state conditions the quantity (dP_j/dt)⁺/(1-P_j) is equal to the reciprocal of the mean time of transition from state k to state j.

Proof: In this case IU_j = 1, so the reciprocal of the hazard rate is

which is a scalar equal to the sum of the numbers in the kth column of m⁻¹. We wish to show that this equals the mean time of transition from state k to state j. To find an explicit expression for this mean time, it is most convenient to suppress the "return path" by setting λ_j,k = 0, and then begin with the initial condition P_k(0) = 1 and integrate the time from t = 0 to infinity, weighted according to dP_j(t)/dt, which is the probability density function for entry into state j. Hence the mean time is given by

Notice that setting λ_j,k equal to zero prior to solving for P_j(t) does not affect the time required for an object to transition from state k to state j, because this transition does not involve the return path from j back to k. Now, since we have suppressed the return path, the system equations are simply dp/dt = mp , which has the explicit dynamic solution

Notice that, since our initial condition is P_k(0) = 1, and state k is the exclusive return state from state j, the vector p(0) equals the vector U_j defined previously. We also have the conservation equation

Substituting into the mean time integral gives

which was to be shown.

Discussion: In retrospect the proof of this proposition is slightly superfluous, because it's essentially an immediate corollary of the previous proposition. Notice that the hazard rate of any state j is independent of the magnitude of the outflow rate from that state (by the previous proposition), so we can consider the limit as λ_j,k approaches infinity. In this limit the value of P_j approaches zero, so the hazard rate goes to (dP_j/dt)⁺, which is just the flow rate into state j (which also equals the flow rate out of state j). Also, it is stipulated that all the flow from state j goes to state k, so each element of the steady-state flow proceeds from state k to state j (by some route) and then immediately jumps back to state k to begin again. The steady-state flow rate (dP_j/dt)⁺ in the limit as λ_j,k approaches infinity is therefore the reciprocal of the mean time of transition from state k to state j. It follows from the previous proposition that, for any value of λ_j,k, the hazard rate (dP_j/dt)⁺/(1−Pj) equals the reciprocal of the mean time to transition from state k to state j, which was to be shown.

Return to MathPages Main Menu