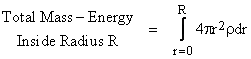Black Holes, Event Horizons, and the Universe

Is it conceivable that the entire universe is a "black hole"? To even begin to answer this question, we need clear definitions of "black hole" and "universe", neither of which are as easy to define as one might think. The formal definition of a black hole is a region of spacetime that is not in the causal past of the infinite future. If we combine this with any Robertson-Walker type universe, it's clear that neither an "open" infinite universe nor a "closed" finite universe can be considered a black hole, because the definition explicitly requires a black hole to be a proper sub-set of the overall universe, i.e., a black hole is defined as being excluded from some portion of the universe, so the universe itself cannot be a black hole according to this definition and with this class of "universes".

On the other hand, we're free to imagine "our universe" as a "closed" (though not necessarily finite) subset of some meta-universe that can be said to posses an "infinite future" of which our universe is not in the causal past, in which case by definition our universe is a black hole. Of course, this putative embedding may not be of the sort that is usually contemplated in the context of relativistic cosmologies, but this illustrates how much the answer to our original question depends on the precise definitions that we choose, as well as on whether we choose to imagine "our universe" as just a subset of some meta-universe.

It's also worth noting that (if we confine ourselves to just "our universe") not only does the formal definition of a black hole rule out the idea that a closed Friedmann universe is a black hole, it implies that a closed finite universe cannot even contain a black hole, because it has no infinite future. In other words, the formal definition of a black hole has no applicability at all in the context of a closed finite universe. Nevertheless, there are some conceivable configurations of matter and spacetime in a finite universe that could, with some justification, be called black holes, provided we are willing to adopt a more provisional definition. For example, one rough definition of a "black hole" is a mass whose Schwarzchild radius is outside of itself. If we can define all the terms adequately in the context of a finite universe, then we can agree to call such configurations "black holes", even though they do not (and cannot) satisfy the more formal definition.

If the average density of a region is r, then very roughly we could say the Schwarzchild radius of a spherical region in asymptotically flat spacetime (and neglecting gravitational binding energy, etc) of radius r is about 8πρr³/3. Therefore, regardless of the density, if we consider a spherical region (in flat space) of radius r greater than the cube root of 3/(8πρ) then the region would be called a black hole. However, this definition still doesn't apply to a closed Friedman universe because of two related effects: (1) the overall space has positive curvature on a cosmological scale (rather than being asymptotically flat), meaning that volume (and quantity of enclosed mass) increases more slowly with increasing radius, and (2) the entire space closes up on itself before reaching the radius that would constitute an event horizon. In a sense, this is almost the definition of a closed universe.

On the other hand, in an open infinite universe with overall negative curvature on a cosmological scale, volume increases with increasing radius faster than in flat spacetime, and there is no limit to the size of region we can consider. Therefore, we might think that for any fixed density there must exist regions large enough to be within their own Schwarzchild radii, so there would be actual cosmological event horizons, making vast regions of the universe inaccessible to each other. Inflationary cosmologies involve structures such as this, but such regions cannot really be regarded as "black holes" relative to each other. For one thing, the overall negative curvature of the universe in these models is inconsistent with the idea of the universe as a black hole. More fundamentally, we need to distinguish between the general notions of an event horizon and the boundary of a black hole. The definitions given in Wald may be paraphrased as follows

An asymptotically flat [and strongly asymptotically predictable] spacetime M is said to contain a black hole if not every point of M is contained in the causal past of future null infinity.

 The black hole region, B, of such a spacetime is defined to be the points of M not contained in the causal past of future null infinity. The boundary of B in M is called the event horizon.

These are often cited as the kind of precise and rigorous definitions needed to actually prove theorems about black holes, in contrast with more prosaic definitions such as

A black hole is a mass inside its own Schwarzschild radius.

Despite the extensive use of this formulation in (for example) the text of Hawking and Ellis (see Chapter 9), it has sometimes been claimed that this definition is "not actually used by any general relativist", because it depends on the ability to localize a quantity of mass, which is not well-defined in general relativity unless we make some assumption such as considering the mass to reside in an asymptotically flat spacetime. However, notice that Wald's definition is explicitly restricted to the very same class of spacetimes. As he says,

 ...we have defined the notion of a black hole only for strongly asymptotically predictable spacetimes [which are asymptotically flat by definition]...

 ... there appears to be no natural notion of a black hole in a "closed" Robertson-Walker universe which recollapses to a final singularity...

Thus, the range of possible universes for well-defined (in Wald's sense) black holes seems to closely coincide with the universes in which the total mass-energy of a system can be rigorously defined. They both evidently require an asymptotically flat universe. Of course, as Wald says,

 ... an approximate notion of a black hole still exists for any region of a closed Robertson-Walker universe that can be treated as an isolated system.

and in this same sense we can define the total mass-energy inside a radius R for a spherically symmetrical configuration of matter by the integral

According to Birkhoff's theorem the Schwarzschild solution is the essentially unique solution of the field equations outside a spherically symmetrical configuration of mass, whether static or not. In particular, there are no such things as spherically symmetrical gravitational waves, so there is no ambiguity about possible energy transfer across the boundary. This is, for example, the mass-energy that is used to establish the correspondence between the relativistic and Newtonian versions of Kepler's third law. On this basis, in a spherically symmetrical context, we can apply the "prosaic" definition of a black hole, but notice that we're now talking about "approximate notions of black holes", rather than precise and rigorous definitions. (It's unclear to what extent all the celebrated theorems about black holes are applicable to these "approximate black holes".)

Applying the prosaic definition in situations that do not possess spherical symmetry is even more difficult. We then have to give an invariant (i.e., coordinate-independent) definition of "inside the Schwarzschild radius" for a region that is not even spherical. We must also decide if we should use proper distance, and, if so, proper distance on what time slice? And so on. There's no doubt that giving a definition of black holes that's applicable to all possible local and cosmological contexts is difficult. For example, we can define a black hole as a region that's not in the causal past of future null infinity, but then we're likely to have trouble in a closed universe, since such a universe doesn't possess "infinity". Moreover, this prescription for a black hole has a certain tautological quality:

A black hole is that which is surrounded by an event horizon.

An event horizon is that which surrounds a region of no escape, i.e. a black hole.

In contrast, the "mass within its own Schwarzschild radius" prescription is of a different and, in a sense, more ambitious nature. It seeks to describe an actual physical circumstance that would constitute a black hole. Not surprisingly, people have only succeeded in doing this in a rigorous way for certain simplified cases, such as with spherical symmetry. No known definition of a black hole gives meaningful and unambiguous results for all possible contexts and, in particular, all possible cosmologies. Fortunately, stars, some galaxies, and even some cosmologies can be treated as spherically symmetric, so this special solution has a fairly wide range of applicability.

Another interesting point of definition concerns "event horizons". As noted above, Wald defines an event horizon as the boundary of the points of spacetime not contained in the causal past of future null infinity. However, Rindler defines an event horizon of any point P as the boundary between the region of points whose causal future includes P and the region of points whose causal future does not include P. Roughly, points that are more than c/H (where H is Hubble's constant) away from the point P are outside P's event horizon. If we imagine a spherical universe whose "circumference" exceeds c/H, then every point is on the event horizon of infinitely many other points.

So which is the "true" definition of an event horizon? Weinberg uses Rindler's definition. In fact, he credits Rindler with having coined the term "event horizon" [and "particle horizon"] in a 1956 paper. On the other hand, Misner, Thorne, Wheeler distinguish between two kinds of "horizons": (1) horizons in cosmology, and (2) horizons in black hole physics. The first correspond to Rindler's definition, and the second to Wald's. However, Misner, Thorne, Wheeler don't actually use the term "event horizon" for either of these concepts.

As an aside, it's interesting to note that when naive people first hear about black holes they often wonder: "If it takes infinite 'external time' for matter to collapse inside its Schwarzchild radius, and if there is only a finite amount of time in the entire existence of a closed universe, how can a true black hole exist?" The answer, of course, is that those naive people are right: a black hole (strictly defined) is inconsistent with a closed universe, precisely because of it's finiteness.

Return to MathPages Main Menu