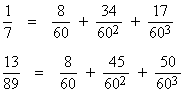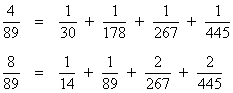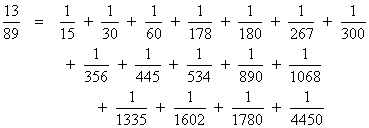|
Egyptian Unit Fractions |
|
|
|
|
|
|
|
The representation of rational numbers as sums of unit fractions dates back to the time of ancient Egypt. Today this subject survives mainly as a source of mathematical puzzles and problems in abstract number theory, but the subject is also of historical and anthropological interest, since it sheds light on the thought processes of people who lived at the very beginning of recorded human history. The discussion below focuses primarily on speculation as to the methods that may have been used by the ancient Egyptians to construct their tables. Articles concerning the purely number-theoretic aspects of unit fractions are contained in the Number Theory section of this site. |
|
|
|
|
|
1. The Rhind Papyrus 2/N Table |
|
|
|
One of the most puzzling episodes in the history of human thought is the 2000-year reign of Egyptian unit fractions. We can, at least in part, reconstruct the arithmetical manipulations involved, but the underlying reason or motive for expressing fractional quantities as sums of unit fractions remains mysterious. Was it simply a cumbersome style of writing that persisted for so many centuries just out of deference to traditional forms, or did it express an actual way of thinking that has since been forgotten? |
|
|
|
At the beginning of almost every general history of mathematics we find a description of how the ancient Egyptians operated with fractions almost exclusively in terms of unit fractions. For example, instead of saying 2/5 of my land was flooded, they would say 1/3 + 1/15 of my land was flooded. One of the earliest written records from ancient Egypt (transcribed circa 1650 BC from a source believed to date from around 1850 BC or earlier) is known as the Rhind Mathematical Papyrus, and contains a table expressing fractions of the form 2/n as sums of two, three, or four unit fractions with distinct denominators. The table covers 2/n for n up to 101, although the fractions with "even" denominators, e.g., 2/4, 2/6, etc, are omitted, showing that they clearly perceived the obvious equivalence of these with the reduced forms 1/2, 1/3, etc. |
|
|
|
The first entry in the table is 2/3, to which they assigned the expression 1/2 + 1/6. Every other table entry of the form 2/(3k) is assigned the expression 1/(2k) + 1/(6k), which suggests they consciously treated all denominators divisible by 3 as a single family, just as all denominators divisible by 2 were implicitly treated as a single family. |
|
|
|
Of the remaining table entries, the next is 2/5, to which they assigned the expression 1/3 + 1/15. All but one of the remaining denominators in the table that are divisible by 5 are assigned a simple multiple of this expression, i.e., for 2/(5k) they used 1/(3k) + 1/(15k). Similarly they assigned 1/4 + 1/28 to the table entry 2/7, and then "sieved out" all the remaining denominators divisible by 7 using expressions of the form 1/(4k) + 1/(28k). Finally, they assigned 1/6 + 1/66 to the table entry 2/11 and then used 1/(6k) + 1/(66k) for 2/(11k) with k = 5. |
|
|
|
The prime 11 seems to be where they stopped this procedure, which is consistent with that fact that the table extended only to denominators up to 101, so all the composites are sieved out by the primes less than 11. It's remarkable that the Egyptians of 1850 BC (and probably much earlier) had already developed this crude version of the "Sieve of Eratosthenes", and seemed to have a grasp of the difference between prime and composite numbers. Admittedly the sieve is not perfect, at least not according to our present understanding. For one thing, the number 55 should have been sieved out as a multiple of 5, but for some reason they chose to treat it as a multiple of 11. Also, the composite numbers 35, 91, and 95 were evidently not treated as composites, but were assigned unique representations. Nevertheless, the overall impression is very strong that they consciously sieved out the multiples of the smaller primes up to the square root of the largest denominator in the table, and then treated the remaining primes with unique representations. |
|
|
|
As we've seen, for each of the small primes 3,5,7,11 the Egyptians expressed 2/p as a sum of two unit fractions using the simple formula |
|
|
|
|
|
|
|
(The same formula also applies to the expression they assigned to 2/23, although it may be coincidental.) Once these primes, and their multiples, have been resolved, the table entries for the remaining prime denominators suggest that the Egyptians determined |
|
the representations by using the identity |
|
|
|
|
|
|
|
where "a" is some convenient “round” number greater than p/2. To find the remaining terms, we partition the quantity 2a - p into one, two, or three distinct parts such that each part is a divisor of a. (This is why it's good to choose a “round” number for a, so it has many divisors.) For example, with n = 89 we chose a = 60, which gives the difference 31. Thus, we need to express 31 as a sum of three or fewer distinct integers each of which divides 60. One such partition is 31 = 15 + 10 + 6, which leads to the representation that appears in the Rhind Papyrus for 2/89: |
|
|
|
|
|
|
|
On this basis, it's possible to summarize the 2/n table in the Rhind Papyrus by giving the values of a,b,(c,(d)) for each prime p such that 2/p = 1/a + 1/b + (1/c + (1/d)). These values are presented in the table below. |
|
|
|
TABLE 1: Summary of Rhind Papyrus 2/n Representations |
|
|
|
p 2a-p a b c d Also covers these |
|
--- ------ --- --- --- --- ------------------- |
|
3 1 2 6 all multiples of 3 |
|
5 1 3 15 25, 65, 85 |
|
7 1 4 28 49, 77 |
|
11 1 6 66 55 |
|
|
|
23 1 12 276 |
|
|
|
13 3 8 52 104 |
|
17 7 12 51 68 |
|
19 5 12 76 114 |
|
31 9 20 124 155 |
|
37 11 24 111 296 |
|
41 7 24 246 328 |
|
47 13 30 141 470 |
|
53 7 30 318 795 |
|
59 13 36 236 531 |
|
67 13 40 335 536 |
|
71 9 40 568 710 |
|
97 15 56 679 776 |
|
|
|
29 19 24 58 174 232 |
|
43 41 42 86 129 301 |
|
61 19 40 244 488 610 |
|
73 47 60 219 292 365 |
|
79 41 60 237 316 790 |
|
83 37 60 332 415 498 |
|
89 31 60 356 534 890 |
|
|
|
exceptional cases: |
|
|
|
35 25 30 42 |
|
91 49 70 130 |
|
95 25 60 380 570 |
|
101 1111 606 101 202 303 |
|
|
|
This table raises two obvious questions. First, assuming the Egyptians used something like formula (2) to determine their general unit fraction representations for 2/p where p is a "large" prime, how did they select the value of "a" and the partition of 2a - p from the available possibilities? Remarkably, if we examine all the possibilities, and limit ourselves to just the three and four-term representations where the smallest number x in the partition of 2a-p is greater than 1, then in most cases the expression appearing in the Rhind Papyrus is the one for which a/x is minimized. For example, the only possible solutions for p = 43 are |
|
|
|
partition of 2n-p |
|
p a 2a-p x y z a/x |
|
--- --- ----- ---- ---- ---- ----- |
|
43 24 5 2 3 12 |
|
43 28 13 2 4 7 14 |
|
43 30 17 2 15 15 |
|
43 30 17 2 5 10 15 |
|
43 36 29 2 9 18 18 |
|
43 42 41 6 14 21 7 |
|
|
|
and the representation appearing in the Rhind Papyrus is the one with a/x = 7. In all, the Egyptians used the solution with the minimum a/x for the "large" primes |
|
|
|
13, 17, 19, 29, 31, 37, 41, 43, 59, 67, 73, 79, 83, 97 |
|
|
|
whereas they missed it for the primes |
|
|
|
47, 53, 61, 71, 89 |
|
|
|
In these "missed" cases they missed the minimums by 2, 6, 1, 3, and 1 respectively. |
|
|
|
Another interesting fact that appears from a review of all the possible representations for each prime is that p = 29 is the first prime for which there is no three-term representation of 2/p (with the restrictions noted above). Thus, it's not surprising that 2/29 is the first entry in the Rhind Papyrus where a four-term representation is used. |
|
|
|
The second major question raised by Table 1 is how to explain the four exceptional cases. The first three are the composites 35, 91, and 95, that for some reason were not sieved out like the rest of the composites. From our point of view the case 2/95 = 2/(5*19) should have been sieved out by the small prime p = 5, giving it a representation of 1/(3k) + 1/(15k) with k = 19. Instead, we find that its representation was evidently based on the "large" prime p = 19, i.e., it is of the form 1/(12k) + 1/(76k) + 1/(114k) with k = 5. |
|
|
|
The cases 2/35 and 2/91 are even more unusual, and in a sense these are the most intriguing entries in the table. These are the only two composites whose representations are not simple multiples of the representations of one of their prime factors. Remarkably, in these two cases it appears the Egyptians reverted from the normal multiplicative decomposition to what might be called a "harmonic-arithmetic" decomposition. Recall that the ancient Greeks had definitions for various kinds of "means", including the |
|
|
|
|
|
|
|
It's believed the Greeks inherited these definitions from the Babylonians, but it's certainly possible they were also known to the Egyptians. In particular, the harmonic mean certainly looks Egyptian, given their affinity for unit fractions. In any case, notice that G(p,q) is not only the geometric mean of p and q, it's also the geometric mean of A(p,q) and H(p,q), which follows simply because |
|
|
|
|
|
|
|
In other words, AH gives an alternative decomposition of the composite number pq. This leads to the formula |
|
|
|
|
|
|
|
where of course the leading factor on the right is a unit fraction because p + q is even. This formula yields the Rhind Papyrus representations |
|
|
|
|
|
|
|
Thus we can say that every composite entry in the Rhind Papyrus 2/n table is based on a decomposition of n into its prime factors. In most cases the simple geometric factorization pq was used, but in two cases they used the arithmetic-harmonic factors AH. (As to why the numbers 35, 91, (and 95) might have been singled out for special treatment, see Appendix I.) This leaves only the final entry in the 2/n table, which is |
|
|
|
|
|
|
|
This entry could be constructed by formula (2) with a = 606 and the partition 1111 = 202 + 303 + 606, but it seems to stand out from the other table entries due to the fact that it's a simple multiple of 1/n. Perhaps this entry was just a formality, suggesting that for any n not covered in the table (i.e., larger than 100), we can use the four-term expansion |
|
|
|
|
|
|
|
so this effectively "completes" the table, allowing us to say that it provides a unit fraction representation of 2/n for all integers n. Interestingly, formula (4) can be seen as an illustration of the "perfectness" of the number 6, in the sense that the sum of the divisors equals double the number, i.e., 1 + 2 + 3 + 6 = 12 = (2)(6). |
|
|
|
In summary, the 2/n table of the Rhind Papyrus, which dates from more than a thousand years before Pythagoras, seems to show an awareness of prime and composite numbers, a crude version of the "Sieve of Eratosthenes", a knowledge of the arithmetic, geometric, and harmonic means, and of the "perfectness" of the number 6. This all seems to suggest a greater number-theoretic sophistication than is generally credited to the ancient Egyptians. Whether they originated these ideas or borrowed them, perhaps from the Babylonians, is unclear. (We shouldn't overlook the possibility that the Babylonians borrowed them from the Egyptians.) |
|
|
|
|
|
2. The Akhmin Papyrus |
|
|
|
One relatively late document on Egyptian unit fractions is known as the Akhmin Papyrus, apparently written around 400 AD. Considering that the material in the Rhind Papyrus dates from 1850 BC (or earlier), this shows that the use of unit fractions persisted for a remarkably long time. It appears that by the time the Akhmin Papyrus was written there was a fairly sophisticated criterion for the selection of the table entries. To expand N/P, check the smallest solutions where exactly k denominators are divisible by P using the congruences |
|
|
|
k congruence modulo P |
|
---- ------------------------------ |
|
1 Na = 1 |
|
2 Nab = a + b |
|
3 Nabc = ab + ac + bc |
|
4 Nabcd = abc + abd + acd + bcd |
|
|
|
with 0 < a < b < c < d, and take the one with the smallest maximum value. For example, to find the best expansions of n/17 we have the following choices for (a,b,c,d): |
|
|
|
n k=1 k=2 k=3 k=4 |
|
--- ----- ----- ------- -------- |
|
2 (9) (3,4)* (2,5,6) (1,2,3,6) |
|
3 (6) (4,5) (1,3,4)* (1,2,5,6) |
|
4 (13) (3,8) (1,4,5)* (1,2,3,7) |
|
5 (7) (2,4)* (2,3,5) (1,2,5,7) |
|
6 (3)* (1,7) (1,2,4) (1,2,3,5) |
|
7 (5) (1,3)* (3,4,7) (1,4,5,6) |
|
8 (15) (1,5)* (2,4,6) (2,3,5,6) |
|
9 (2)* (3,6) (3,4,5) (1,2,4,6) |
|
10 (12) (1,2)* (1,3,6) (1,3,4,5) |
|
11 (14) (3,7) (2,3,4)* (1,2,4,7) |
|
12 (10) (2,6) (2,4,5) (1,2,3,4)* |
|
13 (4)* (3,5) (1,2,6) (1,2,4,5) |
|
14 (11) (1,4)* (1,3,5) (2,3,4,6) |
|
15 (8) (2,3)* (1,2,7) (2,4,5,6) |
|
16 (16) (2,5) (1,2,3)* (1,5,6,7) |
|
|
|
The asterisks mark the solutions with the smallest maximum term. The remarkable thing is that the asterisks also mark the expansions of n/17 appearing in the Akhmin Papyrus. It's a perfect match. Clearly whoever wrote that papyrus was organizing the solutions in |
|
a way that is consistent with the method described here. |
|
|
|
Applying this same analysis to the n/19 table in the Akhmin Papyrus gives the results |
|
|
|
n k=1 k=2 k=3 k=4 |
|
--- ----- ----- ------- -------- |
|
2 (10)+ (4,6)* (1,5,6) (1,2,3,6) <--- |
|
3 (13) (2,8) (3,4,5)*+ (1,3,6,7) |
|
4 (5)+ (2,3)* (1,2,8) (1,3,4,5) <--- |
|
5 (4)+ (1,5) (1,2,3)* (2,3,5,6) <--- |
|
6 (16) (1,4)*+ (4,5,6) (2,3,4,6) |
|
7 (11) (2,6)*+ (2,4,7) (1,4,5,6) |
|
8 (12) (6,7) (2,3,5)*+ (1,2,4,7) |
|
9 (17) (4,5) (2,3,4)*+ (1,2,3,5) |
|
10 (2)*+ (3,6) (1,4,5) (1,2,3,4) |
|
11 (7) (1,2)*+ (1,3,6) (1,3,4,7) |
|
12 (8) (1,7) (2,4,6)*+ (1,2,5,6) |
|
13 (3)*+ (1,8) (4,6,7) (2,3,4,5) |
|
14 (15) (1,3)*+ (3,5,6) (1,4,6,7) |
|
15 (14) (2,4)*+ (1,2,5) (1,3,5,6) |
|
16 (6) (4,7) (1,2,4)*+ (1,3,4,6) |
|
17 (9) (3,5)*+ (1,4,7) (4,5,6,7) |
|
18 (18) (3,4)*+ (1,3,5) (1,3,7,8) |
|
|
|
The expansion with the smallest max denominator is indicated by an asterisk, and the one appearing in Akhmin is indicated by a plus sign. In this case the match is nearly perfect, with just the following three exceptions |
|
|
|
fraction Akhmin Expected |
|
------- --------- ------------------ |
|
2/19 10' 190' 12' 76' 114' (Rhind) |
|
4/19 5' 95' 6' 38' 57' (2*Rhind) |
|
5/19 4' 76' 6' 19' 38' 57' (2*Rhind+ 1/19) |
|
|
|
In these three cases the Akhmin author selected the expansion with the fewest terms, rather than the expansion with the smallest max denominator. Interestingly, the "expected" series for 2/19 is precisely the one that appears in the Rhind Papyrus, and of course the series for 4/19 is just twice 2/19 (in Akhmin as well as in the expected series), and the expected series for 5/19 is just 1/19 plus 4/19. |
|
|
|
Even granting that the selection criterion for the Akhmin tables was as described above, this still leaves the question of what algorithm might have been used to compute the results. It occurs to me that the author of the Akhmin Papyrus could have used a "meta-table" to construct his tables. (Maybe he kept the meta-table secret for job security?) Basically there are only a limited number of combinations of coefficients, so we could build a meta-table just once and use it to construct all the individual n/p tables. |
|
|
|
Meta-Table For Ahkmin Papyrus Unit Fractions |
|
|
|
A B a b c d A B a b c d |
|
--- --- - - - - --- --- - - - - |
|
2 1 2 5 1 5 |
|
2 3 2 1 20 9 5 4 |
|
3 1 3 15 8 5 3 |
|
6 5 3 2 10 7 5 2 |
|
3 4 3 1 5 6 5 1 |
|
6 11 3 2 1 60 47 5 4 3 |
|
4 1 4 40 38 5 4 2 |
|
12 7 4 3 20 29 5 4 1 |
|
8 6 4 2 30 31 5 3 2 |
|
4 5 4 1 15 23 5 3 1 |
|
24 26 4 3 2 10 17 5 2 1 |
|
12 19 4 3 1 120 154 5 4 3 2 |
|
8 14 4 2 1 60 107 5 4 3 1 |
|
24 50 4 3 2 1 30 61 5 3 2 1 |
|
40 78 5 4 2 1 |
|
|
|
To find the best unit fraction expansion of n/p, all we need to do is take the first A,B from this table such that nA-B is a multiple of p. For example, to expand 12/17 we try the first entry, A = 2,B = 1, which gives 12A-B = 23, not a multiple of 17. So we try the next entry, A = 2,B = 3. This doesn't work either, so we go on to the next. The first entry that works is the 14th: A = 24,B = 50. Therefore, the optimum expansion of 12/17 is given by [a,b,c,d] = [4,3,2,1]. |
|
|
|
In this case the solution was given by the 14th entry in the meta-table. If we check all the n/17 expansions in the Akhmin Papyrus we find that the solutions are given by the meta-table entries listed below: |
|
|
|
n -> 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
entry # -> 8 12 22 9 3 5 19 1 2 11 14 7 10 4 6 |
|
|
|
Using this method the hardest expansion to find would be 4/17, because we have to check down to the 22nd entry in the meta-table (A = 20,B = 29), but it isn't particularly laborious. With a little practice we could probably do it in our heads. (Notice that we can take A and B modulo p, so the 22nd entry with p = 17 is equivalent to A = 3, B = 12, and obviously 4(3) - 12 = 0.) Actually to cover all of the n/19 expansions they would have needed a meta-table going up to the 6's. (I've just shown it up to the 5's.) |
|
|
|
|
|
3. Why Unit Fractions? |
|
|
|
Why did the ancient Egyptians (and others) persist in their use of Egyptian fractions for so many centuries? Was it a conceptual limitation, or simply a matter of notation? Some scholars contrast the exactness of Egyptian expansions with the approximate nature of fixed-base expansions such as in decimal system and the Babylonian sexigesimal system. This contrast is interesting, although it takes some effort for modern readers (accustomed to fixed-base representations) to imagine the intellectual difficulties involved in this paradigm shift. |
|
|
|
The Egyptian preference for exact expansions reminds me of the Greek preference for geometry over symbolic arithmetic. When the Greeks discovered irrational numbers they realized that rational arithmetic can only approximate the values of most real numbers. As a result, not wanting to deal with approximations, they devoted themselves mainly to geometry. Even within geometry, their insistence on being able to give exact constructions using straight-edge and compass is similar to the Egyptian insistence on giving exact expansions using unit fractions. |
|
|
|
It’s also interesting to compare the fixation on unit fractions with the insistence of ancient astronomers on resolving the motions of celestial objects into perfect circles – a practice that, like the use of unit fractions, also persisted up to the 1500s. In both cases it seems to have become a self-justifying end in itself. We resolve numbers into unit fractions and we resolve motions into circles because those are (respectively) the only “perfect” forms, even though the basis of these concepts of “perfection” was not closely examined, and even though there was no noticeable benefit in going through the contortions necessary to resolve things into these (supposed) a prior forms. |
|
|
|
There are at least two separate aspects to Egyptian fraction expansions that makes them puzzling to modern people. One is the variable "base", e.g., rather than expanding a fraction into a sum of fractions with the denominators equal to powers of a single base number (such as 10 or 60), they freely chose denominators to give an exact identity. Thus, while the Babylonians might have expressed 1/7 as (approximately) |
|
|
|
|
|
|
|
the Egyptians would have preferred the exact expansion |
|
|
|
|
|
|
|
This also highlights the other puzzling aspect of Egyptian fractions, namely, their preference for unit numerators. This might have derived from their "binary" approach to integer arithmetic, in which successive doublings of the operands were used to multiply numbers, so that effectively their numbers were expressed in the form |
|
|
|
|
|
|
|
where the coefficients ci are either 0 or 1. When they expanded their arithmetic to include fractions, they might have sought to express all numbers in the form |
|
|
|
|
|
|
|
where again the coefficients ni are either 0 or 1, but realizing that using Dj = 2-j would not allow exact expansions, they used independently variable denominators. |
|
|
|
Still, it isn't clear what purpose was served by the Egyptian unit fractions. Presumably one of the basic motivations for expanding rational fractions is to enable the comparison of different quantities. For example, if someone offers us 1/7 of a bushel of corn and someone else offers us 13/89 of a bushel, which should we take? The Babylonian approach would be to express the two numbers in sexigesimal as |
|
|
|
|
|
This makes it easy to see that while the first terms are identical, the second term of 13/89 is larger than the second term of 1/7. In fact, it's clear that the fraction 13/89 exceeds 1/7 by about 6/602 + 33/603. This shows the value of expressing fractions in a fixed-base system: it enables us to immediately assess the relative magnitudes of different quantities (and the difference between them) by placing them on a common basis. |
|
|
|
However, the Egyptian approach doesn't seem to serve this purpose. One possible Egyptian expansion of 1/7 is 1/14 + 1/21 + 1/42, but how would they expand 13/89? Using a "binary" approach, they might have considered first expanding the numerator into powers of 2 as follows |
|
|
|
|
|
|
|
Then from a table of 2/n expansions they would find |
|
|
|
|
|
|
|
which immediately gives |
|
|
|
|
|
|
|
The 1/89 term in the expansion of 8/89 could be combined with the 1/89 in the original expansion to give 2/89, for which we could substitute the 2/n table expression above. The terms 2/267 and 2/445 could be written as (1/3)(2/89) and (1/5)(2/89) respectively, so again we could substitute from the 2/n table expression. Adding up these terms would |
|
give |
|
|
|
|
|
|
|
This gives a complete unit fraction expansion for 13/89, but it isn't obvious how this facilitates a comparison with 1/14 + 1/21 + 1/42. At some point, they would need to place the two numbers on a common denominator. |
|
|
|
Of course, we don't actually know how the ancient Egyptians would have expanded 13/89, since the tables that have survived don't include any general rules. Possibly they had some way of expanding the first few terms on specified denominators for purposes of comparisons, but there is no evidence of this. Based on the examples they gave, we would expect them to expand 13/89 into something like |
|
|
|
|
|
|
|
or perhaps, to minimize the largest denominator, the might have used |
|
|
|
|
|
|
|
but this still gives no easy basis of comparison with some other fraction, such as 1/7 = 1/14 + 1/21 + 1/42. The most expedient way of comparing the magnitudes would be to simply cross-multiply to clear the fractions, finding that (13)(7) = 91 exceeds (1)(89) = 89, but again there is no evidence the ancient Egyptians looked at it this way. |
|
|
|
Although, there are undeniably several interesting algebraic patterns in the historical Egyptian expansions, the purpose of those expansions (i.e., the function they served) remains unclear. Were they just exercises in manipulation, or did they serve some useful purpose? How did the Egyptians compare the sizes of two general fractions? How did they add, subtract, multiply, and divide general fractions? Did they use the 2/n table for anything? Some scholars have suggested that the partitioning of estates might have been one motivation, and it’s easy to see that this might have given the Egyptians a special interest in unit fractions, but it’s not clear what benefit they got from expressing unit fractions as sums of other unit fractions. |
|
|
|
It's interesting to consider other possibilities, such as gambling. The modern theory of probability originated in a series of letters between Fermat and Pascal on the subject of partitioning the stakes of an unfinished game of chance. I'm no scholar of ancient cultures, but I'd be willing to bet that the ancient Egyptians practiced some forms of gambling. Maybe some forgotten predecessors of Fermat and Pascal were concerned about the same thing, and worked out a set of mathematical techniques for dealing with these kinds of partitions. Still, I can't quite see how to make use of Egyptian unit fractions for any of these purposes. |
|
|
|
One possible reason the practice of expressing numbers as unit fractions endured for so long is the limitations of notation. Darrah Chavey points out that the ancient Egyptians wrote a number 1/n as the number n with an oval above it. This is just a single-variable symbol, and doesn't readily accommodate the two variables needed to express the ratio of an arbitrary numerator and denominator. It is necessary to devise a completely new notation. Moreover, not only is a new notation required, it may have been difficult for them to imagine a single quantity with two variable and independent arguments. They could adjoin unit fractions by addition, but couldn't conceptually consolidate them into a single entity. |
|
|
|
Searching for clues to explain the motives behind the use of unit fractions, we might examine the Rhind Papyrus itself. Recall that Ahmes poses the problem of dividing 3 loaves of bread equally between 5 people. Naturally each person gets 3/5 of a loaf, but there are multiple distinct ways of partitioning the loaves to accomplish this. One way would be to cut each loaf into five equal parts and give each person three parts. This would require 12 cuts. Another way would be to make one cut in each loaf, dividing it into 3/5 and 2/5 parts, and give each of three people one of the 3/5 parts. This leaves three parts of size 2/5. One of these could be cut in half, and each of the remaining two people could be given a 2/5 and a 1/5 slice. This would require only 4 cuts. |
|
|
|
In the book "Ancient Puzzles", Dominic Alivastro suggests that Ahmes might have wanted to solve this problem by cutting one loaf into five equal slices, and the other two loaves each into three equal slices. Then take one of the 1/3 loaf slices and cut it into five equal slices. Each person could then be given his share in the form |
|
|
|
|
|
|
|
Alivastro suggests that this might be more readily perceived as equable than the partition 3/5, 3/5, 3/5, (1/5 + 2/5), (1/5 + 2/5), although it must be said that the uniform partition into congruent shares (1/5 + 1/5 + 1/5) would presumably be even more obviously equable. Both of these partitions requires 12 cuts, so we cannot prefer one over the other based on economy of cuts. |
|
|
|
Overall the most plausible explanation for the ancient fixation on unit fractions seems to be that they had difficulty conceiving of a single quantity in terms of two variables (numerator and denominator), and were looking for simple "whole" fractional quantities. Just as the "whole" natural numbers are those of the form n/1, it was natural to imagine that the "whole" fractional numbers are of the form 1/n. |
|
|
|
|
|
Appendix I: Why Were 35, 91, and 95 Treated Differently? |
|
|
|
It's intriguing to consider the following table: |
|
|
|
Double-Triangular and Related Numbers |
|
|
|
k T = (k+2)(k+3) Q = 6k+1 T-Q TQ |
|
--- -------------- ---------- ------ ----- |
|
1 12* 7 5 35 |
|
2 20* 13 7 91 |
|
3 30* 19 11 209 |
|
4 42* [25] 17 |
|
5 56* 31 [25] |
|
6 72 37 (35) |
|
7 90 43 47 |
|
8 110 [49] 61 |
|
9 132 (55) (77) |
|
10 156 61 (95) |
|
11 182 67 |
|
12 210 73 |
|
13 240 (85) |
|
14 272 (91) |
|
15 306 97 |
|
16 342 103 |
|
18 420 109 |
|
|
|
Notice that the values of TQ less than 100 are precisely those that are treated by arithmetic-harmonic decomposition in the 2/n table. Also, I've placed parentheses around the composite values in the Q and T-Q columns, with square brackets to indicate squares. Notice that the numbers 35, 91, and 95 appear, as do the corresponding values of 2a-p, namely, the squares 25, 49, and 25 respectively. Also, the number 55 appears, which was treated in a slightly unusual way in the 2/n table by being sieved out by the larger of its two divisors, rather than the smaller. The only other composites in these columns are 77 and 85, which don't seem to have been treated in any unusual way in the 2/n table. By the way, the numbers in the T column, which are double-triangular numbers, seem to have been favorite choices for "a". Each value marked with asterisk was used in the 2/n table as an "a" value at least once. |
|
|