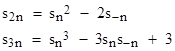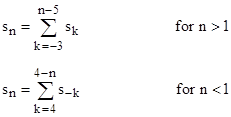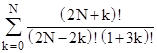Perrin's Sequence

Define the sequence of integers by the linear recurrence formula

with the initial values s₀ = 3, s₁ = 0, s₂ = 2. This sequence was discussed by Edouard Lucas in 1878 (American Journal of Mathematics, vol 1, page 230ff), who noted that if p is a prime then p divides s_p. This is an immediate consequence of Fermat's Little Theorem, and as such is a necessary but not sufficient condition for primality (see proof). Subsequently (1899) the same sequence was mentioned by R. Perrin (L'Intermediaire Des Mathematiciens). The most extensive (published) treatment of this sequence was given in an excellent paper by Dan Shanks and Bill Adams in 1982 (Mathematics of Computation, vol 39, n. 159). Shanks and Adams referred to this as Perrin's sequence.

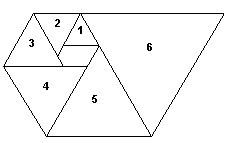
This sequence has many interesting properties, making it, in some ways, more remarkable than the Fibonacci sequence. For example, most people are familiar with the spiral of equilateral squares whose edge lengths correspond to the Fibonacci numbers, but less well-known is the spiral of equilateral triangles shown below described in Spiral Tilings and Integer Sequences.

The edge lengths of successive triangles in this spiral satisfy the Perrin recurrence s_n = s_n–2 + s_n–3 as well as the recurrence s_n = s_n–1 + s_n–5, as is apparent from the above figure. This can be seen as a consequence of the fact that the characteristic polynomial of Perrin's sequence, x³ – x – 1, is a divisor of the characteristic polynomial of the 5th order sequence, i.e.,

The real root r of x³ – x – 1 has the nice expression as a sequence of nested cube roots:

If we define the angle θ in terms of this root r as

then the terms of the Perrin sequence can be expressed in closed form as

In fact, with the appropriate provisos, we can replace n with any complex argument z to define Perrin's function on the complex plane, as shown in the figure below for real components from –5 to 15 and imaginary components from –5 to +5.

White indicates regions where both the real and imaginary components are positive, black where both are negative, and the two shades of gray where one is positive and the other negative. The zeros of this function are all on the real axis in the left half-plane, whereas there are two sets of complex conjugate zeros on the right half-plane (at points where all four shades meet).

Obviously, for any positive prime p and any integer n we have

so in particular we have

In addition, for any integers m,n,k we have the relation

Which is really just a special case of a much more general class of relations satisfied by any linear recurring sequence. (See the note Identities for Linear Recurring Sequences.) In this particular case we have relations like

and so on, as well as

Using these relations for s_2n and s_2n+1 gives an efficient means of computing s_k via the usual binary pattern algorithm on the plus and minus sides of the sequence. This same two-sided approach can be extended to higher order recurrences, but it quickly becomes more practical to use the more general one-sided relations (described in the note mentioned above).

Perrin's sequence also has the interesting property that its terms are cumulative sums of the sequence itself, i.e., we have s₁ = 0 and

The terms of Perrin's sequence can also be expressed as a function of binomial coefficients, leading to many interesting results. For example, it's possible to deduce that the summation

is an integer for N=2755452, and for no smaller N. (See the note Summations and Recurrences.)

As a compositeness test, Perrin's sequence is much stronger than the typical 2nd order Lucas sequence. For example, the smallest symmetric pseudoprime relative to the Fibonacci quadratic x² – x – 1 is 705, whereas the smallest relative to Perrin's cubic x³ – x – 1 is

as found by Shanks and Adams (using an HP-41C calculator). Subsequently Shanks, G. Kurtz, and H. Williams tabulated all the symmetric pseudoprimes relative to Perrin's sequence less than 50(10)⁹. They noted that none of these pseudoprimes had the signature of a prime p such that Perrin's polynomial is irreducible (mod p). As far as I know the question of whether such a pseudoprime exists is still open.

Further discussion of pseudoprimes relative to various polynomials can be found in the notes

Pseudoprimes for x^2 - 4x - 9

Lucas and Perrin Pseudoprimes

Symmetric Pseudoprimes

Return to MathPages Main Menu