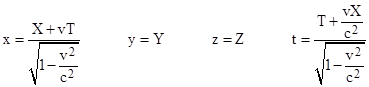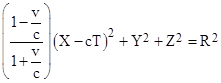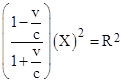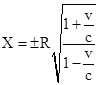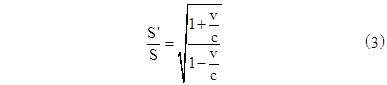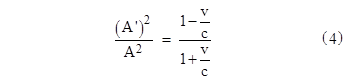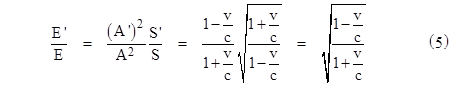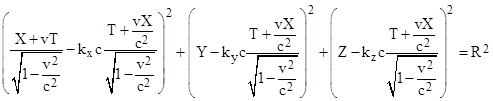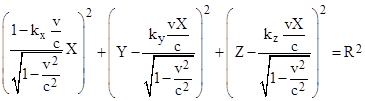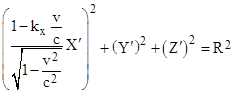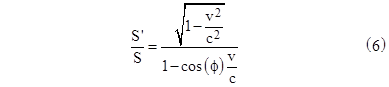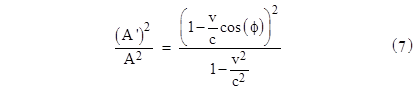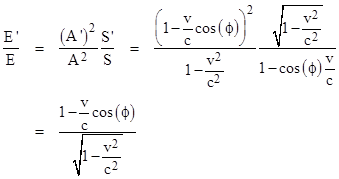The Aarau Question and the Light Complex

There is an interesting connection between Einstein’s earliest thoughts about special relativity and his 1905 paper.  Between October 1895 and early fall of 1896 he attended school in Aarau, Switzerland, preparing for the entrance exam at the ETH in Zurich.  In his last autobiographical notes, published in 1956, he recalled:

During that year in Aarau the question came to me: If one runs after a light wave with light velocity, then one would encounter a time-independent wavefield. However, something like that does not seem to exist! This was the first juvenile thought experiment which has to do with the special theory of relativity.

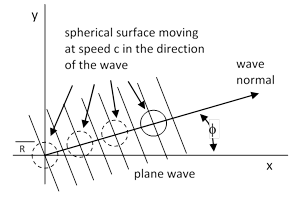
Ten years later, in Section 8 of his 1905 paper, he essentially presents this same thought experiment in his derivation of the formula for the transformation of the energy of a “light complex”.  He considers a plane wave of light, and imagines the part of this wave enclosed within a spherical region of constant radius R whose center is moving at the speed of light in the same direction as the wave. Letting k_x, k_y, k_z denote the cosines of the angles between the wave normal and the x, y, and z axes respectively, the equation of the surface of this moving sphere is

This is depicted in the figure below, showing the sphere’s position at four different times as it moves along with the plane wave.

Now, just as he did in 1895, Einstein considers the properties of the light complex contained within the co-moving sphere. Obviously no energy crosses the surface, because the surface is moving at the speed of light in the same direction as the plane wave. Thus the energy contained within this moving spherical surface is constant, equal to the energy density of the wave multiplied by the volume S = (4/3)πR³ of the sphere.

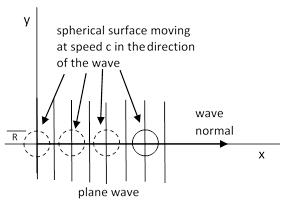
In the special case when the wave normal is parallel to the x axis we have k_x = 1, k_y = 0, and k_z = 0, so the equation of the spherical surface reduces to

In this special case the sphere moves along the x axis as shown below.

Now consider this same moving surface in terms of inertial coordinates X,Y,Z,T moving in the positive x direction with speed v. According to the Lorentz transformation we have

Making these substitutions into (2), we get the equation for the moving surface in terms of the transformed coordinates

This represents an ellipsoid moving in the positive X direction at the speed of light. It is elongated in the X direction by the reciprocal of the square root of the leading factor, as can be seen from the fact that at Y = Z = T = 0 the value of X satisfies

and therefore

The volume of the enclosed region is increased by the same factor as the X extent, so the ratio of the volume of this ellipsoid to the volume of the original sphere is

Now, Einstein had already shown in Section 7 of his paper that the ratio of the energy densities relative to the two frames of reference, for the special case when the plane wave is moving parallel to the x axis, is equal to the ratio of the squared amplitudes of the waves, which in this special case is

Therefore, the ratio of the total energy of the light complex contained within the surface relative to the two frames of reference in this special case is

More generally, if we return to equation (1) for a plane wave propagating in an arbitrary direction characterized by the direction cosines k_x, k_y, and k_z, the equation of the spherical surface in terms of the X,Y,Z,T coordinates moving with speed v in the x direction is

Hence the surface locus at T = 0 has the equation

To evaluate the spatial volume enclosed within this surface (in terms of the X,Y,Z,T coordinates), it’s useful to notice that a space coordinate transformation of the “shear” form

for any constant α and β preserves volume, as is evident from the fact that the determinant of the transformation matrix is unity. (For a simpler example of this, consider a two-dimensional shear transformation X′ = X, Y′ = Y + αX, which preserves the areas of plane figures, since the area of a triangle depends only on the altitude and the base, not on the lateral location of the apex.) Therefore, the volume within the surface described by the above equation equals the volume within the surface described in terms of X′,Y′,Z′ by

By definition k_x = cos(ϕ) where ϕ is the angle between the wave normal and the x axis, so the ratio of the volume of this ellipsoid to the volume of a sphere of radius R is

Of course, if ϕ = 0 this reduces to equation (3). Now, in the previous section of his 1905 paper, Einstein had derived the general form of the ratio of energy densities as

which of course reduces to (4) when ϕ = 0. Combining this with the ratio of volumes, we get Einstein’s general ratio between the energies of the light complex in terms of the two systems of reference

This of course is exactly the same as the ratio of the frequencies ν′/ν of the light complex in terms of the two systems of reference. Einstein called this coincidence “remarkable”, although he didn’t explicitly link it to the fundamental relation E = hν that he had proposed for light quanta just weeks before in his 1905 paper on the photo-electric effect. Obviously that relation would have been incompatible with relativity if energy and frequency did not transform in exact proportion to each other. From this point of view, establishing the identity between the laws of transformation for the frequency and the energy of a “light complex” was one of the most significant results of Einstein’s relativity paper. It’s interesting that it emerged from consideration of the Aarau question, i.e., from examining the characteristics of a light wave within a volume moving along with the wave at the speed of light. In his Autobiographical Notes written in 1949 he wrote about his search for a universal formal principle that he had become convinced was needed (in 1905) to lead us to assured results.

After ten years of reflection such a principle resulted from a paradox upon which I had already hit at the age of sixteen: If I pursue a beam of light with velocity c (velocity of light in a vacuum), I should observe such a beam of light as an electromagnetic field at rest though spatially oscillating. There seems to be no such thing, however, neither on the basis of experience nor according to Maxwell’s equations… One sees that in this paradox the germ of the special relativity theory is already contained. Today everyone knows, of course, that all attempts to clarify this paradox satisfactorily were condemned to failure as long as the axiom of the absolute character of time, or of simultaneity, was rooted unrecognized in the unconscious. To recognize clearly this axiom and its arbitrary character already implies the essentials of the solution of the problem.

As far as I know, the Autobiographical Notes of 1949 was the first time Einstein mentioned this early thought experiment from 1895, and he repeated essentially the same account to Selig (quoted at the beginning of this article) in 1954. It’s interesting that he never mentioned it in any of his many previous recollections describing his path to special relativity. This is strangely reminiscent of Newton’s “falling apple” story, which Newton never mentioned prior to the last couple of years of his life, when he apparently described it to several people, including his niece Catherine Barton, who passed the story along to Voltaire. The most authoritative source is Stukeley, who dined with Newton in 1726 and reported on their after-dinner conversation:

The weather being warm, we went into the garden and drank tea, under shade of some apple trees, only he and myself. Amidst other discourses, he told me, he was just in the same situation, as when formerly, the notion of gravitation came into his mind. It was occasion'd by the fall of an apple, as he sat in contemplative mood. Why should that apple always descend perpendicularly to the ground, thought he to himself. Why should it not go sideways or upwards, but constantly to the earth's center.

Conduitt, who married Catherine Barton, gave a similar account, placing the incident in a garden near Newton’s mother’s house in Lincolnshire in 1666.

Einstein might have mentioned his youthful paradox in the introduction of his 1905 paper, describing his motivations, but apparently by that time he was more impressed by the “asymmetries not inherent in the phenomena”. Nevertheless, Section 8 of the paper clearly shows the outcome of a thought process trying to grasp the attributes of light by considering a “light complex” contained within a surface co-moving with the light.

Return to MathPages Main Menu