The Longitude of Lewis and Clark

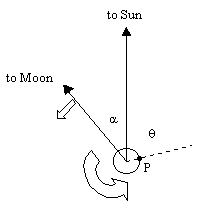
When Lewis and Clark made their famous journey across North America in 1804 one of their objectives was to establish the latitude and longitude of various landmarks along the way. However, they didn't have accurate clocks, so it was necessary to make use of coordinated astronomical sightings. Specifically, they needed to make simultaneous readings of the positions of the Sun and and Moon, making careful note of the date as well. From this information it is possible to determine the longitude by comparing these readings with observations taken at Greenwich, England. To see how this works, suppose at high noon on a particular date at Greenwich the positions of the Sun and Moon are as shown below.

Throughout we will refer only to the angles along the ecliptic, making allowances for the differing lattitude. At this instant the Sun is directly "above" Greenwich, and the Moon is "lagging" behind the Sun by an angle α. For a hypothetical traveller at location P on the Earth's surface it is still early morning at this instant. It will be high noon at location P a few hours later, once the Earth has rotated through the angle θ. At that time the angle α between the Sun and Moon will have increased slightly, because of the Moon's orbital motion around the Earth.

To compute the value of θ from the observed change in α, we need to know the rate of the Earth's rotation, the orbital rate of the Earth around the Sun, and the orbital rate of the Moon around the Earth. Notice that if the Earth didn't rotate and if the Moon's absolute angular position relative to the Earth didn't change, then both the Sun and Moon would appear to have a retrograde rotation around the Earth with a period of one year due to the Earth's orbital motion around the Sun. This motion has an angular velocity of

This is just 360/T where T is the sidereal year consisting of 365d 5h 48m 45s. The angular velocity of the Earth's rotation is

This is just 360/T where T is the sidereal day consisting of 23h 56m 4.098s. Lastly, the angular velocity of the Moon's orbit around the Earth is

based on the sidereal month consisting of 27d 7h 43m 11s. With these speeds, we can determine that the time required to reach high noon at location P is

In that length of time the Moon's position as seen from the Earth will not have moved quite as far, due to the motion of the Moon, so the different between the angular positions of the Sun and Moon will have increased by the amount

Eliminating Δt from these two equations, we get

The angle θ represents the longitude of P relative to Greenwich, so if the angle between Sun and Moon is measured at high noon at the observatory in Greenwich on a particular date, and the angle is measured on that same date at some other location, we can determine the longitude of that other location by seeing how much their angles differ. Of course, if the reading at location P is taken when the Sun is past high noon by an angle ϕ, then we must subtract ϕ from the result given by the above formula. If we define increasing a as positive, then the general formula is

Incidentally, the word "Zulu" is common parlance for "ZL", which is short for Zero Longitude, referring to Greenwich, England.

Notice that we've used the sidereal (inertial) measures for all the angular speeds. For example, we used the month equal to 27.3217... days. The synodic month is about 1/12th longer than this, because by the time the Moon has gone once around the Earth, the Earth has gone about 1/12 of the way around the Sun, so in order to re-align with the Earth and Sun, the Moon must go this additional distance. In effect, the apparent rate of the Earth's orbit around the Moon is ω_month - ω_year. Hence we have 360/(ω_month - ω_year) = 2551443 sec, which is the synodic month of 29d 12h 44m 3s.

Return to MathPages Main Menu