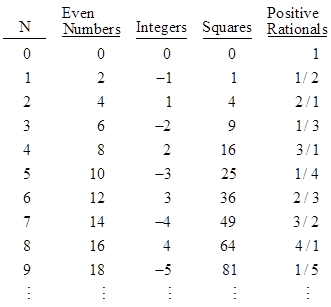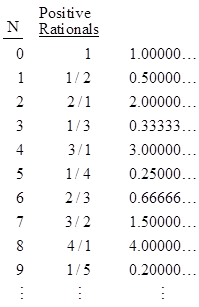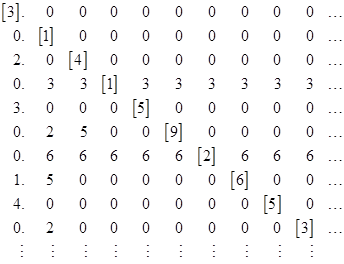Cantor's Diagonal Proof

Simplicio: I'm trying to understand the significance of Cantor's diagonal proof. I find it especially confusing that the rational numbers are considered to be countable, but the real numbers are not. It seems obvious to me that in any list of rational numbers more rational numbers can be constructed, using the same diagonal approach.

Salviati: This is a common question, Simplicio, and a good one to ask when you first hear about Cantor's diagonal proof. No one can claim to understand the proof unless they can explain clearly why it works for reals and not for rationals.

A set of objects is said to be countably infinite if the elements can be placed in a 1-to-1 correspondence with the integers 0, 1, 2, 3, .. Some examples of countably infinite sets are illustrated below

In each case we can show that every element of the set appears exactly once in the list. You mentioned that you were particularly interested in the rational numbers. The pattern we've chosen is to take k = 1, 2, 3, ... and for each value of k list all the fractions n/d with n + d = k and gcd(n,d) = 1, in increasing order of n. Most people are fairly satisfied that each rational number will appear exactly once on this list. (Note that the ordering we've chosen is not unique, but a single successful ordering is enough to prove that it can be done.)

Now your question is, if we list the rationals in the form of decimal expansions, and apply Cantor's diagonal argument, won't we construct another rational number that is not contained in the above sequence? If so, we would have a contradiction, and something would be seriously wrong somewhere.

Fortunately, the diagonal argument applied to a countably infinite list of rational numbers does not produce another rational number. To understand why, imagine you have expressed each rational number on the list in decimal notation as follows

As you know, each of these numbers ends in an infinitely repeating finite sequence of digits. For example, 1/7 = 0.142857 142857 142857 and so on. Conversely, if the decimal representation of a number does not eventually turn into a repetition of a finite sequence of digits, then (by definition) it's not a rational number. (It's important to keep this in mind.)

Now, let's apply Cantor's procedure to an infinite list of rational numbers. There are many different ways we can choose the digits of this new number, the only requirement being that the number must differ in at least one decimal place from each number on the list. (There's also a technical requirement to avoid any of the alternate decimal representations of numbers, because for example 1 = 0.9999... but we won’t dwell on that.) The digits of our new number are shown in square brackets on the diagonal

So our new number starts out as 3.141592653... (Incidentally, we could continue to choose the digits of π along the diagonal until reaching 4/13, which is the 83^rd fraction on the list. For more on this, see Interfering With π). The point is that in order to prove that we have constructed a new rational number we need to prove that the number on the diagonal eventually falls into a pattern of a repeating finite string of digits. Without being able to prove this, all we can say is that we've produced a new number that was not on the original list, but we can't claim to have produced a new rational number.

Now you might wonder, given the fact that we have quite a bit of free choice in selecting the digits of our new number, if we couldn't somehow choose the digits so that they do eventually repeat. After all, every number of the original list eventually repeats in a finite number of digits, so why can't our "sidestepping" repeat with a period equal to the least common multiple of all the finite periods of the rational numbers on the list?

The answer to that question is the key to the entire discussion. The digits of every rational number repeat after some finite number of digits, so the "period" of every rational number is finite. However, there is no upper bound on the period of rational numbers, i.e., the periods are all finite, but there is no largest period. Thus, in a manner of speaking, the least common multiple of this set of strictly finite things is infinite. So there's really no hope that our diagonal digits will have a finite period. From this we conclude that our original listing of the rationals that seemed to include all of them, really does include all of them. Cantor's diagonal argument has not led us to a contradiction.

Of course, although the diagonal argument applied to our countably infinite list has not produced a new rational number, it has produced a new number. The new number is certainly in the set of real numbers, and it's certainly not on the countably infinite list from which it was generated. This applies to any countably infinite list that contains at least all the rational numbers: the new number we produce will be a real and irrational number. From this we conclude, perhaps surprisingly, that no countably infinite list of numbers can include all the real numbers. It was from this that Cantor realized it's possible to speak meaningfully about different kinds of infinities.

Various philosophical objections can be (and have been) raised against this kind of reasoning. Some mathematicians gone so far as to deny the "existence" of irrational numbers, and it's certainly true that this kind of reasoning about infinities eventually leads to results that are genuinely counter-intuitive, if not actually paradoxical (such as the Banach-Tarski Theorem), but it hasn't been shown to be internally inconsistent.

Simplicio: You said there is no upper bound on the size of natural numbers, and thus the least upper bound on the naturals is infinite, even though every natural number is finite. To me this implies that there can be numbers which do not have such a bound. Is that not so?

Salviati: It sounds like you're trying to invent a kind of "number" that has infinitely many digits in the direction of geometrically increasing significance, somewhat analogous to the reals, which have infinitely many digits in the direction of geometrically decreasing significance. Number systems like what you are talking about have actually been developed, Simplicio, (see p-adic numbers) but the crucial difference is that the infinite sequence of digits is in the direction of increasing, not decreasing, significance, so the resulting implied "sum" does not converge to a value that behaves consistently like a magnitude. (The valuations are said to be "non-Archimedean".) There's nothing wrong with conceiving new forms of numbers like this, but we need to be clear about how they differ from other forms of numbers.

Simplicio: Irrational numbers, such as the square root of 2, are suggested as, in the number of digits in their decimal expansion, not having this bound. I suggest that it reflects a misunderstanding of infinity to believe that such numbers can be exactly represented by an infinite decimal expansion, since the existence of numbers with such expansions is purely hypothetical, and that it is better to say that such numbers can only be closely approximated by a finite decimal expansion.

Salviati: You're certainly free to admit into your mathematics only those things that you see fit, Simplicio. However, limiting yourself to only magnitudes whose decimal expansions are finite is a somewhat arbitrary restriction. Many magnitudes have infinite expansions in base 10 (such as 1/3 = 0.33333....) whereas they have finite expansions in some other base (e.g., 1/3 = 0.1 in base 3). This might lead you to modify your restriction to allow only magnitudes whose expansions are, in some sense, definable. For example, even though there are infinitely many digits in 0.33333.... we know clearly the "rule" that determines what those digits are, so we accept the completed infinity of digits, even though we can't type them all out. But if you use this as your criterion, then you are hard pressed not to accept √2 as an acceptable magnitude, because we also know the "rule" for determining those digits. Admittedly the "rule" is much simpler in the case of 0.33333...., so you might try to restrict your "acceptable magnitudes" based on the complexity of the rule.

Overall, it sounds like you're trying to define a class of numbers that includes the rationals plus all the irrational magnitudes that have some acceptably simple definition. You would then call this overall set "the real numbers", and assert that Cantor's diagonal argument does not apply (because any acceptably simple definition is presumably one of at most a countably infinite set of definitions). You would be right in asserting that your set of numbers has the same cardinality as the integers, but you would be better advised not to call them "the real numbers", so as to avoid confusion with a set that has previously been postulated by other people on somewhat different premises. Think of a new name for your set of numbers, and call yourself a constructivist, and most of your critics will leave you alone.

Simplicio: Cantor's diagonal proof starts out with the assumption that there are actual infinities, and ends up with the conclusion that there are actual infinities.

Salviati: Well, Simplicio, if this were what Cantor had done, then surely no one could disagree with his result, although they may disagree with the premise. What he actually did was somewhat more ambitious, and quite a bit more interesting. He started with the assumption of actual infinity and ended up showing that this implies more than one kind of infinity! Again, you may disagree with the premise, but given the premise his conclusion follows, and it is really quite an interesting conclusion.

Return to MathPages Main Menu