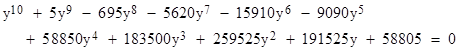|
Quintisection of an Angle |
|
|
|
One of the most famous geometrical constructions in Euclid's "Elements" is to divide a line segment in "extreme and mean ratio" (Book VI, Prop 30) or, equivalently, to divide a line segment into two parts a,b such that a rectangle with sides a+b and b has the same area as a square of size a2 (Book II, Prop 11). Such a figure is often called a "golden rectangle. Obviously by equating (a+b)b to a2 we have the equation ab + b2 = a2, and if we divide both sides by b2 this gives x + 1 = x2 where x = a/b. The roots of this equation are |
|
|
|
|
|
|
|
One of the many interesting properties of r is that it is the ratio of a diagonal to a side of a regular pentagon. Thus it allows us to construct a regular pentagon and quintisect a circle. |
|
|
|
We can also construct a right triangle with hypotenuse 1
and sides of length (1/r) and |
|
|
|
|
|
|
|
Letting T denote tan(β/5), we have the identity |
|
|
|
|
|
|
|
We've defined tan(β) as the quantity |
|
|
|
|
|
|
|
so if we square both sides of the above equation, multiply by 2, add 1, and square again, and make the substitution x = T2, we arrive at |
|
|
|
|
|
|
|
Now we only need to prove that this polynomial neither factors nor decomposes into quadratics. From elementary Galois theory we know that if a given number is constructible by Euclidean methods, then the degree of its minimum polynomial with rational coefficients is a power of 2. Thus, if the minimal polynomial with root equal to the given number is not a power of 2, it follows that the number is not constructible by Euclidean means. (Note that the converse of this theorem is not true, because it's actually possible to have a number whose minimal polynomial is of degree 2n but which cannot be constructed.) |
|
|
|
If β/5 could be constructed, then tan(β/5)2 could also be constructed, and this magnitude is a root of the 10th degree polynomial given above. To prove that it is the minimum polynomial for that magnitude, make the substitution x = y + 2, which gives |
|
|
|
|
|
|
|
By Eisenstein's criterion this is irreducible, so the minimum polynomial over the rationals with root tan(β/5)2 has degree 10, which is not a power of 2. Therefore, β/5 cannot be constructed by Euclidean methods. |
|
|
|
This is exactly similar to the method of proving that an arbitrary angle cannot be trisected by Euclidean means. The ancient Greeks sought a way of trisecting any angle, but since π/3 is constructible this would imply that we could construct the magnitude w = 2cos(π/9), which is a root of p(x) = x3 - 3x - 1. We know this is the minimum polynomial because if we make the substitution x = y + 1 we have p(y) = y3 + 3y2 - 3, which is irreducible by Eisenstein's criterion. Thus the degree of the minimum field extension of 2cos(π/9) over the rationals is of degree 3, which is not a power of 2, so it cannot be constructed by Euclidean methods. |
|
|
|
Notice that in both examples we had to perform a substitution of variables into the polynomial to bring a it into a form where Eisenstein's criterion applies. I don't know of any systematic way of finding the right substitution, other than trial and error. This raises an interesting question: If a polynomial p(x) is irreducible over the rationals, does there necessarily exist a bi-linear change of variables, i.e., x → (ay+b)/(cy+d) such that the resulting polynomial in y satisfies the conditions of Eisenstein's criterion? Also, assuming p(x) is irreducible, how many substitutions would we expect to try (in some natural order) before finding one that works? Also, what is the analog of Eisenstein's criterion for testing primality of integers? |
|
|