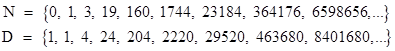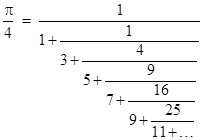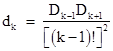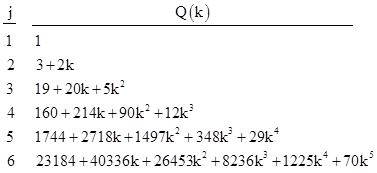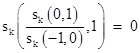Integer Sequences Related To π

For any given integers s₀ and s₁ we can construct the infinite sequence s_n, n = 0, 1, 2, ...  generated by the recurrence

For example, with the initial values s₀ = 0, s₁ = 1 we produce the sequence

On the other hand, if we take the initial values s₀ = 1, s₁ = 0 we produce the sequence

For convenience, let s_k(m,n) denote s_k based on the initial values s₀ = m and s₁ = n.  The two sequences listed above can serve as the "basis" for all sequences of this form, according to the relation

The ratios of corresponding terms in these sequences approach some interesting values.  For example, we can show that for any integers m,n (positive or negative)

Simply dividing two general expressions of this form, we get the more general relation for any w,x,y,z

This applies to any real values of w,x,y,z, not just integers, so it gives the limit of ratios of terms of any sequence s_k(x,y) to terms of the sequence s_k(w,z).  To illustrate, note that the sequence s_k(1,1) has the values

and the sequence s_k(-2,1) has the values

The ratio of the 9th terms of these sequences is

If we add 2 to this ratio and multiply by 4/3 we get 3.141593...  Another interesting observation concerns the growth rate of the individual sequences.  It appears that the difference in consecutive ratios of consecutive values approaches 1 + √2.  In other words, for any given initial values, we have

It would be interesting to determine an explicit solution of the recurrence (1), which is a simple homogeneous linear 2nd-order recurrence, but with non-constant coefficients.

Since (3) shows that all the sequences are easily related, it's enough to consider just the ratio of two sequences.  Define the integer sequences D_k and N_k such that both satisfy the recurrence relation (1) with the initial values N₀ = 0, N₁ = 1 and D₀ = 1, D₁ = 1. Thus the values of N and D are

It can be shown that the ratio N_k/D_k equals the kth convergent of the continued fraction for the inverse tangent of 1:

Incidentally, this continued fraction can also be inferred from the fact that

The continued fraction can be converted into the following infinite series

where the kth term c_k is just the difference between the (k–1)th and the (k+1)th convergent of the continued fraction.  In other words

As a result, the partial sums of the series are just the sums of two consecutive convergents of the continued fraction. Clearly the sequence of numerators is just the odd numbers. Is there a simple way of characterizing the denominators? In that regard, notice that if we let g denote the greatest common divisor of 

it follows that

and

where d_k is the denominator of the kth term in the above series for π/2.  Now it appears that

so g = [(k+1)!]², which implies that

Equation (5) is a kind of convolution of the terms of the two sequences, which may be a more natural definition of their relation than the original linear 2nd order recurrence.

Actually (5) is just one of a set of formulas relating the "cross-products" of these two series.  In general we have

where Q(k) is a polynomial in k of degree j–1.  The first few such polynomials are listed below

The constant coefficients are just the values of the N sequence, whereas the leading coefficients 1, 2, 5, 12, 29, 70, ... are the "Pell numbers" that satisfy the recurrence p_n = 2p_n–1 + p_n–2. Also, notice that the sums of the coefficients for the jth polynomial are 1, 5, 44, 476, 6336, 99504, ...  which are the values of the other "basis sequence" mentioned previously. In other words, these values satisfy the same recurrence as do the N and D sequences, but with the initial values 1,0,...

Incidentally, using the original sequence notation, we have the identity, applicable to any linear second-order recurrence:

This is discussed in the note on anti-symmetric arrays for linear recurrences.

Return to MathPages Main Menu