The Ordering of Interactions

It's often noted that our experience consists entirely of interactions rather than isolated objects, but that nevertheless we persist in encoding and visualizing our experience in the form of a space of usually-isolated objects that occasionally interact. This fictitious way of conceptualizing our experience certainly seems to be efficient in most ordinary circumstances, but it may contribute to the difficulties we encounter when trying to make sense of elementary physical operations.

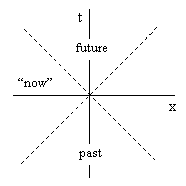
As an example, consider the notion of causality and the "ordering" of events. In terms of our fictitious image of isolated objects we consider that each individual object induces a partitions of spacetime into three distinct regions, past, "now", and future, bounded by null cones as shown below

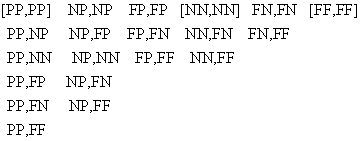
In contrast, if we take fundamental quantum interactions (rather than particles) as the primitive elements of our model, then each interaction induces a partition of spacetime into six distinct regions. Letting P, N and F denote Past, Now, and Future respectively, the six regions are

where, for example, FP signifies the Future of one end of the interaction and the Past of the other end. Of course the two "ends" of a typical fundamental interaction are very close together, both spatially and temporally, so the "mixed" regions NP, FP, and FN are usually vanishingly small. Thus when dealing with most common macroscopic events it makes sense to just focus on the three pure regions PP, NN, and FF. This allows us to treat the causal orderings of interactions as if they have same general 3-part structure as the ordering of our fictitious isolated objects.

Observe that, if we restrict our attention to just the pure regions PP or FF we encounter no surprises relating to causality, correlations, etc. in quantum mechanics. By this I mean that if two interactions are located entirely within each others future/past respectively, then there are no ambiguities about the "flow" of events, and quantum mechanics does not predict anything outside the ordinary expectations of causality. When dealing with elemental interactions (i.e., interactions that cannot be broken down into sub-interactions) we find counter-intuitive results only when the interactions are not well-ordered, in the sense of each interaction being wholly within the future or the past of the other.

If we focus on the possible relations between just two interactions, there are 20 distinct ways in which they could be causally "ordered" (in contrast to just 3 ways for two discrete particles). These 20 "orderings" correspond to the ways in which the two ends of one interaction can be placed in the six regions induced by the other:

All of our ordinary macroscopic experience is with sets of interactions that are of the three types shown in square brackets. In fact, due to the large value of the speed of light, our experience is almost all with the "well-ordered" relations [PP,PP] and [FF,FF]. We know what to expect in those cases, and quantum mechanics agrees with our expectations. The surprising and seemingly "paradoxical" results of quantum mechanics involve interactions that relate to each other in one of the 17 "mixed orderings" or the [NN,NN] ordering, where our experience with well-ordered interactions is not applicable.

In my view, when people talk about locality being violated by quantum mechanics, they are applying a notion of "locality" based on fictitious isolated objects, whereas our experience actually consists of irreducible (quantum) interactions which have a more complicated set of possible orderings and causal relations.

It's interesting that both relativity and quantum mechanics extended our notions of the possible order-relations between instances of experience. Relativity, by the finiteness of the speed of light, expanded the classical relation "simultaneous" from an infinitesimal slice of spacetime to the entire region of spacetime outside the null-cones associated with any two events. Quantum mechanics, by the irreducibility of fundamental quantum interactions, induces a more complicated set of possible order-relations between the basic constituents of experience.

The most common objection to this view is that by replacing "particles" with "interactions of finite spatial and temporal extent" as the fundamental constituents of experience, we are basing our ontology on inherently "non-local" entities, so it no longer makes any sense to talk about locality at all. However, it can be shown that quantum interactions actually are local, provided the measure of "nearness" is taken to be absolute spacetime separation. (There is really no choice about this if we want our concept of locality to be based on a measure of nearness that is invariant under Lorentz transformations.) This is because quantum interactions act entirely on null-cones, which is obviously true of electromagnetic interactions, and it's also true of all other quantum interactions, as Dirac noted: the relativistic Schrödinger wave propagates along null-cones.

Of course if we focus only on the pseudo metric structure of spacetime and the implicit null paths connecting every pair of points, it's tempting to slide down the reductionist slope into thinking that the entire manifold degenerates trivially into a single locus of "co-local" points. On this basis some people conclude that the absolute spacetime interval cannot serve as the measure of nearness in any meaningful definition of locality. However, this view fails to take account of the fact that the irreducible element of experience is not the point particle but the quantum interaction. Each interaction does indeed reduce to a single co-local entity within the pseudo metric of spacetime, but distinct interactions do not reduce to a single interaction. Thus, the (highly non-trivial) structure of experience arises jointly from the pseudo metric structure of spacetime - with its finite velocity of light - and the irreducibility of finite quantum interactions.

Unfortunately, this all begs the question of what exactly constitutes an "elemental" interaction. The problem with treating interactions (rather than particles) as elemental is that it isn't obvious how to define "interaction" without first defining the entities that are doing the interacting. This is really just another way of stating the well-known problem of separating the observer from the observed, and what it means for systems to be "isolated" from each other. I think we can't avoid a relative definition of elemental, by which I mean that an interaction that is elemental relative to me may be compound relative to you.

There's an interesting parallel here to the absence of absolute simultaneity in special relativity. Does the lack of absolute "elementality" lead to logical contradictions? As far as I can tell, it doesn't. For example, relative to Schrödinger’s Cat the outcome of the experiment is a result of compound interactions, all following in a sequence of small and well-ordered interactions. However, relative to an observer isolated from the Cat's environment the overall interaction is elemental. Schematically it looks like this

Accordingly as "you" take the upper or lower branch, the interaction between points A and D is compound or elemental. The point of this distinction is that it determines how those interactions may be related, either causally or by correlation, to other interactions according to their full "order" in spacetime.

It may seem strange that a given large-scale interaction must be treated as elemental for one observer but compound for another. Our intuition says that two events either are or are not connected by an elemental interaction, but this is similar to our intuition that two events either are or are not simultaneous, i.e., it stems from a failure to recognize that elementality (like simultaneity) can only be properly defined operationally, and on that basis it need not be absolute. This all suggests that each connected subset of the set of all interactions can be regarded as a system, and the elementality of every other interaction with which a system comes into contact is determined relative to that system. On that basis, the causal influences and correlations follow from the full spacetime ordering of those interactions.

Return to MathPages Main Menu